

深入了解WinDaq导数算法
描述
导数是一种数学工具,用于从任何给定函数获取变化率。当要微分的函数表示为方程时,我们将应用适当的导数公式以类似的方程格式获得变化率。当函数为波形时,可以使用称为微分放大器的电子设备来计算输入信号的导数。结果是第二个波形,可以记录、数字化或以其他方式用于提供有关原始波形的其他信息。
在基于计算机的仪器环境中,通过将波形通过软件中构建的导数函数传递波形,可以区分先前记录到磁盘的波形。后一种方法有几个优点。与硬件差异化器不同,软件差异化器是无漂移的,从而提高了精度和可重复性。对生成的差分波形进行自动校准,以输入波形除以秒为单位。最后,当硬件解决方案生成一个要么接受,要么离开的导数信号时,软件差异化器允许通过在同一或不同通道上执行多个导数操作来增强灵活性。每个操作都可以有自己的一组参数,为波形分析提供有价值的“假设”方法。
本应用笔记旨在使用DATAQ Instruments的高级CODAS分析包的衍生实用程序作为其模型,探索基于软件的波形微分的复杂性。本文中讨论的波形微分的所有元素都包含在该产品中。
差异化和集成基础知识
分化和整合之间的关系是如此密切,以至于讨论一个自然会导致对另一个的讨论。这些强大工具的一个更基本的应用是单位转换。例如,假设我们正在从汽车获取以英尺/秒 (ft/sec) 校准的速度波形。利用这个信号,我们可以确定汽车在整个测试过程中任何瞬时点的速度。可以肯定的是,有用的信息。但假设我们对车辆的加速度感到好奇。换句话说,我们想要速度波形相对于时间的变化率。此类信息由导数函数通过将以英尺/秒为单位校准的波形转换为以英尺/秒/秒或英尺/秒 2 校准的波形来提供。同样,我们可以选择对速度波形进行积分,以得出位移的度量。在此操作之后,单位从英尺/秒转换为(英尺/秒)×秒,或简称为“英尺”。
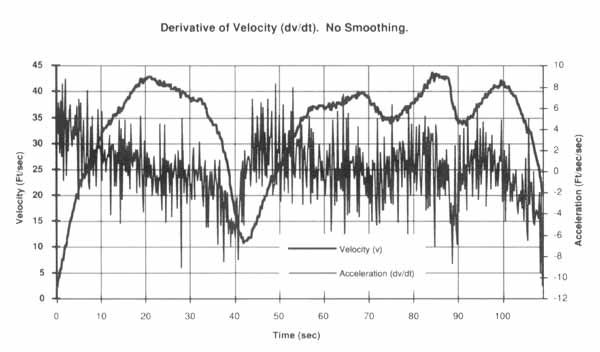
图 1— 应用导数函数而没有平滑的好处会产生噪声结果,几乎没有提供有关输入波形真实变化率的信息。
生成微分波形
再次回到我们的示例速度波形和我们对推导加速度的需求,我们可以确定任何给定范围内速度的变化,并除以经过的时间以获得粗略的近似值。但这是一种繁琐的波形微分方法,很容易导致错误,并且无法提供加速度的整体图形图像,以帮助我们识别其他感兴趣的区域。这些问题可以通过软件差异化来解决。此类产品可用于导出波形的一阶导数的最基本方法是计算速度波形上任何给定点与下一个相邻样本之间的差异。然后将此差值除以将两点分开的经过时间增量,以产生以ft/sec 2或加速度为单位的变化率。这种方法的问题在于结果非常嘈杂,如图1所示,图1模拟了这种差异化方法。现实世界的信号总是有一个噪声分量,随着微分过程的放大。虽然图1中的速度波形看起来相当无噪声,但得出的加速度波形实际上毫无用处。正如模拟微分器提供可选的低通滤波器一样,软件微分器也必须提供对生成的波形进行平滑处理的方法。存在许多平滑方法,但最好的方法是将平滑与派生函数相结合,从而提高软件执行效率。最小二乘算法满足此要求。
应用于线性回归的最小二乘法是一种众所周知的技术,用于推导形式的预测方程。
y = mx + b
来自随机抽样的组。从基本微积分中,我们知道这个方程的一阶导数(dy/dx)产生m,即直线的斜率或变化率。出于微分目的,截距量 (b) 没有意义,因此无法计算。有了这些基本信息并将最小二乘线性回归模型应用于定义采集波形的连续点,我们可以为定义这些点的最佳拟合线构建一个方程,其中线的m或斜率表示线在用于计算的波形值上的平均变化率。进一步扩展此推理,如果我们改变计算回归线的点数 (n),我们可以调整应用于计算变化率的平滑程度。n值越高,平滑越大,值越低平滑越少。

图 2— 通过计算由采样值组成的重叠线段的斜率生成导数波形。
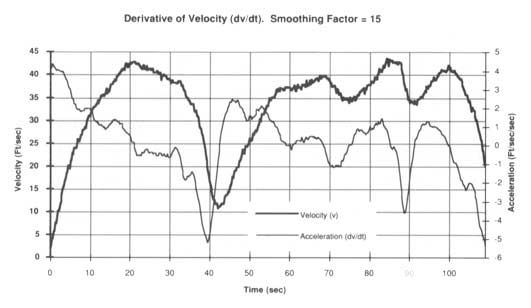
图 3— 对微分波形进行平滑处理可以显著提高其可读性。这里,平滑因子 15 应用于图 1 所示的相同导数函数。
图 2以图形方式演示了如何将回归模型应用于由y 表示的波形数据点。该示例使用平滑因子 3,这意味着每个线段的斜率 (m) 是通过 3 个连续波形值计算的。请注意线段计算中存在的重叠,它在差分波形中产生的点数与函数y 表示的波形中存在的点数相同。图3是将回归方法应用于图1相同速度波形的结果。计算每条回归线的点数为 15,从而产生生成的加速度波形中显示的显著平滑程度。
图 4是WinDaq 播放实用程序中打印屏幕的复制品。顶部波形是从在测试轨道上运行的汽车获得的速度。底部波形是一个计算的通道,加速度,它是通过速度的一阶导数得出的,平滑因子为 15。
其他波形差分问题
在选择分析包来执行波形微分时,应考虑许多问题。首先,确保生成的波形自动缩放为有意义的工程单位。生成的波形应缩放到的单位是原始波形单位除以时间(通常以秒为单位)。这种能力极大地简化了差异化操作。
其次,波形微分器不应要求数学协处理器来加快计算速度。这样的要求是惰性编程的副产品,只会给你的系统带来另一个成本负担。
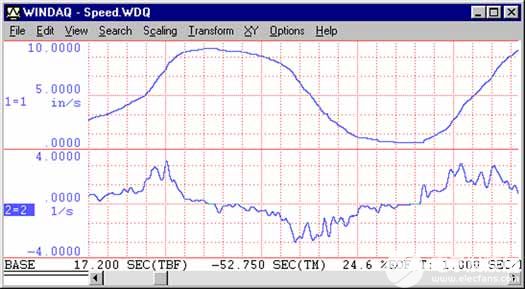
图 4—WinDaq回放屏幕的再现在顶部窗口中显示图 1 和图 3 的速度波形,在底部窗口中显示由高级 CODAS 计算的加速度波形。对导数函数应用平滑因子 15。
微分器应使用快速的整数数学运算,而协处理器则没有优势。唯一需要的浮点运算是计算缩放常数的单步,该常数将用于在需要时将微分波形缩放为有意义的单位。
最后,检查分析包的数据空间内存要求。一些分析软件实用程序要求要操作的波形完全驻留在半导体存储器中。如果要分析的波形长度仅为10Kb,则没有问题,但是在尝试处理2Mb或更大的通道时可能是一个真正的问题。为了使自己免受此类问题的影响,请寻找基于磁盘的分析包。此类系统将要分析的波形从磁盘上流出,通过微分器,并作为计算通道返回磁盘。使用这种方法可以分析的波形信息大小的唯一限制是硬盘驱动器的大小。
审核编辑:郭婷
-
深入了解 GaN 技术2023-12-06 7683
-
深入了解安全光栅2023-06-25 2188
-
带你深入了解示波器2022-02-07 975
-
深入了解主动电扫描阵列(AESA)雷达系统2021-05-24 3834
-
深入了解示波器|泰克内部资料2020-03-03 11610
-
深入了解电感与磁珠的异同2016-09-27 885
-
深入了解单片机汇编重要吗?2015-07-21 3338
-
深入了解LabVIEW FPGA资料分享2015-05-27 5210
-
单片机的深入了解!2014-10-12 3363
-
专家开讲:深入了解电池技术 ──Part 12014-08-18 4902
-
深入了解示波器2013-11-14 6142
-
深入了解示波器入门手册2013-03-27 1473
-
示波器的深入了解2009-11-04 730
全部0条评论

快来发表一下你的评论吧 !

