

卡诺图的降维操作讲解
描述
卡诺图的降维
从一道组合逻辑电路章节的课后题目入手:
[4-15]用中规模集成电路,设计一个路灯控制电路,要求能在四个不同的地方都可以独立的控制灯的亮灭。
【解析】
什么叫独立的控制灯的亮灭,如果是不管之前的状态是亮还是灭,其余每个开关都能使其状态发生改变(亮变灭或者灭变亮),这才叫独立控制,但是这样需要记住前一个时刻的状态,这就不是组合逻辑电路中的内容,而是时序逻辑电路。
所以此处独立是另外一种独立,即在其中三个开关状态相同,另一个开关状态不同的情况下可以控制灯的亮灭。
【题解】
首先列出真值表
设输入变量为A、B、C、D,输出变量为Y,则:

根据该真值表可得表达式:
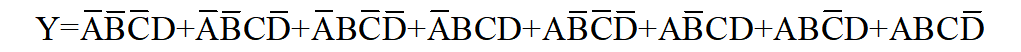
有表达式就好办了,接下来就是怎么实现该表达式,无非就是使用译码器、数据选择器等等。
[解法1]
直接一点,使用4-16译码器(当然,没有直接可以使用的4-16译码器,可先用2个3-8译码器进行级联)
上述表达式化成最小项的形式:
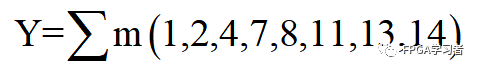
图略
[解法2]
再直接一点,使用16选1数据选择器。如图:
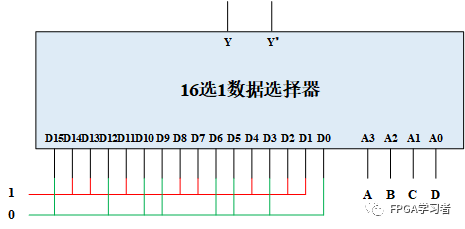
[解法3]
正常一点,使用8选1数据选择器:
使用8选1数据选择器,只有三个变量输入,那么就要想办法消除一个变量,这就到了本文的重点,使用卡诺图进行降维:
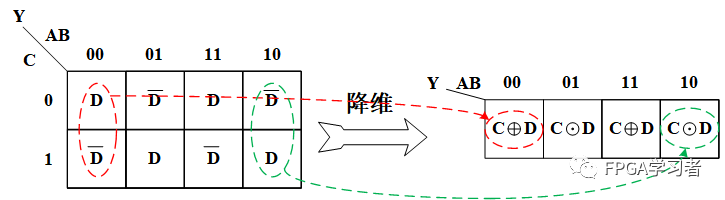
先画正常的四变量卡诺图,然后进行降维操作,比如此处消除D输入变量:
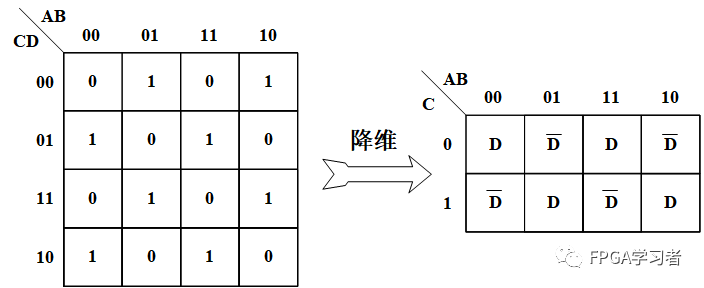
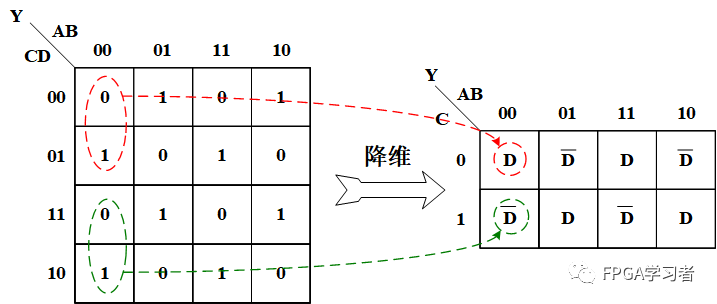
在图中,红圈圈的位置,当AB=00,C=0时,输出Y和D的值相同,所以降维后右侧红圈圈中填D。绿色圈圈同理,填入D非。
>====================<
[补充练习]
随便找一个卡诺图进行降维操作:
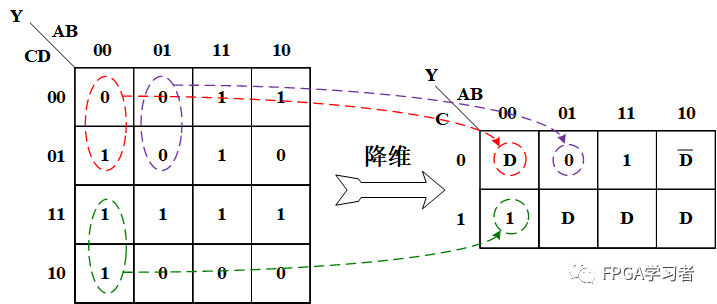
还可以再进行降维,这次消除B输入变量:
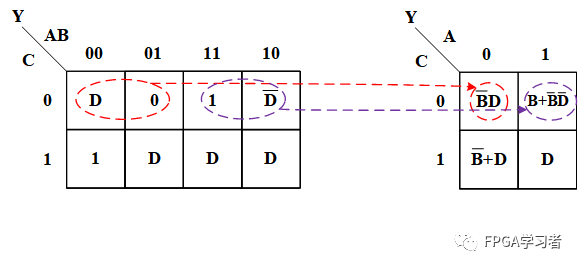
在第二个图红圈圈中,A=0,C=0的情况下,B=0时,Y=D,B=1是Y=0,所以降维后填B'D。其余几个格子同样操作。
其实降维,本质上就是一种折叠操作。
>====================<
再回到原来的题目上:
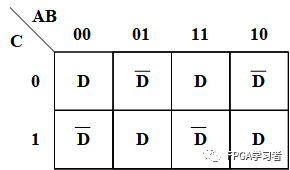
这样就是只有三个输入变量了,可以使用8选1数据选择器了,如下图所示:
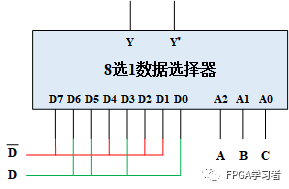
[解法4]
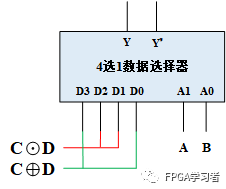
使用四选一数据选择器:
在上述卡诺图的基础上继续降维即可:
然后就可以使用四选一数据选择器了
审核编辑:郭婷
-
卡诺图如何化简2022-11-01 6566
-
数字逻辑基础卡诺图化简2019-05-30 3905
-
卡诺图化简法例题详解2018-03-07 331805
-
卡诺图简化方法及简化步骤介绍2018-03-01 60496
-
卡诺图小软件1.82016-12-17 1335
-
降维卡诺图在逻辑函数设计中的应用2012-04-18 2072
-
卡诺图,卡诺图是什么意思2010-03-08 13279
-
卡诺图的构成及其简法2010-02-27 12852
-
卡诺图化简法2008-09-27 2257
-
逻辑函数的卡诺图化简法2008-01-21 823
全部0条评论

快来发表一下你的评论吧 !

