Dijkstra和A*算法及其Matlab实现

写在前面的话：只是对两种路径优化算法进行简单的理解和尝试，为后续使用做准备。如果用到，请再次好好理解原理和Matlab源码。

首先给出Matlab下的三个脚本文件：

TestScript.m

 

%
% TestScript for Assignment 1
%


%% Define a small map
% map = false(10);
map = ans;
% Add an obstacle
% map (1:5, 6) = true;
map = logical(map);
start_coords = [1, 1];
dest_coords  = [40, 20];


%%
close all;
%   [route, numExpanded] = DijkstraGrid (map, start_coords, dest_coords);
% Uncomment following line to run Astar
  [route, numExpanded] = AStarGrid (map, start_coords, dest_coords);


%HINT: With default start and destination coordinates defined above, numExpanded for Dijkstras should be 76, numExpanded for Astar should be 23.

 

AStarGrid.m

 

function [route,numExpanded] = AStarGrid (input_map, start_coords, dest_coords)
% Run A* algorithm on a grid.
% Inputs : 
%   input_map : a logical array where the freespace cells are false or 0 and
%   the obstacles are true or 1
%   start_coords and dest_coords : Coordinates of the start and end cell
%   respectively, the first entry is the row and the second the column.
% Output :
%    route : An array containing the linear indices of the cells along the
%    shortest route from start to dest or an empty array if there is no
%    route. This is a single dimensional vector
%    numExpanded: Remember to also return the total number of nodes
%    expanded during your search. Do not count the goal node as an expanded node. 


% set up color map for display用一个map矩阵来表示每个点的状态
% 1 - white - clear cell
% 2 - black - obstacle
% 3 - red = visited 相当于CLOSED列表的作用
% 4 - blue  - on list 相当于OPEN列表的作用
% 5 - green - start
% 6 - yellow - destination


cmap = [1 1 1; ...
    0 0 0; ...
    1 0 0; ...
    0 0 1; ...
    0 1 0; ...
    1 1 0; ...
    0.5 0.5 0.5];


colormap(cmap);


% variable to control if the map is being visualized on every
% iteration
drawMapEveryTime = true;


[nrows, ncols] = size(input_map);


% map - a table that keeps track of the state of each grid cell用来上色的
map = zeros(nrows,ncols);


map(~input_map) = 1;   % Mark free cells
map(input_map)  = 2;   % Mark obstacle cells


% Generate linear indices of start and dest nodes将下标转换为线性的索引值
start_node = sub2ind(size(map), start_coords(1), start_coords(2));
dest_node  = sub2ind(size(map), dest_coords(1),  dest_coords(2));


map(start_node) = 5;
map(dest_node)  = 6;


% meshgrid will `replicate grid vectors' nrows and ncols to produce
% a full grid
% type `help meshgrid' in the Matlab command prompt for more information
parent = zeros(nrows,ncols);%用来记录每个节点的父节点


% 
[X, Y] = meshgrid (1:ncols, 1:nrows);


xd = dest_coords(1);
yd = dest_coords(2);


% Evaluate Heuristic function, H, for each grid cell
% Manhattan distance用曼哈顿距离作为启发式函数
H = abs(X - xd) + abs(Y - yd);
H = H';
% Initialize cost arrays
f = Inf(nrows,ncols);
g = Inf(nrows,ncols);


g(start_node) = 0;
f(start_node) = H(start_node);


% keep track of the number of nodes that are expanded
numExpanded = 0;


% Main Loop


while true
    
    % Draw current map
    map(start_node) = 5;
    map(dest_node) = 6;
    
    % make drawMapEveryTime = true if you want to see how the 
    % nodes are expanded on the grid. 
    if (drawMapEveryTime)
        image(1.5, 1.5, map);
        grid on;
        axis image;
        drawnow;
    end
    
    % Find the node with the minimum f value,其中的current是index值，需要转换
    [min_f, current] = min(f(:));
    
    if ((current == dest_node) || isinf(min_f))
        break;
    end;
    
    % Update input_map
    map(current) = 3;
    f(current) = Inf; % remove this node from further consideration
    numExpanded=numExpanded+1;
    % Compute row, column coordinates of current node
    [i, j] = ind2sub(size(f), current);
    
    % *********************************************************************
    % ALL YOUR CODE BETWEEN THESE LINES OF STARS
    % Visit all of the neighbors around the current node and update the
    % entries in the map, f, g and parent arrays
    %
    action=[-1 0; 1 0; 0 -1; 0 1];%上，下，左，右
    for a=1:4
        expand=[i,j]+action(a,:);
        expand1=expand(1,1);
        expand2=expand(1,2);
        %不超出边界，不穿越障碍，不在CLOSED列表里，也不是起点，则进行扩展
        if ( expand1>=1 && expand1<=nrows && expand2>=1 && expand2<=nrows && map(expand1,expand2)~=2 && map(expand1,expand2)~=3 && map(expand1,expand2)~=5)
            if ( g(expand1,expand2)> g(i,j)+1 )
                g(expand1,expand2)= g(i,j)+1;
                f(expand1,expand2)= g(expand1,expand2)+H(expand1,expand2);
                parent(expand1,expand2)=current;
                map(expand1,expand2)=4;
            end
        end
    end
    %*********************************************************************
    
    
end


%% Construct route from start to dest by following the parent links
if (isinf(f(dest_node)))
    route = [];
else
    route = [dest_node];
    
    while (parent(route(1)) ~= 0)
        route = [parent(route(1)), route];
    end


    % Snippet of code used to visualize the map and the path
    for k = 2:length(route) - 1        
        map(route(k)) = 7;
        pause(0.1);
        image(1.5, 1.5, map);
        grid on;
        axis image;
    end
end
end

 

DijkstraGrid.m

 

function [route,numExpanded] = DijkstraGrid (input_map, start_coords, dest_coords)
% Run Dijkstra's algorithm on a grid.
% Inputs : 
%   input_map : a logical array where the freespace cells are false or 0 and
%   the obstacles are true or 1
%   start_coords and dest_coords : Coordinates of the start and end cell
%   respectively, the first entry is the row and the second the column.
% Output :
%    route : An array containing the linear indices of the cells along the
%    shortest route from start to dest or an empty array if there is no
%    route. This is a single dimensional vector
%    numExpanded: Remember to also return the total number of nodes
%    expanded during your search. Do not count the goal node as an expanded node.




% set up color map for display
% 1 - white - clear cell
% 2 - black - obstacle
% 3 - red = visited
% 4 - blue  - on list
% 5 - green - start
% 6 - yellow - destination


cmap = [1 1 1; ...
        0 0 0; ...
        1 0 0; ...
        0 0 1; ...
        0 1 0; ...
        1 1 0; ...
  0.5 0.5 0.5];


colormap(cmap);


% variable to control if the map is being visualized on every
% iteration
drawMapEveryTime = true;


[nrows, ncols] = size(input_map);


% map - a table that keeps track of the state of each grid cell
map = zeros(nrows,ncols);


map(~input_map) = 1;   % Mark free cells
map(input_map)  = 2;   % Mark obstacle cells


% Generate linear indices of start and dest nodes
start_node = sub2ind(size(map), start_coords(1), start_coords(2));
dest_node  = sub2ind(size(map), dest_coords(1),  dest_coords(2));


map(start_node) = 5;
map(dest_node)  = 6;


% Initialize distance array
distanceFromStart = Inf(nrows,ncols);


% For each grid cell this array holds the index of its parent
parent = zeros(nrows,ncols);


distanceFromStart(start_node) = 0;


% keep track of number of nodes expanded 
numExpanded = 0;


% Main Loop
while true
    
    % Draw current map
    map(start_node) = 5;
    map(dest_node) = 6;
    
    % make drawMapEveryTime = true if you want to see how the 
    % nodes are expanded on the grid. 
    if (drawMapEveryTime)
        image(1.5, 1.5, map);
        grid on;
        axis image;
        drawnow;
    end
    
    % Find the node with the minimum distance
    [min_dist, current] = min(distanceFromStart(:));
    
    if ((current == dest_node) || isinf(min_dist))
        break;
    end;
    
    % Update map
    map(current) = 3;         % mark current node as visited
    numExpanded=numExpanded+1;
    % Compute row, column coordinates of current node
    [i, j] = ind2sub(size(distanceFromStart), current);
    
   % ********************************************************************* 
    % YOUR CODE BETWEEN THESE LINES OF STARS
    
    % Visit each neighbor of the current node and update the map, distances
    % and parent tables appropriately.
    action=[-1 0; 1 0; 0 -1; 0 1];%上，下，左，右
    for a=1:4
        expand=[i,j]+action(a,:);
        expand1=expand(1,1);
        expand2=expand(1,2);
        %不超出边界，不穿越障碍，不在CLOSED列表里，则进行扩展
        if ( expand1>=1 && expand1<=nrows && expand2>=1 && expand2<=ncols && map(expand1,expand2)~=2 && map(expand1,expand2)~=3 && map(expand1,expand2)~=5 )
%           if ( expand1>=1 && expand1<=nrows && expand2>=1 && expand2<=ncols && map(expand1,expand2)~=2 && map(expand1,expand2)~=3 && map(expand1,expand2)~=5)
            if ( distanceFromStart(expand1,expand2)> distanceFromStart(i,j)+1 )
                distanceFromStart(expand1,expand2)= distanceFromStart(i,j)+1;
                parent(expand1,expand2)=current;
                map(expand1,expand2)=4;
            end
        end
    end
    distanceFromStart(current) = Inf; % remove this node from further consideration
    %*********************************************************************


end


%% Construct route from start to dest by following the parent links
if (isinf(distanceFromStart(dest_node)))
    route = [];
else
    route = [dest_node];
    
    while (parent(route(1)) ~= 0)
        route = [parent(route(1)), route];
    end
    
        % Snippet of code used to visualize the map and the path
    for k = 2:length(route) - 1        
        map(route(k)) = 7;
        pause(0.1);
        image(1.5, 1.5, map);
        grid on;
        axis image;
    end
end
end

 

注：运行环境，Matlab 2019a 版本，安装 RTB（Robotic Tool Box） 工具包，链接地址为，RTB安装链接 。

该工具包中可以运行作者大佬写到的matlab/simulink四轴历程，只需要使用指令 sl_quadrotor 即可。

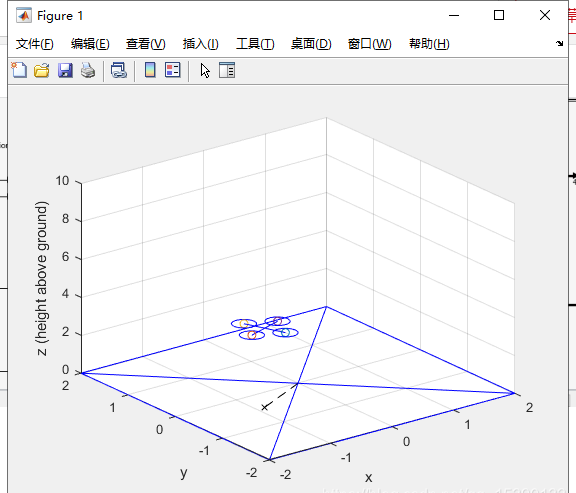
使用方法

在Matlab 中，使用 makemap(30) 来生成地图，通过鼠标来设置障碍形状。该例子生成了一个30*30的方阵，然后直接运行TestScript.m即可。

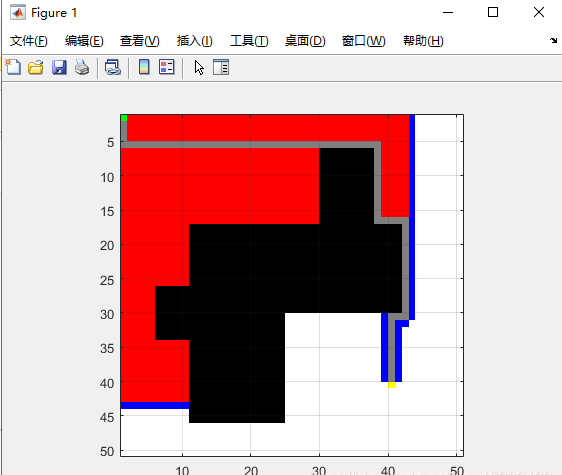
其中要在TestScript.m中选择是采用A算法，还是Dijkstra算法。同时设置起始点和终点在哪。下图显示得到的A算法路径优化结果。

其中绿色点为起点，黄色点为终点，黑色表示障碍，白色表示空闲，红色表示搜寻过，灰色表示最后规划的路径。

下图显示Dijkstra算法的路径优化结果：

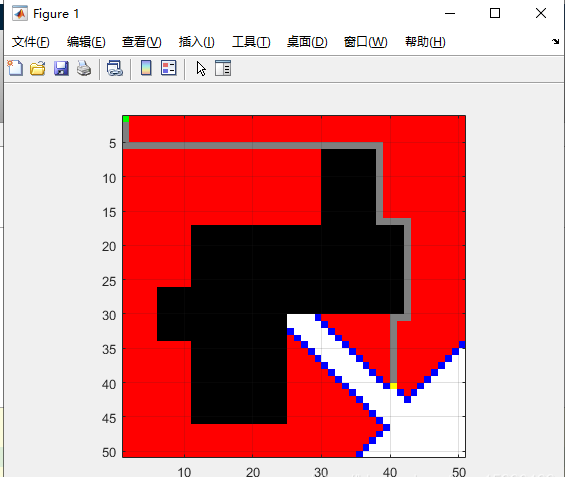
对应的动态效果已经录屏，下面给出传送门（录屏水印广告请忽略）：

通过对比可以看出：A* 算法搜索速度较快，毕竟里面有贪心算法。

这在地图较大的场景应用较好。但是A*算法只能得到局部最优解，并不能保证全局最优解。

相比之下，Dijkstra算法尽管搜索速度慢，但是是全局最优解。不知道两种方法结合gmapping，hector或者cartographer生成的栅格地图会是什么样的效果。后面期待尝试一下。

　　审核编辑：汤梓红