滤波器设计中的椭圆函数

是翻译自IEEE上关于滤波器设计中所用到的椭圆函数知识，文章非常经典，值得拜读。限于译者水平，文中有不少翻译不恰当的地方，希望读者提出宝贵意见，批评指正。英文原文见附录 。

 

 

摘要

本文简要介绍了雅可比椭圆函数(Jacobian elliptic functions)和兰登变换(Landen transformation)的基本性质，将它们与三角函数和双曲函数联系起来，从而提供了一个评估椭圆函数的最准确方法。解释了椭圆函数在创建等波纹低通滤波器中的应用，并通过示例说明了它们的数值计算方法。包括一个用于设计的Fortran程序，并给出了一个更快、更准确的替代Matlab的ellipap函数的方案。

I. 引言

自1930年代以来，人们就知道在通带和阻带中具有等纹波响应的低通滤波器的传递函数可以用雅可比椭圆函数(Jacobian elliptic function)来精确描述[1]。这种滤波器也被称作卡尔滤波器(Cauer filter)、椭圆函数滤波器(elliptic-function filter)，有时干脆被称为椭圆滤波器(elliptic filter)，最后一个名字不推荐使用，因为它暗示滤波器是蛋形的！它们过去被广泛用于各种模拟滤波器，现在也经常应用于IIR数字滤波器中。

遗憾的是，很少有工程师在他们的教育过程中接受过任何关于椭圆函数性质的相关课程，并且人们认为他们的数值计算(如滤波器设计的那样)既复杂又困难。这也促使了几位作者设计出无需使用椭圆函数的设计此类滤波器的方法[2]-[5]。达林顿(Darlington)在文献[6]、[7]中提供了一种巧妙的方法是将切比雪夫有理分数改为一系列的变换，最终得到了奇数阶椭圆函数滤波器的传递函数。

本文章的目的是简单描述雅可比椭圆函数的性质，以及它们在应用于滤波器问题时与三角函数和双曲函数的关系。在这里并没有试图给出该理论在数学上严格和形式化的结果，或者证明；目的只是传达对这些函数的一般特性的理解。假定读者接受了典型的工程本科教育，其中包括复变理论的课程。强烈推荐有兴趣想要更详细地研究该主题的读者阅读Neville 的经典著作[8]，必须承认这是一本不太适合随便参考的书。

对雅可比椭圆函数的讨论引出了对兰登变换的描述，从而引出了非常准确的计算这些函数的方法。在此背景下，我们展示了如何使用椭圆函数通过一对参数方程的方式来定义所需的滤波器响应，其与使用三角函数来定义切比雪夫滤波器的方式完全相同。最后，我们讨论了如何通过兰登变换计算传递函数零极点的细节。该论文包括一个用于执行设计的Fortran程序和一个数值示例来说明这些步骤。本文还给出了一个更快、更准确的替代Matlab的ellipap函数的方法。

II. 周期函数

A. 单周期函数

在复数域下的所有函数中，椭圆函数的特点是其双周期性质。在这方面，它们类似于非常常见的单周期初等函数，但比它们复杂一些。具有周期为  的单周期函数  对于所有  满足关系  ，对于所有整数  也满足  。

基本初等函数  是单周期的，具有虚周期  ，并且这个虚周期由双曲函数  和  共享，原因是它们只是  与  的线性组合。将指数函数中的  替换为  会将其转换为具有实周期  的单周期函数，它由三角函数  和  共享。

单周期函数变量的复平面根据周期性可以看作被分解为无限个宽度为  且等于周期值的全等周期带。对位于这些条带中的任意点  ，在每个其他条带中都会有一个全等点 ，这样所有这些点的函数值都是相同的。  和  的周期带宽度为  并且无限长，并排平行于虚轴，而  和  的周期带形状与之相同，只是它们平行于实轴，如图1所示。

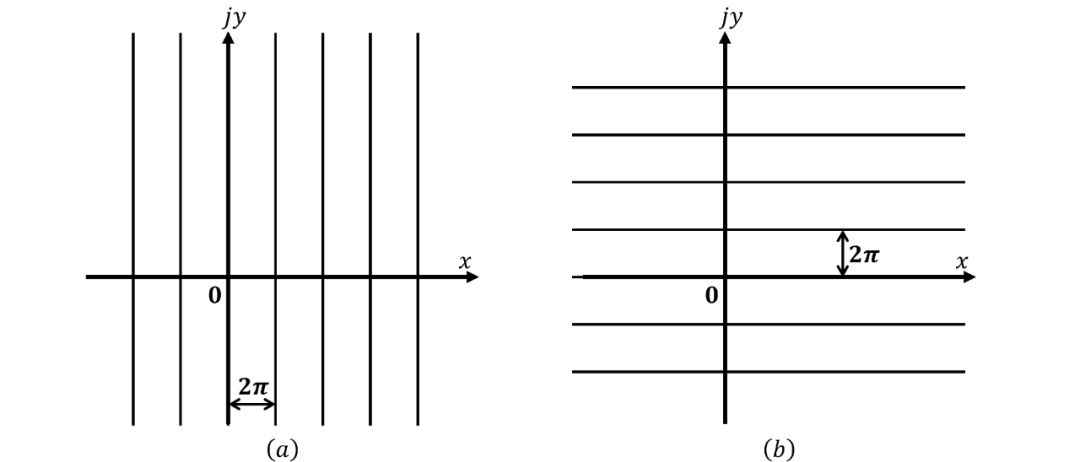
图1 (a)   和(b)   的周期带

相比之下，函数  和  的周期分别为  和  ，因此它们的周期带的宽度为  ，而不是  。如果  ，其中  是三角或双曲正弦或余弦，我们会发现一条宽度为  的无限带，以函数的零点为中心，即，周期带的一半，将一一映射到整个-平面上，而如果  是正切函数，则  是整个周期带映射到整个-平面。

B. 双周期函数(椭圆函数)

单周期函数的存在引出了一个问题，即，是否存在具有两个或更多个不同周期的函数？不难证明：1)一个函数不能有三个或更多个周期，2)如果一个函数有两个周期，周期的比不可能是实数；换句话说，周期必须指向复平面中的不同方向，而不是沿着同一条直线上。仅受此限制，我们可以构造一个单值双周期函数，其中两个周期分别是复数  和  ，因此对于所有  和所有整数  和  有  。

双周期让-平面上的所有  所构成的无限二维点阵相互关联。在这些点周围可以看到无限个周期平行四边形阵列，每个平行四边形的边分别为  和  ，这样，对于任何  值，网格在平行四边形中会形成一组全等点。由于点阵  可以同样很好地被  或  描述，可以取如  ,  和  中的任意两个，很明显，周期不是很具代表性，这将改变相应周期平行四边形的形状，但不会改变面积。

在每个周期内，平行四边形  必须至少具有一个奇点，要么就什么都没有，因此根据刘维尔定理(Liouville’s theorem)它将是一个常数。此外，在周期平行四边形边界周围的积分必须为零，因为由于周期性，平行四边形对边对积分的贡献将抵消。因此，根据柯西留数定理(Cauchy residue theorem)，平行四边形内奇点处的留数之和也必须为零。由于具有零留数的简单极点根本就不是极点，因此最简单的椭圆函数要么有一个具有零留数的双极点，要么有两个具有相等且相反的留数的简单极点。

椭圆函数的复杂性或阶数（order）由包含在周期平行四边形内的极点阶数之和来衡量。我们看到没有一阶的椭圆函数，以及两种不同的二阶椭圆函数。很容易理解，如果  是一个椭圆函数，那么  也是，且具有相同的阶数和周期。由此可知，二阶椭圆函数在每个周期平行四边形中具有一个双零点或两个单零点。

魏尔斯特拉斯(Weierstrass)首先描述了一个二阶椭圆函数，每个平行四边形有一个零留数的双极点，并以他的名字命名。它的简单性使其成为该学科理论的基本工具，也可以用作系统构造每个平行四边形有两个简单极点的二阶椭圆函数的"垫脚石"，魏尔斯特拉斯函数适当归一化后就变为我们所关注的雅可比函数。对于实际应用，雅可比函数比魏尔斯特拉斯函数更有用，而且雅可比函数的发现要早了几十年，它们每个平行四边形也有两个简单的零点以及两个简单的极点。

III. 雅可比函数

就像有六种不同的三角函数一样，即正弦、余弦、正切和它们的倒数，雅可比椭圆函数有十二种。正如正弦和正切的周期分别为  和  ，所以雅可比函数也有一组周期与另一组之间相差两倍的周期，长期以来，标准的做法是用被称为四分之一周期的量来描述周期，它对椭圆函数的作用与  对三角函数和双曲函数所起的作用相同。

雅可比函数应用到的实际问题的性质通常要求一个四分之一周期是实数(用  表示)，而另一个四分之一周期是虚数(用  表示)，我们将把讨论限制在这个特殊但非常重要的实例上。变量复平面第一象限的四个角分别在  、  、  和  的矩形称为基本矩形(the fundamental rectangle)。这个矩形的四个角分别用字母表示，原点(起点, Start，译注，也可以用相位为0的sin助记)的角是S，对角(Diagonally)的角是D，重合(Coincides，译注，也可以用相位为的cos助记)于实轴的角是C，垂直(Normal)于实轴的角是N(本描述中的头韵用作助记符！)，具体排列如图2所示。

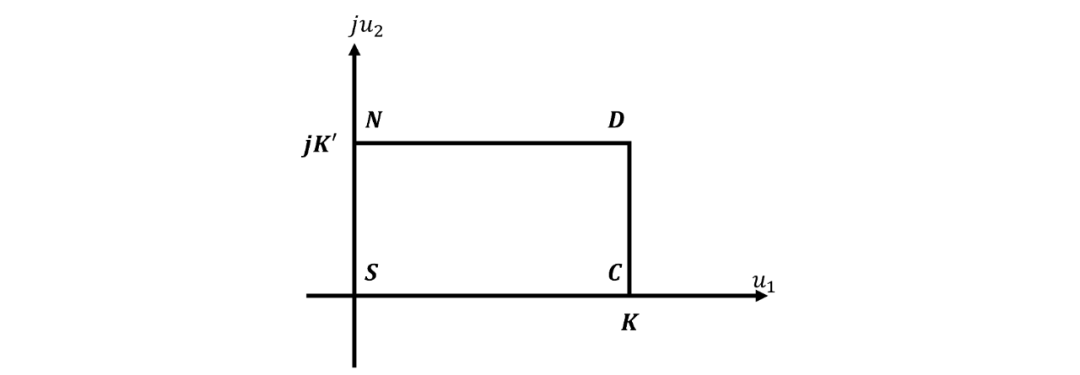
图2 基本矩形

每个雅可比函数在这个矩形的一个角处都有一个零点，在另一个角处有一个极点。由于零点可以先放置在4个角中的任何一个，然后将极点放置在其余3个角中的任何一个，所以总共有  种可能性；这就是上面所提到的12种不同的雅可比函数。每个函数都有一个由两个字母构成的名称，其巧妙地表明了他们的零极点组合模式，第一个字母表示包含零点的角，第二个字母表示包含极点的角。因此，如  函数表示在S处具有零，在N处具有极点，以此类推。

然后，12个函数中的每一个的零极点模式都相当简单地从基本矩形延伸到复平面的其余部分。每个函数的极点和零点都排列在相同的基本格点上，即所有整数  和  的  ，并且仅通过格点距原点的位移  来彼此区分。该位移等于基本矩形角处特定函数的极点或零点的位移。例如，  函数的极点在N，  ，因此极点集合在  ，而零点在S，其中  ，所以零集合位于  。三个典型函数  、  、  的零极点模式如图3所示。

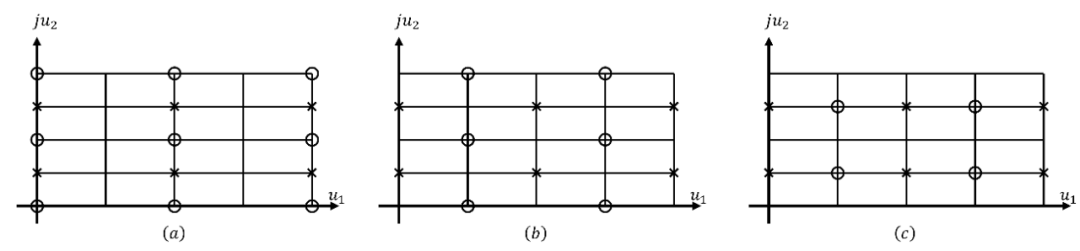
图3 a)   , b)   , c)   的零极点模式

当然，在基本矩形的边界周围，从零点到每个雅可比函数的极点有两条可能的路径。一条包含矩形的边位于正实轴上的路径，函数将其映射到整个正实轴上，而另一条路径将被映射到整个正或负虚轴上。基本矩形边界上的函数值总是在有极点或零点的角处由实数变为虚数，反之亦然。这意味着每个雅可比函数都将基本矩形映射到第一象限或第四象限。

如果我们将变量  的整个平面可视化为由与椭圆函数  的基本矩形一致的矩形所覆盖，并且矩形的角在  处，如图3所示，然后每个这样的矩形将被  映射到-平面的四个象限之一。其中四个矩形的任何其中心处函数  值为零的  块将始终映射到整个  -平面上。例如，  函数在原点有一个零，围绕这个零的四个矩形将映射到整个-平面上，如图4所示。

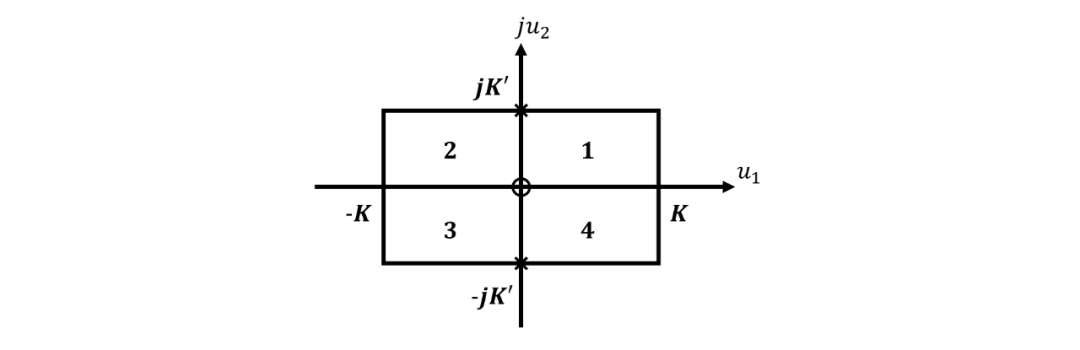
图4 对于  ， -平面中显示的四个矩形映射到整个 -平面上，每个矩形中的数字是其映射到的  -平面中象限数字

如果需要，可以将三角函数的周期指定为函数的独立参数，但对于定义和制表来说，将周期固定为  或  并让用户调整变量的比例来确定周期会更简单。同理，雅可比函数可以将它们的实部和虚部四分之一周期作为两个独立的参数。但是函数的基本属性只取决于基本矩形的形状，而不是其绝对大小，标准做法是用一个参数来指定这个形状，让大小自动调整以满足某些规范化的约束。

雅可比椭圆函数起源于计算椭圆弧长时使用的积分求逆，并由此衍生出它们的名称含有椭圆二字。例如，函数  完全由如下积分定义 在这个积分中出现的参数  被称为模数(不要与表示复数大小的模长相混淆)，对于我们正在考虑的实际情况，它是满足  的实数。它通常通过模角  确定为  。与  相关的另外一个量是补模  。通常，一个正在待求的函数的模是已知的，并且不需要在每个函数出现时明确说明它，但如果必须明确，我们会写成  。

这种定义雅可比函数的方式不仅会使四分之一周期  的比率固定为单个参数，而且它们的绝对大小也固定，从而实现了所有十二个函数非常简单的归一化。特别是，在原点处具有零或极点的六个函数(  、  、  、  、  、  )是奇函数，如果为零点则导数为1，如果极点则留数为1. 其余六个函数(  、  、  、  、  、  )是偶函数，并且在原点处为1。这种归一化的另一个结果是，如果  表示  ,   ,   ,   中的任意三个，则雅可比函数满足公式  。  、  、  这三个函数是雅可比在1827年通过反转椭圆积分获得的原始函数，其他九个函数是1882年由Glaisher引入的，作为前三个函数的倒数和商。

如果在(1)中，我们令  并注意到  ，我们得到四分之一周期  的一个以模数  的积分表达式，即 如果在(2)中将  替换为  ，则所得积分给出  而不是  。当  时，(1)中的积分简化为  函数的积分，我们得到  。由  ，我们从(2)中看到当  时  。类似地，当  时，(1)中的积分简化为  函数的积分，我们得到  。在这种情况下，当  时，(1)中的积分发散，因此从(2)我们看到当  时  。通过在(2)中将  替换为  ，我们可以推导出当  (并且  )和  时  当  (并且  )。

三角函数和双曲正弦和余弦的平方满足简单的线性关系，即 从这些可以找到所有剩余的其他三角函数和双曲函数。雅可比函数具有与这些完全相似的性质。它们位于共极点的三个函数  、  、  中的任意两个之间。三个经典函数形成这样一个极点在  的集合，并且满足 使用上面给出的性质，可以推导出其他三组共极点函数之间的关系。

最后，我们考虑将雅可比函数的参数从更改为的效果，有时称为雅可比虚变换。这种变换相当于将-平面绕原点旋转  ，当应用于三角函数或双曲函数时，会将一类函数的周期带旋转到另一类函数的周期带中。例如，我们得到如下众所周知的结果 对于雅可比函数的基本矩形，这个围绕原点的  旋转等同于平面围绕通过原点的  线的旋转。然后很明显，在基本矩形中，实数和虚数的四分之一周期  和  相互交换，对于  和  也是如此。除了位置互换外，四分之一周期的大小并没有变化。

基本矩形的这种旋转在其两个角处带有极点和零点。因此，在旋转后标记为S或D的拐角处的极点或零点仍将位于这些相同的标记拐角处，但标记为C的拐角处的极点或零点将出现在标记为N的拐角处，反之亦然。因此，在任何如此变换的雅可比函数的名称中，我们必须将  更改为  并将  更改为  ，然后将模数从  更改为  。对于三个经典函数，我们得到以下结果： 其余九个函数的结果可以通过这三个函数的商和倒数得到。六个奇函数将包含因子  ，与  函数一样，而六个偶函数将还是保持实数值，与  和  函数一样。

尽管我们一开始注意到双周期是所有椭圆函数的显著特征，但详细了解十二个雅可比函数中的每一个都具有哪些周期对我们目前所讨论的内容用处不大，读者可能已经推断出，我们稍后将继续深入讨论周期是  和  的  和  函数。

IV. 兰登变换

如果模数  趋于零，则比率  将趋于无穷大，雅可比函数及其周期矩形将分别退化为三角函数及其周期带。相反，如果  趋于1，  将趋于零，雅可比函数及其周期矩形将退化为双曲函数及其周期带。在三角函数极限  ,   ,   和  ，而在双曲函数极限  ,   ，  ，  。带撇号参数和不带撇号参数之间完全对称。

这表明椭圆函数占据了从一端的三角函数到另一端的双曲函数的连续路径，  和  作为沿其位置的对称度量。在路径的中心，基本矩形是一个正方形，  和  。兰登变换是一种通过修改  或  以使每一步中的  比率加倍或减半，并沿此路径在任一方向上以离散步骤移动的方法。这种变换前后的函数值的变化在代数上可以非常简单地实现。

四或五次连续变换通常足以满足设计要求，这样在滤波器设计中出现的任何实际值  移动到椭圆函数在数值上达到与极限的三角函数或双曲函数无法区分的点。三角函数或双曲函数是可以被计算出来的，然后通过计算中间椭圆函数，并通过连接它们的代数关系，最终找到所需的椭圆函数。在滤波器设计中，即使从双曲函数端可能需要稍微少一些变换步骤，但从三角函数端执行这个计算会更简单，这是因为开始计算所需的三角函数比双曲函数更容易找到。考虑函数 其中，我们将  作为变量  上的比例因子，以便使基本矩形沿-平面中实轴的边归一化而与  值无关。公式第一项在  处有极点，而第二项在分母中的  函数的零点  处有极点。所有这些极点上关于变量  的留数值为  。第二项分子中的因子  是必需的，因为分母中  函数零点对  具有  的导数。因此，整个函数在  处有极点，留数为  。这些正是其模数被选择为使其四分之一周期比率  的一半的  函数的极点。

给出函数  ，其中选择模数  使得四分之一周期  和  满足  。使用这个结果，我们看到  的极点位于  。当  时，  和  都等于1，因此需要一个因子  来满足以下恒等式： 具有模数  的  函数是比具有模数  的  函数更远离三角函数末端路径的一个兰登变换，并且(8)是上面提到的代数关系。由四分之一周期因子对  实现的归一化以及由变换引起的形状变化导致模数  的基本矩形恰好占据模数  矩形的下半部分。

与(8)相同的结果也适用于函数。和函数的极点和零点都沿着平行于虚轴的线交错排列，即平行于三角函数的周期带，这使得它们适合从三角函数端跟踪路径。接下来，为了补充(8)中的关系，我们需要知道如何从  计算  。

这可以通过在以模数  的基本矩形的D角处来评估公式(8)两侧的等式，即在点  处。从上面的注解可以看出，模数  矩形的D角仅是模数  矩形中从C角到D角的边的一半。  函数在其D角处的值等于其模数，而从C到D中间的值等于模数的平方根。使用这些信息，我们发现(8)在这个  值下减少到  。

为了以更适合以计算的形式来组织符号，我们用  和  分别表示椭圆函数的模数和四分之一周期，这些椭圆函数是  个连续向三角函数端的兰登变换，其中  是一个整数，  对应于所求函数。在这种表示法中，上面的结果变为 将(9)求逆得到关于  的一个二次方程，其两个根互为倒数。因为  要小于1，我们必须在这里选择较小的那个值，它可以写成数值计算稳定的形式 (10)中的递推生成一个模数序列，随着  的增加迅速趋于零，当模数小于  时终止，其中  是小数位数。请注意，模数大小的减小不是通过减法来实现的，而是通过除法和平方来实现的，这可能会对数值精度产生除了通常的舍入影响外的不利影响，整个序列将保持完整的  位数字精度。

虽然只有十二个雅可比函数中的两个，即  和  ，可以从三角函数端回溯，其他十一个函数中的任何一个都可以通过使用从(4)导出的关系从而可以从这两个中的任何一个求解。幸运的是，滤波器问题主要使用  或  ，它们只需要依据对应函数的倒数来求解。另外  函数是  函数移动了四分之一周期，即  。在新表示法中，  和  函数都满足(8)的重写版本，即 与(8)中一样，所有椭圆函数的参数都表示为适当四分之一周期的某个分数，这里用a表示。这对于滤波器应用来说特别方便，因为几乎所有需要的椭圆函数都有这样的参数自然地显示为四分之一周期的固定分数。因此当路径接近三角函数的末端时，这个参数的极限值是  ，式(11)中的  递归从  开始。  的与之类似的过程将从  开始。

如果我们将椭圆函数转换为路径末端是双曲函数，那么用于跟踪椭圆函数的是  ，而不是  。我们再次将整数下标  附加到模数和四分之一周期以指示在向双曲函数末端进行  次兰登变换后获得的值。不应与前面描述的下标混淆，因为我们不会同时使用两条路径。

与从三角函数端开始的路径一样，从双曲函数端只能寻得两个雅可比函数。这些是  和  函数，它们的极点和零点沿着平行于实轴的线交错排列，即平行于双曲函数的周期带。  或  公式的推导，对应于(8)，几乎遵循相同的套路，但有一点不同，现在，用于模数  的  -平面中的基本矩形必须占据用于模数  的矩形的左半部分(而不是下半部分)。这需要选择  ，使得  ，并在左侧的变量  上用一个因子  代替  。与  的相邻值相关的公式与(10)中的  相同，并且是 这与增加  的方式与前述完全相同，就像(10)中的  一样，序列以相同的方式终止。

与  函数的(11)对应的是  函数的递归方式   函数的递归与之前唯一不同点只是在方括号内的两主项之间的符号。

在三角函数的末端  具有极限值  ，因此起始三角函数具有简单的参数  。但是，在双曲函数的末端，  趋于无穷大，只有  具有唯一的极限值。因此，起始双曲函数的参数是  乘以这个极限值。如果我们采用  次变换来达到与双曲函数的数值相等，我们必须首先使用例如以下近似值来计算  ，该近似值源自  函数[8]的理论，当  非常小时，有 然后，(13)中  递归的起始双曲函数是 我们通过展示寻找  函数值的步骤来说明这些计算方法，首先从三角函数端开始，然后从双曲函数端开始。整个过程都使用了相当于14位小数的双精度计算。表I显示了从三角函数端计算所涉及的量。为了简化显示，只给出了所用14位数字中的前十位。五次变换足以将模数减小到小于  ，并且在表中与这个最小模数相邻的是  ，它是起始的三角函数。在通过(11)跟踪到  之后，我们得到相应的  函数值。其倒数是  。

表II显示了从双曲函数端的类似计算。这里还需要五次递归来将补模降低到  以下。在这个阶段，我们使用(14)找到实际四分之一周期  然后除以  得到  。其值的三分之一作为  函数的参数代入，得到的值放入  与最小的补模相邻的位置上。然后使用(13)将  函数递归到  ，并通过(4)找到想要的  函数，重新写作为  . 这给出了与之前从三角函数端计算的函数相同的值，到14位小数精度。

V. 椭圆函数滤波器

在电子滤波器发明之后的前半个世纪里，设计师使用了一种似乎是描述其行为的最自然的方式，即输入/输出传递函数。但是，随着使用输出/输入传递函数的系统理论的发展，滤波器设计者被说服(委婉地说)采用相同的惯例，例如，我们现在将纯无源滤波器的响应绘制为增益，以分贝(dB)为单位，所有纵坐标均为负值！我们无意在此争论这两种选择的优点，而只是指出在本文中我们使用输入/输出传递函数  来描述行为(译注，本文使用了传统的插入损耗，全部是正值，和我们平常看到的滤波器频响曲线上下颠倒)。

我们希望讨论的低通滤波器，在通带中损耗具有等纹波响应，在阻带中具有等最小值响应，这可以看作是通带中的损耗是等纹波并且在阻带中单调递增的切比雪夫滤波器的推广。为了使前者的描述更容易理解，我们先分析切比雪夫滤波器，然后由简入繁的逐步推广到椭圆函数滤波器。

我们由三个复变量  、  和  所构成的参数方程来定义归一化的切比雪夫滤波器 其中 是峰峰值幅度的等纹波通带损耗且  。当然，可以联立(16a)和(16b)消掉参数  并最终得到一个包含切比雪夫多项式的方程，但以这种形式进行分析更加困难。在这里使用  代替单个参数变量  ，以便能够在稍后作为雅可比四分之一周期出现因子  。整数  定义为多项式  的阶数，并满足(16a)中余弦的周期带宽度是(16b)中余弦周期带宽度的  ，因此前者周期带的  倍恰好和后者并排重合。

为了找到滤波器的自然频率，即  的零点，我们令(16a)为零并求解以获得  的相应值。然后将这些代入(16b)以获得  和  的所需值，令(16a)为零，得到 要使  成为复数，那么必须是位于-平面中映射到余弦平面的虚轴上的那些线上。这些是平行于-平面中虚轴的线，实轴值为  。因此，如果  ，有 或 对于这些  的值 因此从(18)我们可以让 对右侧取负值会使  有与(21)完全相同的一组零点。从这些我们必须提取位于-平面左半部分的那些以获得  的零点，对于求解(21)给出 令 我们得到自然频率的表达式为 由于  是一个多项式，它在  处有一个  阶极点。

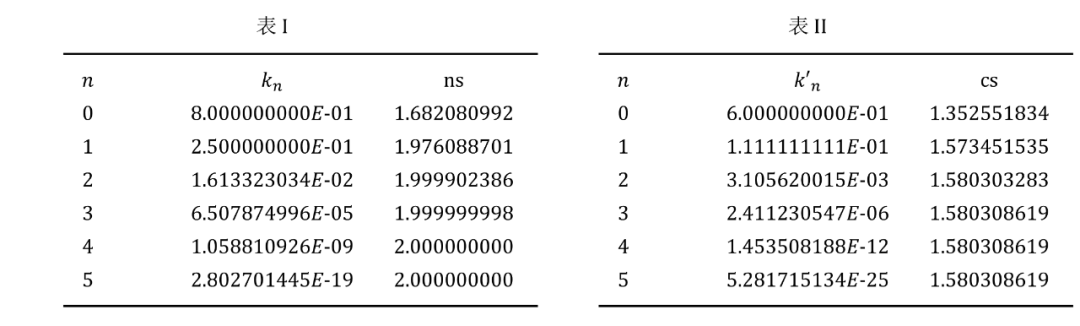
要将切比雪夫滤波器推广到椭圆函数滤波器，只需将(16)中出现的余弦函数更改为与它们等价的椭圆函数。但是我们发现有两个不同的椭圆函数  和  ，当  时，它们的极限都是退化为同一余弦函数，让我们的应用变得清晰的唯一正确选择是考虑通过式(16b)映射到正实  轴的-平面的路径。实轴  映射到通带  ，而虚轴  映射到阻带  。-平面中的原点是将等波纹通带与单调递增阻带分隔点(译注，即所谓的3dB截止频率点)。切比雪夫滤波器本身没有明确的过渡带，与阻带不同，尽管它必须满足的指标中通常包括有一个。

另一方面，椭圆函数滤波器在等波纹通带和等最小阻带之间确实有一个显式过渡带，这需要在-平面上映射到具有对应于通带、过渡带和阻带的三个不同段的正实轴  上，只有函数可以做到这一点。围绕基本矩形的路径，从C处的零点到D处的极点，映射到  函数的正实轴，穿过矩形的三个边，然后可以将它们设置为对应于三个所需的带。

我们首先定义滤波器方程，然后再解释它们之间的关系，他们是 其中  和  是与(25b)中的与模数  相关的四分之一周期，而  和  类似与(25a)中的模数  相关。如前所述，整数  定义为有理函数  的阶数(degree)，通带纹波由(17)给出。

(25b)的-平面中基本矩形的边界到-轴的映射如图5(a)所示，它表示  值与矩阵角的关系，角的三条边分别对应于通带、过渡带和阻带。对于切比雪夫滤波器和椭圆函数滤波器，由于在变量  中包含了四分之一因子  或  ，归一化的通带  映射到相同的范围  。阻带的边缘在  ，这定义了模数  。

另一个椭圆函数的模  是通过满足(25c)中所规定的四分之一周期条件的需要而隐式选择的。这种情况导致  的基本矩形的形状和大小(在变量  中)必须满足  个这样的矩形可以精确地并排重合于  。图5(b)显示了对于  的情况，  的零极点模式和函数值如何叠加在  的基本矩形上。

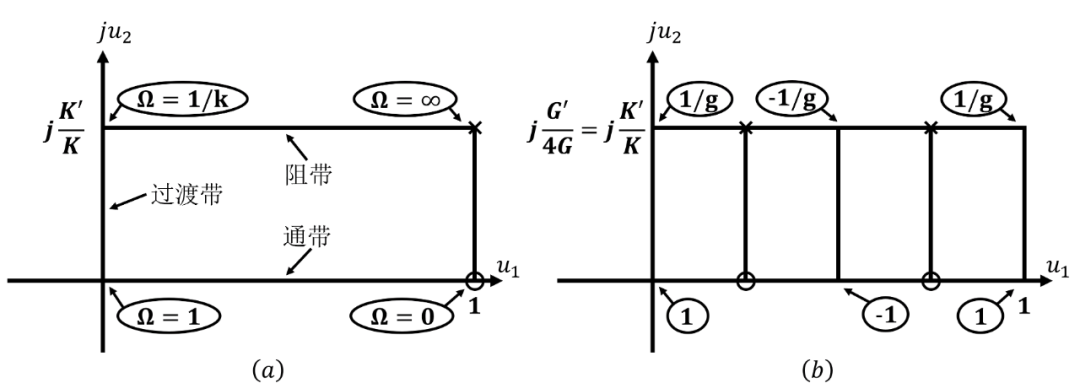
图5 在  条件下, (a)    和 (b)   在-平面上的映射

正是通过选择  来满足(25c)，以及由此产生的两个基本矩形的简单几何关系，使得  成为  的有理函数，正如  是  中的多项式一样。请注意，当  趋于零时，  也趋于零，然后(25a)和(25b)分别退化为(16a)和(16b)。这将使椭圆函数滤波器在极限条件下转化为切比雪夫滤波器。事实上，椭圆函数滤波器的过渡带，而不是它的阻带，在这个极限下变成了切比雪夫滤波器的阻带。

要找到的自然频率，我们使用与切比雪夫滤波器相同的方法，令(25a)为零，得到 为了使  是虚数，  必须位于-平面中映射到函数为虚轴的那些线上。这些是平行于-平面中虚轴的线，它们穿过  的极点和零点，并且在实轴上的值为  ，因此 或 这正是切比雪夫滤波器在(19)中所找到的值。可使用(6)直接推广(20)，得到 所以由(26)我们可以取 这和式(21)对应。

下面我们通过一系列兰登变换将(25)中的椭圆函数及其参数变换到兰登链的三角函数末端。我们首先使用(10)生成模量  的降序序列，并在椭圆函数与三角函数在数值上无法区分时以  终止。然后我们创建对应的序列  。然而，我们没有显示地给出  ，只有它与(25c)隐含的与  的关系。当后者在  次兰登变换后可以看到，  和  将在  处相等，因此(25c)简化为 正如我们可以使用(14)在双曲函数端从  计算  ，所以当  非常小时我们可以使用(14)的补从三角函数端的  中找到  。在一些简单初等代数计算后后，得到 根据  的这个值，我们可以使用递归式(9)将序列  后向构造到  ，得到 对于较大的  值，(31) 可能会生成一个小于浮点运算下限(非零)的  ，因此无法通过(32)计算  的兰登链。如果发生这种情况，可以从  计算  ，甚至可能是  。这为  提供了比  更短的兰登链，并反映了与  相比减小了  的大小。在这些非常小的  值下，可以安全地用统一替换为  ，然后(32)简化为  ，将其代入(31)得到 和 一旦我们有了  ，我们可以使用(25a)中  函数在阻带损耗最小处的值等于  的事实，通过公式求得损耗为 计算出模数  和  的两个序列后，剩下的任务就是找到  的零点和极点。我们首先考虑复零点的稍微复杂的情况。兰登变换被描述为通过(11)中的递归从实数极限三角函数值中获得实数椭圆函数的值。但这些都是解析函数，因此递归也适用于这些函数的复数也就不足为奇了。我们只需要为正确的切比雪夫滤波器找到  的复数值，如(24)所示，并通过(11)将  函数的倒数从模数  转换回模数  。这些变换的最终结果的倒数便给出了想要的自然频率。

切比雪夫滤波器由两个参数定义，阶数  和控制通带波纹大小的量  。显然，正确的切比雪夫滤波器的阶数将与所需椭圆滤波器的阶数相同，但两个滤波器的通带纹波幅度表明彼此之间略有不同。原因在于(29)，它表明椭圆函数滤波器的  值本身等于一个椭圆函数，当系统转换为三角函数链的末端。我们必须考虑在这个过程中如何修改  的给定值。

我们首先写出(29)的倒数，并在  的给定值上附加一个下标零，以准备生成一系列值，就像我们对  和  所做的那样： 在完整的兰登变换链中，模为  的椭圆函数在  处归结为三角函数，在  处归结为双曲函数。但是对于模为  的椭圆函数，情况正好相反；当  时，它们将简化为双曲函数，因为那时  。因此，当我们将(25)的主要椭圆函数转换为末端为三角函数兰登链时，我们必须意识到出现在(35)中的  函数，其模为  ，实际上将是双曲函数的终点。

从双曲函数端跟踪  函数的递归在(13)中给出，但不同的是这里的模是  ，而不是  ，所以这两个量所起的作用是互换的。因此，从  到  跟踪它的  (代替它所代表的椭圆函数  )的递归将是 但是我们从  开始，想要  ，而不是相反，所以我们必须求(36)的逆，得到 其中 在大多数情况下，从  到  的值变化非常小，并且(37)中的递归经常被省略。切比雪夫滤波器中的通带纹波大小简单地等于椭圆函数滤波器的指标值，然后最终得到的纹波大小比设计的要小一些。纹波的精确幅度通常不是很关键。

下一步是使用(24)找到切比雪夫滤波器的自然频率，  的值从(37)中找到。  函数在(11)中的递归涉及  倒数的值，如(25b)中所定义，并且必须修改为  倒数的递归。这只需要改变最后一项的符号。因此，如果是典型复自然频率的倒数，从  作为切比雪夫滤波器的倒数，我们得到递归   的倒数是椭圆函数滤波器  的相应自然频率或零。

  的极点，即无限损耗的频率，位于  轴上，  值由下式给出 其中  表示  的整数部分。我们使用(11)计算  的值，起始三角函数值为  ，然后除以模数  。当  为奇数时，在无穷远处会有  的一个极点。

图6给出了用于执行上述所有计算的Fortran程序（译注，图略）。所有浮点变量，无论是实数还是复数，都是双精度的，并且已被选择以尽可能地反映文本中使用的变量。Matlab 信号处理工具箱中提供了一种非常流行的、用于设计椭圆函数滤波器的商用程序，其函数名为“ellipap”。上述设计方案以阶数、通带波纹  和椭圆模量  作为起始参数，而Matlab程序使用  、  和阻带最小损耗  。用(17)和(35)可以很容易地从  和  计算  ，但是在滤波器设计开始之前，我们必须得到定义了主椭圆函数的模数  。

Matlab程序首先通过算术-几何平均值AGM从  中找到两个四分之一周期  和  。然后使用优化程序找到  ，使其四分之一周期  和  满足(25c)。另一个优化程序步骤用于找到满足(29)的  。参数  和模数的  、  和  函数是通过经典算术-几何平均方法计算的，  的极点几乎可以直接从这些中找到(39)。

最后，通过  的加法定理得到  的复零点，其中  如式(27)；达林顿在他的方程(65)中对此进行了描述[1]。这两个优化步骤相当耗时，并且按照预先设定，将Matlab计算的极点和零点的精度限制为四位或五位。

我们所描述的设计方案，使用带有  作为给定参数的兰登变换，只需进行微小的更改即可接受  来代替  . 就像在 Matlab 程序中一样从  和  计算  ，然后形成  的兰登链，终止于刚好高于浮点算术下限的值。  通过(31)从  中找到，  的兰登链使用(32)反向计算到  ，其中  替换  。因此，  和  的兰登链与以  开头的版本一样可用，而设计的其余部分保持不变。

这种方法以  作为起始设计参数，是在 Matlab 中编程的。该程序(M 文件，ellipap1.m，在图 7 中给出)(译注，图改代码如下，尽管这是20多年前的代码，和现在最新Matlab代码ellipap2比还有约6倍的优势！Matlab代码中是找不到ellipap1的，貌似是对这篇文章致敬)是“ellipap”的直接替代品，但不需要其他子程序，其运行时间比“ellipap”短约80倍，并给出零极点的全精度浮点运算。

% ELLIPAP1 Elliptic analog lowpass filter prototype. % [Z, P, K] = ELLIPAP1(N, Rp, Rs) returns the zeros, poles, and gain % of an N-th order normalized prototype elliptic analog lowpass % filter with Rp decibels of ripple in the passband and a % stopband Rs decibels down. % % This program is a faster and more accurate replacement for % the standard Matlab program ELLIPAP. % % Authors: H. J. Orchard and A. N. Willson, Jr., 9-25-95 % Copyright (c) 1995 % % Reference: % [1] H. J. Orchard and A. N. Willson, Jr., "Elliptic Functions % for Filter Design," IEEE Transactions on Circuits and % Systems-I: Fundamental Theory and Applications, April 1997. function [z, p, k] = ellipap1(n, rp, rs) % special case; for n == 1, reduces to Chebyshev type 1 if n == 1 z = []; p = -sqrt(1/(10^(rp/10)-1)); k = -p; return end dbn = log(10)/20; no = rem(n,2); n3 = (n-no)/2; apn = dbn*rp; asn = dbn*rs; e(1) = sqrt(2*exp(apn)*sinh(apn)); g(1) = e(1)/sqrt(exp(2*asn) - 1); v = g(1); m2 = 1; while v>1e-150 v = (v/(1 + sqrt(1 - v^2)))^2; m2 = m2 + 1; g(m2) = v; end for index = 0:10 m1 = m2 + index; ek(m1) = 4*(g(m2)/4)^((2^index)/n); if(ek(m1)<1e-14), break, end end for en = m1:-1:2 ek(en-1) = 2*sqrt(ek(en))/(1+ek(en)); end % compute poles and zeros for en = 2:m2 a = (1+g(en))*e(en-1)/2; e(en) = a + sqrt(a^2 + g(en)); end u2 = log((1 + sqrt(1 + e(m2)^2))/e(m2))/n; z = []; p = []; for index = 1:n3 u1 = (2*index - 1)*pi/(2*n); c = -1i/cos(-u1+1i*u2); d = 1/cos(u1); for en = m1:-1:2 c = (c - ek(en)/c)/(1 + ek(en)); d = (d + ek(en)/d)/(1 + ek(en)); end af(index) = 1/c; df(index) = d/ek(1); p = [conj(af(index));af(index);p]; z = [-df(index)*1i;df(index)*1i;z]; end if no == 1 a = 1/sinh(u2); for en = m1:-1:2 a = (a - ek(en)/a)/(1 + ek(en)); end p = [p; -1/a]; end % gain k = real(prod(-p)/prod(-z)); if ~rem(n,2) k = k/sqrt(1 + epsilon^2); end end

是否使用  或  作为起始参数取决于个人喜好。阶数  必须是整数的事实意味着满足指标的  的最小值通常会提供一些性能余量，这些余量应该留在  、  和  中。如何最好地做到这一点需要一些工程判断，并且无论采用何种参数选择策略，设计者都需要多次运行程序才能在设计中实现该余量的最佳选择。

VI. 数值示例

我们以一个典型的7阶滤波器作为我们的数值实例，通带纹波为0.1 dB，归一化的阻带边缘频率为  。这给出了模  ，这与我们在第IV节中兰登变换的说明中所使用的值相同。表III首先给出了  的值，通过使用(10)找到和表I中一样的值。

通过式(31)我们可以由  找到  ，其中  。然后使用(32)计算  的值，从  开始，并在表III的  列旁边给出。  是从规定的通带波纹  中找到的，以dB为单位，通过求解(14)得到，其公式为 当  较小时，(40)中的减法会导致一些精度损失。可以通过以下技巧避免这种情况。我们通过乘以  将  从其以分贝(decibel, dB)为单位的给定值改为以奈培(neper)为单位的等效值，现在用  表示这个量，更准确的表达式是  ，然后有 在这里(40)中的减法发生在双曲正弦内部，并且  的大多数子例程将返回完全准确的函数值，而不管  的大小。使用  的值，现在可以使用(37)计算表III中  列。从该列可以看出，  已经达到了限制值。这种行为对于大多数滤波器来说是相当典型的。只有当条件变为需要相对较大的  值(例如，低阶和小阻带损耗)时，我们才会发现  的变化更大。一旦我们有了椭圆函数滤波器的  和  的值，就可以找到(34)所给出的最小阻带损耗，这里是55.43 dB。

下一个主要步骤是计算椭圆函数滤波器的复自然频率。我们首先使用  的极限值和(22)–(24)中的公式找到七阶切比雪夫滤波器的自然频率。表IV给出了-平面上半部分的值，然后使用式(38)和表III中的  ，将这些复零点的倒数一次一个地追溯到模数为0.8的椭圆函数。表V中仅显示了一个零点的倒数(表IV中  时的倒数)的所有这些中间步骤显示为复  。此列中  的倒数是表VI中标记为  列中显示的所需椭圆函数滤波器的-平面上半复零点  的条目。其他零点(包括一个实数零点)的计算以完全相同的方式进行。

最后，(39)中给出的  极点的实  值是通过使用(11)将  转换为  ，然后除以0.8来计算的。  时的极点计算中间步骤如表V右侧  所示。它以  开始并以  结束。这个量除以0.8就是表VI中的  。以同样的方式可以找到其他极点。

读者可能有兴趣将上述计算中的步骤与Gazsi在他的示例4中给出的步骤[7]进行比较。这也适用于7阶滤波器，其中  dB和  。他论文的最终目标是IIR数字滤波器，但他必须首先在  域中设计模拟滤波器。他的计算是针对达林顿描述的设计方法[6]，该方法是基于切比雪夫有理分数的递归。频率被归一化为通带和阻带边缘频率的几何平均值，而不仅仅是通带边缘，这从理论的角度来看很好，但在实际中是个麻烦。这在一定程度上解释了Gazsi变量  和  的出现，而不是使用  和  。

乍一看，达林顿递归似乎只不过是另一种形式的兰登变换。但是进一步研究表明，这是一种更通用的方法，专门用于椭圆函数的情况，并且它的一些公式(但不是全部)与兰登变换的公式略有不同。然而，该方法的更大通用性并未用于允许椭圆函数滤波器的任何推广。达林顿指出他的方案仅限于奇数阶滤波器，尽管它可以很容易地扩展到偶数阶的情况[9]。所涉及的精度和编程量与此处描述的椭圆函数的经典方法大致相同。后者对任何正整数阶都同样适用。

VII. 替代计算方法

尽管前面的部分已经可以根据兰登变换描述了所有需要的计算，但如果没有提及用  函数的替代方法，这篇教程论文将是不完整的，事实证明，该方法已引起了几位作者的注意。  函数是整函数(integral functions)，即，其孤立奇点(singularities)在无穷远处的解析函数。多项式是整函数的最简单示例，具有有限数量的零点。函数  是一个稍复杂的例子，它有无穷多个零，沿实轴均匀分布。  函数更复杂一点，因为它们有一个双周期的零阵列，其值覆盖了整个复平面。对于所有整数  和  ，这些零点在  处，正如在第III节中描述的雅可比函数的极点和零点一样。

与之前一样，参数  可以采用与基本矩形的角S、C、N和D相对应的四个值中的任何一个，这会引导我们按照Neville在[8]中表示的四个不同的  函数那样得到  、  、  和  。函数  在原点处为零，并且那里的导数为1。其他三个  函数在基本矩形的其他三个角之一处都有一个零点，由其下标指定，并且在原点处具有一个常数值1。文献中出现了θ函数的各种归一化，但刘维尔给出的上述似乎是最合乎逻辑的。然后，如果  和  表示  、  、  、  中的任意两个，则雅可比函数  。

即使  函数具有双周期的零点模式，它们作为整函数也不能是双周期的。然而，它们可以是单周期的，并且在经典形式中，它们沿着实轴排列。这允许它们由傅里叶级数表示，奇函数  使用傅里叶正弦级数表示，以及其他三个偶函数使用傅里叶余弦级数表示，这些正弦或余弦的系数仅仅是  的整数幂，如下所示 它将  函数稍微间接地关联到椭圆函数的模  上。对于实数  且  ，也有实数  且  。对于滤波器设计中  的大多数实际值，例如  ，  小于0.23。  的幂，即第  项的系数，是  或  ，这于小值  相结合，导致  函数的傅里叶级数极快地收敛。

我们通过给出其中一个函数的级数来说明  函数的典型形式，即 其中  。如果我们将椭圆函数变量设置为  ，如在第三节的(11)所示，傅立叶级数的基本参数变为  。这展示了与从三角函数端的兰登变换中出现的四分之一周期的固定分数  相同的值。

滤波器指标通常规定模数  ，而不是  ，因此后者必须首先从  中求解，可以通过下式得到 这大约需要与计算  值的兰登链一样多的计算量。

此后，找到由  给出的  的极点，如(39)所示，无论使用兰登变换还是  函数，都需要付出相同的努力，因为这些量都是实数。正是由于在复自然频率的计算，兰登变换显示出其优越性，使用(38)，对于自然频率的倒数具有复  值，它可以像跟踪极点的实数值一样容易地用复数算法从切比雪夫滤波器跟踪到椭圆函数滤波器。在  函数方法中，还没有发现可以直接计算复自然频率的相应可能性。取而代之的是，必须生成许多实椭圆函数，包括一个实数自然频率的特殊情况(或偶数阶情况的等效)，并通过使用  函数的加法定理找到复自然频率，类似于达林顿(Darlington)在[1]中给出的一样。

对  函数方法的细节第一个主要参考可以在1957年由达林顿在贝尔实验室的同事格罗斯曼(Grossman)在[10]中的一篇论文中找到。这项工作仅描述了奇数阶滤波器的情况，这在当时被认为是模拟滤波器所必需的。在Antoniou的一本书[11]中，它已经被推广到涵盖所有整数阶，这是数字滤波器的要求，它提供了一个很好的、易于理解的计算步骤。

Amstutz的另一篇论文[12]讨论了LC梯形滤波器的完整设计，其中包括关于椭圆函数及其计算的部分。在这里，作者对雅可比函数  进行缩放以给出一个函数  ，其定义为 这使得  有一个恒定的虚四分之一周期  和一个实四分之一周期  ，他们分别代替  的  和  。该修改在处理滤波器逼近问题方面具有一些优势，尽管其复杂性是否值得处理非标准椭圆函数是让人怀疑的。

通过使用  的无限乘积，可以计算损耗的极点和复自然频率的所有实椭圆函数，这相当于在虚轴方向上布置周期的  函数，如[13]中所示。如上所述，然后通过加法定理找到复自然频率。兰登变换被简单地提及，但不清楚它是与  的无限乘积一起使用还是代替之。

使用当今的计算机，通过兰登变换或任何这些替代方法计算极点和零点所花费的时间几乎可以忽略不计，并且两者都可以在浮点尾数的最后一位小数位提供几个单位的精度。在过去的50年中，其中一位作者尝试了几乎所有计算椭圆函数的方法，在对  函数[13]产生了最初的热情之后，最终还是决定采用兰登变换。因此，编写这些函数的当前描述是为了自然地引导通过兰登变换对其进行评估，然后将它们用于创建等波纹传递函数。目的是提供对雅可比函数原理的一些理解，而不是“菜谱”式的计算方法。

VIII. 结论

十二个雅可比椭圆函数被认为是最简单的双周期函数，其参数称为模数，用于控制其周期行为。在实际应用中，模数是实数，介于0和1之间。当它为0时，椭圆函数退化为六个单周期三角函数之一，而当它为1时，它们退化为六个单周期双曲函数之一。雅可比椭圆函数的许多性质是这些基本函数之间众所周知的关系的简单推广。

对于模数的任何值，雅可比椭圆函数被可视化为位于一条路径的某个位置，该路径一端为三角函数而另一端为双曲函数。兰登变换允许人们沿着这条路径以离散的步骤移动，并且在这样的步骤前后，与函数值及其模数关联起来的公式非常简单。将具有典型模量的椭圆函数转换到在数值上与三角函数无法区分的点，只需四到五个步骤，然后可以通过将这个三角函数的值沿这条路径逐步转换回模数具有所需值的位置来计算椭圆函数。编制这些计算的程序既简单又准确。这些计算的工具已经被数学家改进了150多年，并且目前已知没有更简单或更好的方法来计算此类滤波器设计中所需的函数。

 

---

审核编辑 ：李倩