深度解析MiddleBurry立体匹配数据集

 

现在，我们知道立体匹配在实际应用中会有各种各样困难的问题需要解决，例如之前提到过的光照、噪声、镜面反射、遮挡、重复纹理、视差不连续等等导致的匹配错误或缺失。于是人们就创造了各种各样的算法来解决这些问题。我们不禁要问一个问题：我们如何公平的比较这些算法的优劣呢？这就是我在这篇文章中想要阐述的内容。让我们先从评价方法的直觉理解开始，然后进入到科学的部分。

一. 视差结果的评价方法

立体匹配里面提到的最基础的固定窗口法的匹配结果：我们可以明显的看到这个视差图中有一些错误，比如台灯支架断裂了，视差图上部分区域是黑色的，还有背景出现不正常的亮区，同时物体的边界和原图的边界似乎无法对应上（比如台灯灯罩等）。但如何量化的说明错误的量呢？如果能够将错误量化，似乎就可以公平的比较各个算法了。我想你也已经想到，要想量化错误，就需要有标准的视差图作为参考，只需要比较算法的结果和标准视差图，并计算不一样的像素的比例，就可以进行评价了。这个领域的先驱们也正是这样做的，其中奠基性的成果就是MiddleBurry大学的Daniel Scharstein和微软的Richard Szeliski在2002年发表的下面这篇文章：作者们提出的第一种评价方案是构造具有理想视差图的参考图像集，并利用下面两大指标来评价各种立体匹配算法的优劣：

1. 均方根误差(RMS Error)，这里N是像素总数

2.错误匹配像素比例除了在整体图像上计算上述两个指标，他们还将参考图像和视差图进行预先分割，从而得到三个特殊的区域，在这些区域上利用上述指标进行更细节的比较。1. 无纹理区域：这是在原始参考图像上计算每个像素固定大小邻域窗口内的水平梯度平均值。如果这个值的平方低于某个阈值，就认为它是无纹理区域。2. 遮挡区域：这个容易理解，在73. 三维重建8-立体匹配4中我介绍了如何获取到遮挡区域，一般可以利用左右一致性检测得到。只不过这里记住是利用参考图像和理想视差值进行计算得到遮挡区域的。3. 深度不连续区域：如果某像素的邻域内像素的视差值差异大于了某个阈值，那么这个像素就位于深度不连续区域内。下面是示意图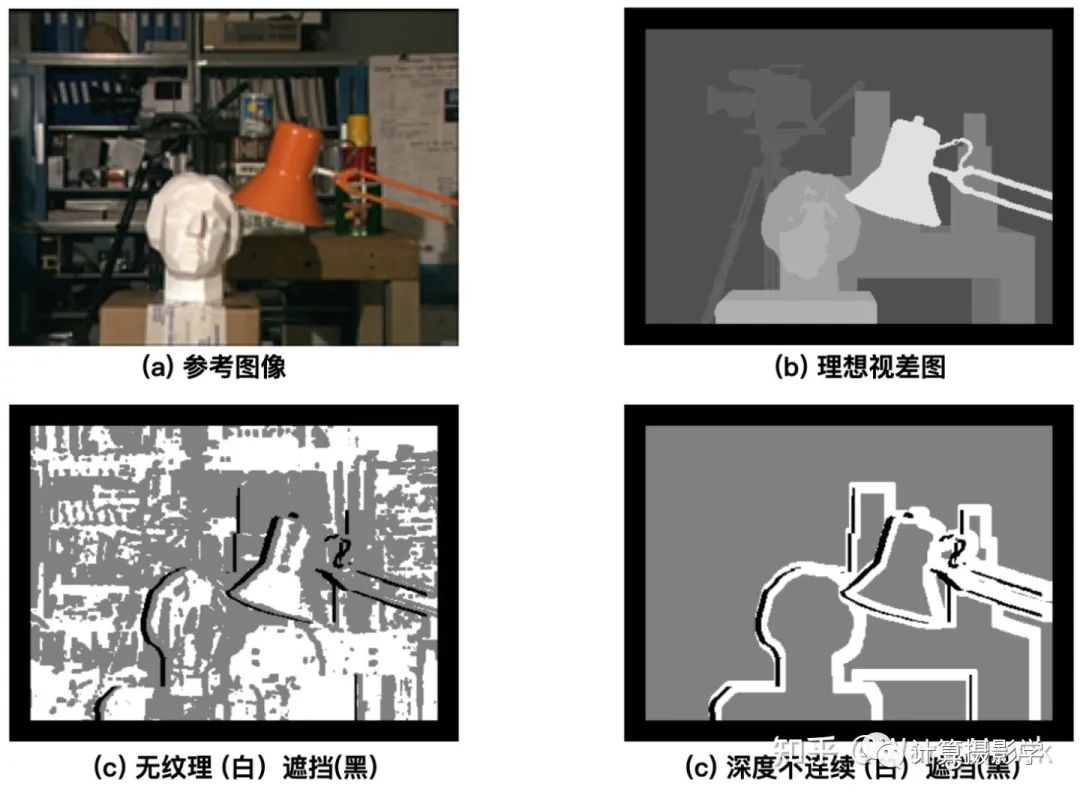：于是作者就会在上面三个区域，以及无纹理区域和遮挡区域的补集，计算均方根误差及错误像素比例这两个指标。作者还指出了评价算法优劣的第二种方案：如果我们有多个视角的原始图像，那么可以通过把原始图像通过视差图进行变换到其它的视角，并和其他视角已知的图像做对比，来量化所谓的预测误差. 这也是一种评价算法优劣的方式，理论上算法计算出的视差图越精准，预测误差越小。比如下面这组图，其中中间是原始参考图像，通过和目标图像一起做立体匹配，可以得到1个视差图。通过此视差图，我们能将参考图像中的点投影到三维空间，然后再投影到不同的视角下。这里左起第1/2/4/5幅图，就是投影的结果，其中第4幅对应原目标图像所在的视角。如果原本在这几个视角有实拍的图像，就可以和投影的结果作对比，对比的结果可以用于计算预测误差。这种方式被作者称为前向变换，图中粉色的像素是在投影后没有信息来填充的像素——这是因为不同视角的遮挡及视差图中的错误导致的。另外一种投影方式被作者称为反向变换。比如下面这组图，中间是原始参考图像。而其他的图像，是在各个视角拍摄的图像通过三维重投影变换到参考图像所在视角后的结果。这里面粉色像素代表因为遮挡导致的无法填充的结果。根据作者描述，反向变换带来的渲染问题更少，更加适合作为计算预测误差所需。所以后面的指标都采用了反向变换。我们总结下作者给出的各种评价指标吧：1. 在全图上计算视差图和理想视差图之间的均方根误差，及错误像素占比2. 在无纹理区域，有纹理区域，遮挡区域，非遮挡区域，深度不连续区域共5个区域计算和理想视差图之间的均方根误差，及错误像素占比3. 在不同视角下进行反向变换，计算变换后的投影误差，即所谓预测误差于是在论文中就有了一张很复杂的表格，主要就在说明我刚提到的几种指标。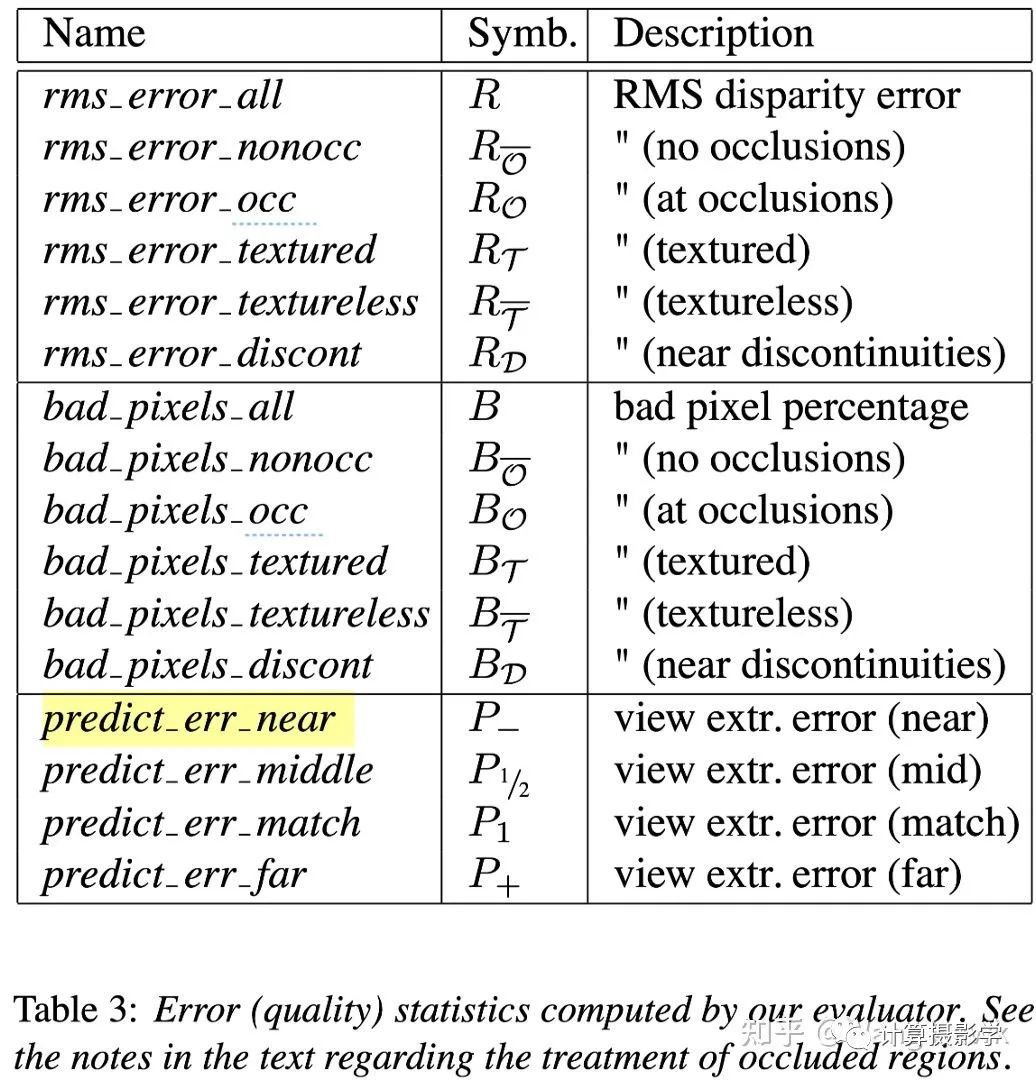各种视差精度评价指标我们很明显能看到，为了计算上述的指标，我们的测试数据集中需要包含下面两类信息中至少一种：1. 输入的两视角原始图像，及对应的理想视差图2. 输入的多视角图像那么，作者是如何构造这样的测试图集呢？

二. 最早期的测试图集(2001年及以前）

在第1节提到的论文中，作者说明了测试数据集的构成，这些数据集就是MiddleBurry立体匹配数据集网站上的2001版数据集。第一类：平面场景数据集在vision.middlebury.edu/s上，你可以看到作者制作的6组平面场景数据。每一组数据由9张彩色图像，和2张理想视差图构成。作者通过将相机摆放在水平导轨上，然后通过移动相机拍摄了这9幅彩色图像，并进行了仔细的立体校正。而视差图则是由第3张和第7张图像进行立体匹配，并分别作为参考图像得到的。这些图像的尺寸比较小，例如Sawtooth的视差图尺寸是434x380像素。我们来看看其中两组图像:Sawtooth及Venus。这里第1列是参考图像，其中作者摆放的都是平面的海报、绘画等，而第2列是对参考图像做手动标记分割为几个部分的结果，属于同一个平面的像素被标为同样的颜色。第3列就是理想视差图。由于现在场景里面都是平面的物体，因此可以通过特征点匹配的方式计算稳定的匹配点对，再利用平面拟合技术，很准确的计算出每个像素的视差。第二组图像是从别的数据集中获得的。这里有Tsukuba大学的著名数据"Head and Lamp"。这组数据有5x5=25张彩色图像，在不同视角拍摄。以中间图像作为参考图像，人工标注了每个像素的视差，下面展示了其中1张视差图。另外还有早期由作者之一Szeliski和另外一位先驱Zabih制作的单色的Map数据集，长下面这个样子。这也是1个平面物体构成的场景，所以理想视差图也用上面提到的平面拟合的方式得到。我们看到，早期的这些数据集都比较简单，而且数量有限。大多数是平面物体构成的场景，像Head and Lamp这样的数据，虽然由人工标注了视差图，但最大视差值比较小，难度较低。尽管如此，这对于当时缺乏标准数据集的立体匹配研究来说，已经是一个里程碑式的事件了。在第一节开篇提到的论文中，作者就是利用这样的数据集和评价指标进行了大量客观的比较，得出了很多重要的结论。

三. 2003年开始，引入结构光技术

正如上一节提出的，2001版的数据太简单了，导致后面一些改进后的算法很容易就能匹配上前述数据集中大多数像素，按照现在流行的说法：过拟合了。于是，前面两位作者采用了新的方法制作更接近真实场景，更加具有挑战性的数据集。这次的数据集主要包括下面两个更加复杂的场景：Cones和Teddy, 你可以看到现在不再是平面目标构成的场景了，而是具有更加复杂的表面特征，以及阴影和更多深度不连续的区域。不仅如此，此次提供的图像的尺寸也很大，完整尺寸是1800x1500，另外还提供了900x750及450x375两种版本。同时，还包括了遮挡区域、无纹理区域、深度不连续区域的掩码图像，用于各种指标的计算。Cones:Teddy:在2003年CVPR中他们发表了下面这篇文章，阐述了新数据集的制作方法：我们从标题就可以看出，这次他们采用了结构光技术自动的计算出每组图像的高精度稠密视差图作为理想参考。下面是他们的实验设置。这里采用的相机是Canon G1，它被安装在水平导轨上，这样就可以以固定间隔移动拍摄不同视角的图像，对于同一个场景作者会拍摄9个不同视角的图像，并用其中第3和第7张来产生理想视差图。与此同时，有1个或多个投影仪照亮场景。比如在拍摄Cones场景时，就用了1个投影仪从斜上方照亮场景，这样大部分区域都可以照亮，除了画面右上方的格子间有一些阴影，由于阴影前方是平面的栅格，所以这些阴影区域的视差值能够通过插值算法恢复出来。而在拍摄Teddy场景时，则是采用了两个投影仪从不同的方向打光照亮场景，尽量减少阴影。不过，由于Teddy场景更加复杂，即便是用了两个方向的照明，依然会有少量的区域位于阴影中（没有任何1个投影仪能照亮），使得这些区域的视差不可知。这里面，投影仪会按次序发出N个结构光图像照亮场景，相机则把这一系列图像拍摄下来。注意看论文中的示意图。这里用到的是一种叫做格雷码的图案(Gray-Code)，是一种黑白条纹图案。为了理解作者是如何获取高精度视差图的，我们需要先理解下结构光三维重建的原理。这里我用投影仪发出最简单的黑白条纹图像来做一点点介绍，之后我会写更详细的文章来介绍结构光三维重建。我们看下面这个场景，投影仪向场景按时间顺序投出7个图像，并被相机拍摄下来。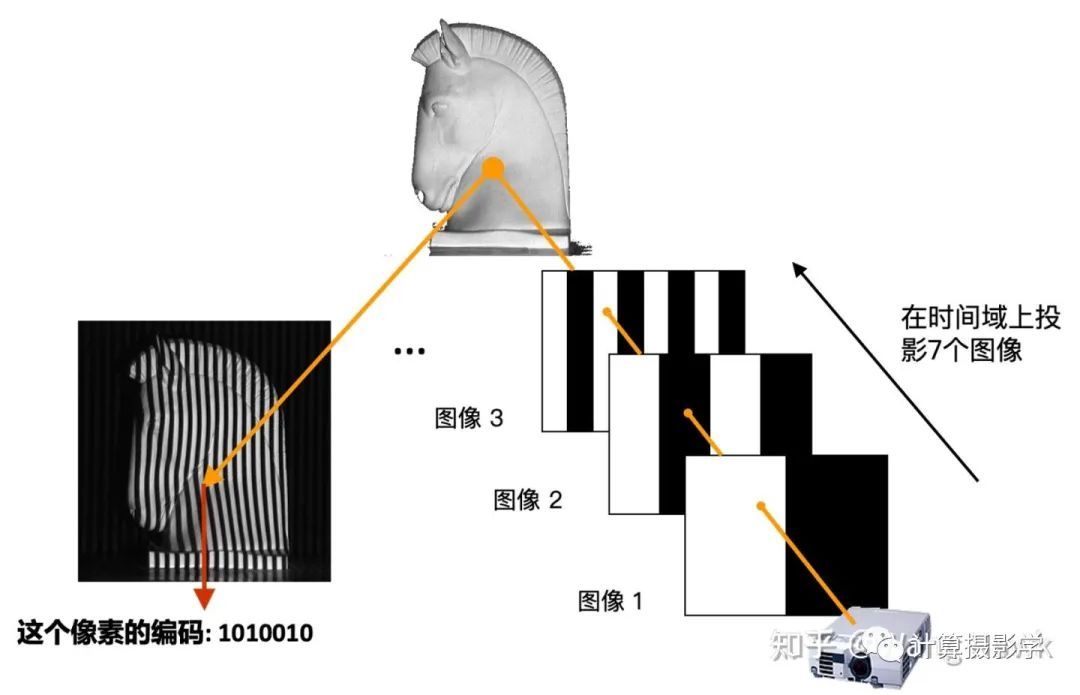拍下来的系列图像是这样的：我们在时空两个维度上观察接受到的图像，就会发现每个场景位置处的信息形成了独特的编码。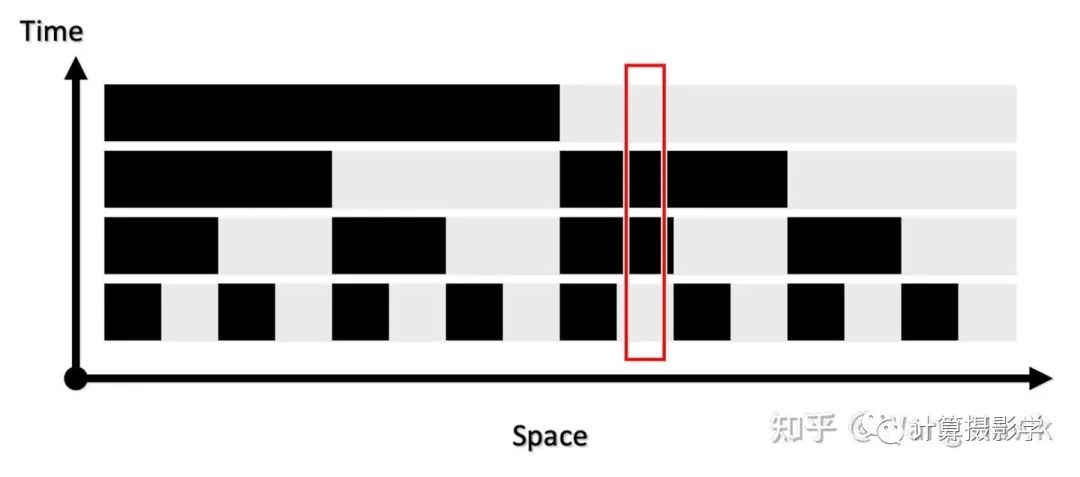比如上面箭头所指像素的编码就是1010010，而且在两个视角下对应像素的编码是一致的，这就给了我们精确寻找两个图像的对应像素的方法——我们只需要寻找相同编码的像素即可。这里编码有7位，意味着我们可以为128列像素指定不同的编码。如果再发出的是水平条纹，那么可以为128行像素指定不同的编码。这样，就可以支撑尺寸为128x128的像素阵列的视差计算了。如果编码长度变为10位，那么就可以支持精确计算出1024x1024的视差图。现在我们回到Daniel Scharstein和Richard Szeliski的研究，他们确实是采用了类似原理，通过发出水平和垂直的条纹结构光来精确的寻找两个视角下图像间的对应关系的。作者用的投影仪是Sony VPL-CX10，投出的图案是1024x768像素，所以用10位编码足够了，也就是投出10个水平序列图案和10个垂直序列图案。下面展示了其发出的水平和垂直结构光经过阈值分割后的黑白条纹的状态。通过这种方法，就可以得到精确的视差图了，作者把此时得到的视差图称为View Disparity。这个过程可以图示如下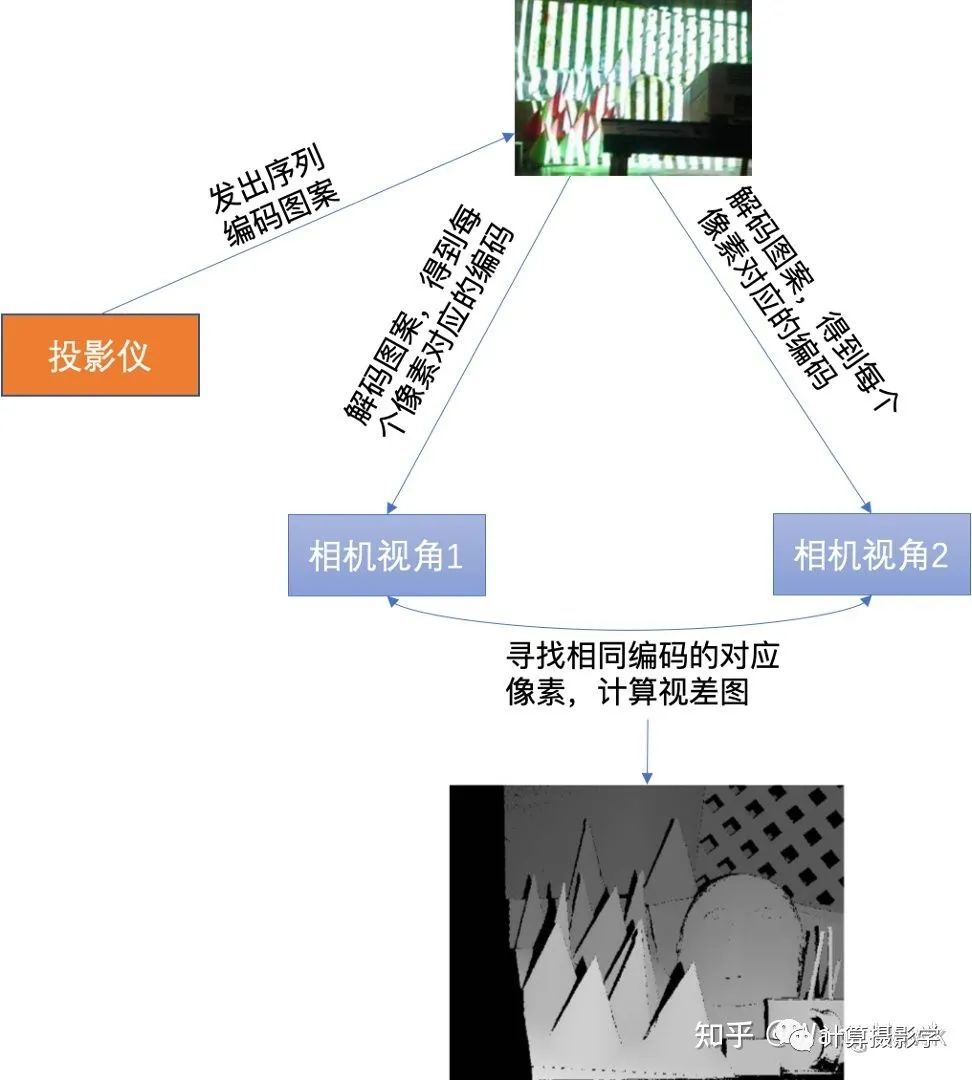：你可以看到，View Dispariy中存在大量的黑色像素，这是怎么回事呢？这里主要由这么几种情况导致：

1. 遮挡，部分像素只在1个视角可见，在另外1个视角不可见
2. 阴影或反射，导致部分像素的编码不可靠，使得匹配失败。
3. 在匹配时，因为相机分辨率和投影仪分辨率不一致，因此所需的插值或者混叠导致了一些像素无法完美匹配，从而在左右一致性检查时失败。
4. 同样，因为投影仪分辨率不足，导致相机成像时多个像素对应同一个投影仪像素。这可能导致一个视角下的1个像素可能和另外一个视角下多个像素匹配上，从而在左右一致性检查时失败。
5. 还有，就是当采用多个不同的光源方向时，不同光源方向照明时得到的视差图不一致。这种不一致的像素也会被标记为黑色像素。

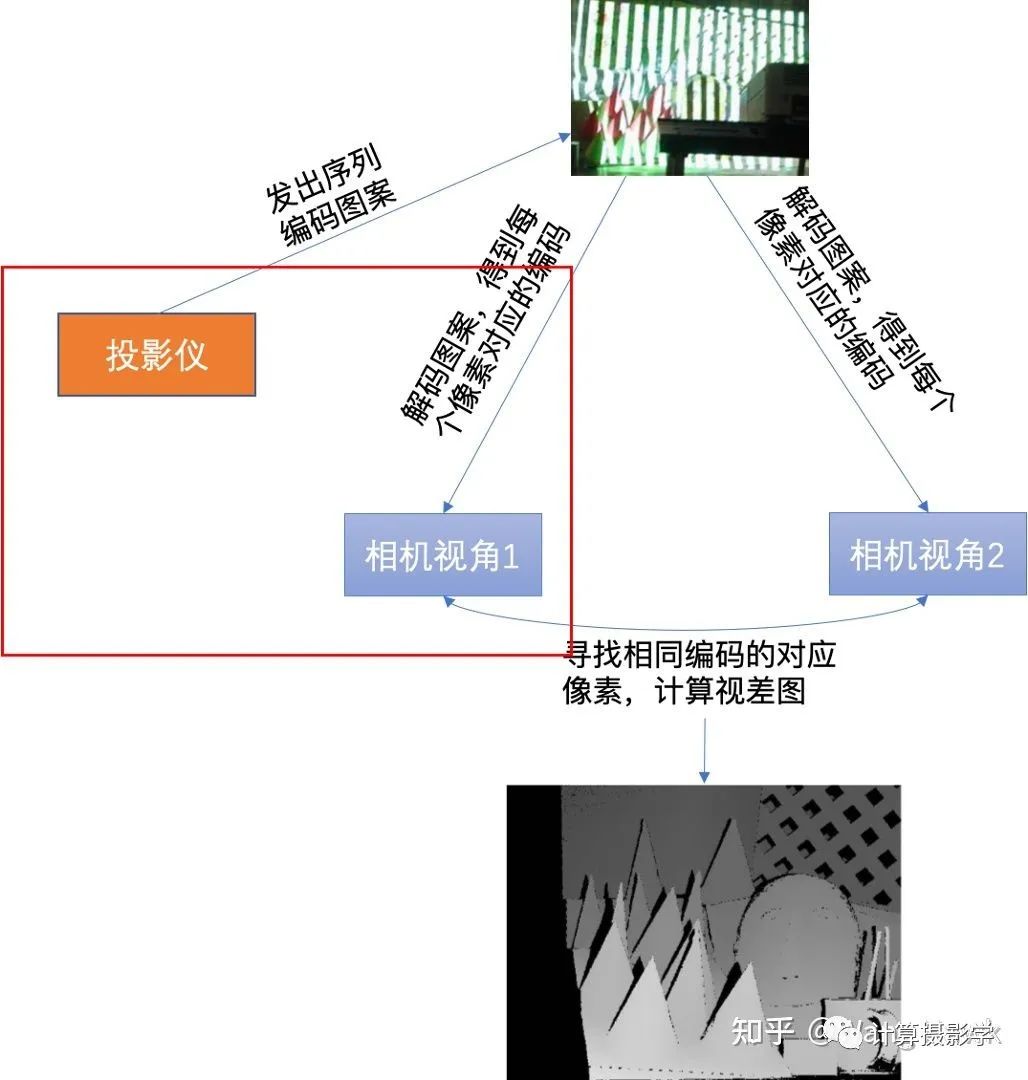很显然，这样的视差图是不足以作为理想的视差图的。我们理想中的视差图，需要绝大多数像素都有准确的视差值，那么该如何做呢？我们来看看刚才这张图上的这个部分：这里，我们注意到当相机视角1下的图像点和投影仪上的图案点之间是有明显的投影关系的。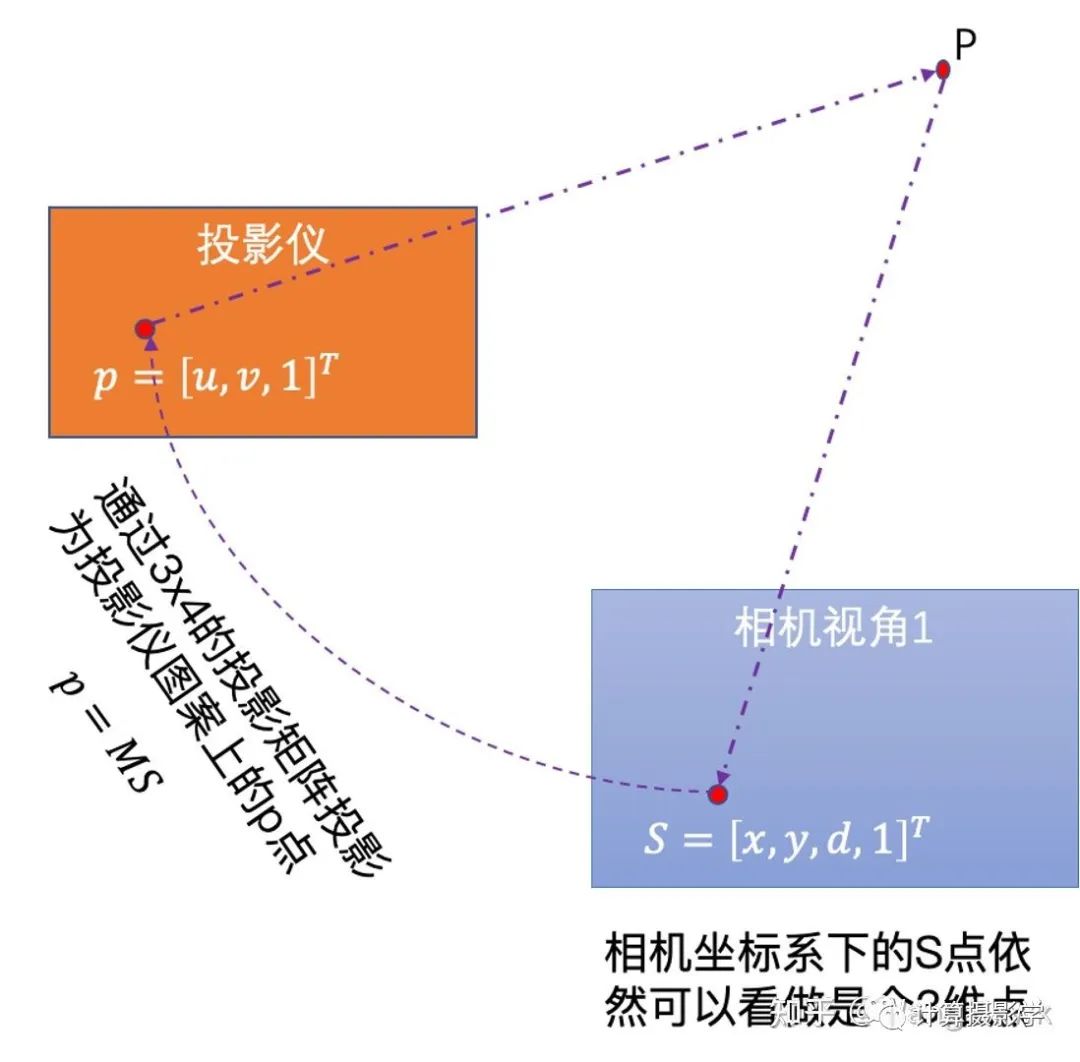我们有大量的通过前述过程已知视差值d的像素点，因此可以按照上图建立起超定方程组，并用迭代式的方式求取稳定的投影矩阵M。当M已求得后，就可以将M当成已知量，再次套用p = MS这个式子，求得每个像素的视差值——即使这个像素在此前的view disparity计算过程中因为种种原因被标为了黑色也没关系，只要投影仪能够照亮的像素都可以计算出一个视差值，作者把这种方式计算出来的视差值称为illumination disparities。由于1个投影仪可以和左右相机都计算出这样的视差图，所以我们可以得到2张illumination disparity图。下面是个示例图，(a)是拍摄的序列图像中的一张，(b)是参考图像的所谓View Disparity (c)就是Illumination disparitiy。你可以看到，这里标为黑色的像素明显少了很多，大部分都是投影仪无法照亮的像素。(d）则是将(b)和(c)合并的结果。如果有多个投影仪，那么每个投影仪都可以计算一次对应的Illumination Disparity，而且是左右图都可以计算出自己的Illumination Disparity，最后将所有计算出的视差图合并起来即可。如果我们有N个投影仪，那么对应于左图的右图共有2N个Illumination Disparities，再加上view disparities 2张，一共就需要合并2N+2张视差图。比如Teddy场景，有两个投影仪，就会有6张视差图需要合并，下图是示例，展示了部分视差图和最终合并的结果。通过上述过程，就可以得到精度非常高的视差图了，这就会被作为最终的理想视差图。Daniel Scharstein和Richard Szeliski采用的这个方案精度非常高，非常适合制作立体匹配的理想参考数据集，于是2005年，MiddleBurry的Anna Blasiak, Jeff Wehrwein和Daniel Scharstein又用此方法构造了更多高精度的数据集，共9组，下面是一些例子，我想很多人都看到过第1组。这次采集数据时，每组数据有7个视角，3种照明，还有3种不同的曝光设置。视差图基于第2视角和第6视角计算，完整的图像尺寸大概在1300x1100。这个数据集相比之前的数据集更加有挑战性，因为图像中包括了更大的视差，更多的平坦区域。到了2006年，还是MiddleBurry大学，Brad Hiebert-Treuer, Sarri Al Nashashibi 以及 Daniel Scharstein一起又制作了21组双目数据。跟2005年一样，依然是7个视角，3种照明，3种曝光设置。这次的完整图像尺寸大概是1380x1100。这次的数据很多人都看过，比如下面几张就非常出名。我们可看到，这些数据是越来越有挑战性，具有丰富的种类，且更多困难的区域，非常适合对各种立体匹配算法进行量化的评价。

四. 2014年，更加复杂的制作技术

前面讲的数据集在立体匹配的研究中起了非常大的作用，很多重要的方法都是在这时候的数据集上进行评价和改进的。然而，它们的数量有限，场景有限，人们认识到需要更多更复杂的场景，来促进立体匹配算法的进一步改进。于是，2011年到2013年间，MiddleBurry大学的Nera Nesic, Porter Westling, Xi Wang, York Kitajima, Greg Krathwohl, 以及Daniel Scharstein等人又制作了33组数据集，2014年大佬Heiko Hirschmüller完成了对这批数据集的优化。他们共同在GCPR2014发表了下面这篇文章，阐述了这批数据集的制作方案：我截取几组图像如下，其中很多都是在立体匹配研究中经常用到的出名的场景，比如我就特别喜欢图中那个钢琴那么，这次的数据集制作方法相比以前的有什么贡献呢？主要有下面这几点：1. 作者采用的是可移动的双目系统，包括两个单反相机，两个数码相机，以及相应的导轨和支架构成。这样就可以在实验室外拍摄更加丰富的场景。所以最后的数据集里面就包括了各种各样丰富的、更加真实的场景。而且，这次作者的光照条件更加丰富，有4种，而曝光设置则有8种。为了能够重现照明情况，还单独拍摄了环境图像。下面是论文中的一个示意图，你可以看到，摩托车表面可能会有高反射区域，为了能够准确的获取这些区域的理想视差图，作者在车身表面喷涂了特殊的材质，我想应该是为了减少反光，使得匹配能成功。2. 更加复杂的处理流程，得到高精度的数据集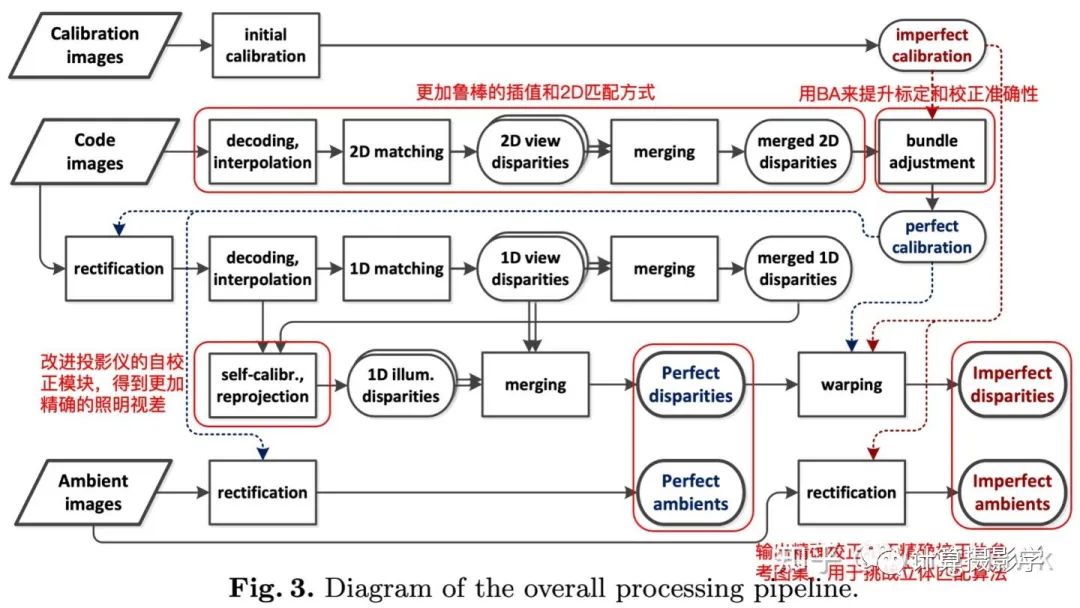：这里我们看到：1. 2003年的方法没有很好的处理标定和校正带来的误差，事实上这样的误差会影响到最终生成的理想视差图的精度。这里的新方案采用了Bundle Adjustment来减小标定和校正的误差，进一步提升了精度。2. 相比2003年的方法，这里采用了更加鲁棒的方式来解码结构光信息，并用更好的方法来进行2D匹配，这样就可以更准确的进行立体校正。在采用了这两个优化点后，立体校正的精度和稳定性都提升了很多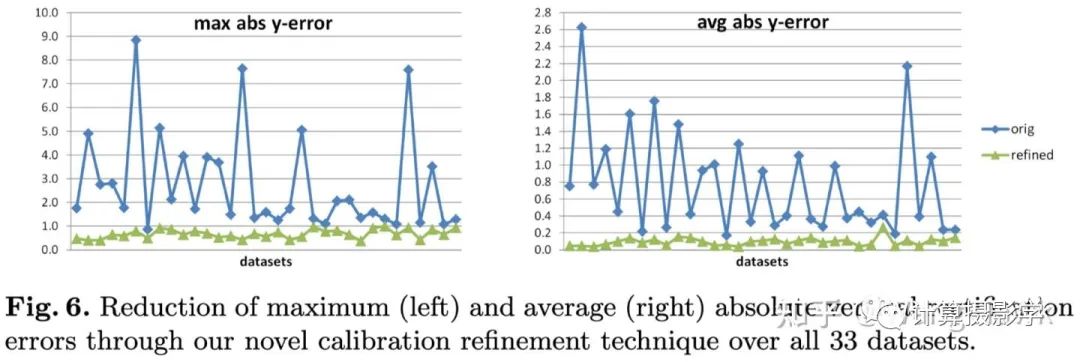：3. 前面我们提到了Illumination Disparity(照明视差)很重要，因此这里引入了更好的自校正模块，可以得到更好的照明视差4. 另外，为了挑战立体匹配算法在输入图没有精确rectify的表现，这里还输出了两种图集。一种是经过精确rectify的，保证满足对极线水平对齐。另外一种则是没有经过精确rectify的，对算法的挑战更大。  因为篇幅原因，我就不详细暂开讲解了。总之，这33组数据集中，10组释放出来供大家做训练，10组用于测试(理想视差图未公开)，其他的数据用于公开研究。这些数据完整的尺寸甚至达到了3000x2000，最大视差有达到800像素的！不仅仅如此，在MiddleBurry官网上还提供了完善的工具，可以加载、评估、分析这些数据，可以在此处访问：vision.middlebury.edu/s比如其中有个叫plyv的工具，实现了视角合成功能，便于我们可以从各个视角来观察场景：

五. 2021年，增加用移动设备拍摄的数据集

之前的数据集都是用单反相机作为主要成像设备的，因此图像的质量非常高。2019年到2021年间，Guanghan Pan, Tiansheng Sun, Toby Weed, 和Daniel Scharstein尝试了用移动设备来拍摄立体匹配数据集。这里他们采用的是苹果的iPod Touch 6G，它被安装到一个机械臂上，在不同视角下拍摄场景。视差图的生成还是用了上一章介绍的方法，只不过做了适当的裁剪。这批数据一共24组，每个场景会有1到3组数据，下面是例子：不过我看这里的视差图依然是用较大差异的两视角生成的，对于当今手机上的小基距双摄系统来说，这个数据集的参考价值没有那么大，毕竟当前手机上的两个摄像头之间基距大概就10mm左右，与这里的情况差距较大。

六. 总结

这篇文章里，我为你介绍了几种核心的立体匹配评价指标，以及MiddleBurry大学的几代立体匹配数据集的制作方式。现在做相关研究的人确实应该感谢包括Daniel Scharstein、Richard Szeliski和Heiko Hirschmüller在内的先驱们，他们创建的MiddleBurry立体匹配数据集及评价系统极大地推动了这个领域的发展。到了今年，一些计算机视觉界的顶会论文依然会描述自己在MiddleBurry 立体匹配数据集上的评价结果。目前排名第1的算法是旷视研究院今年推出的CREStereo，相关成果也发表到了CVPR2022，并会做口头报告，我之后如有时间也会撰文加以讲解。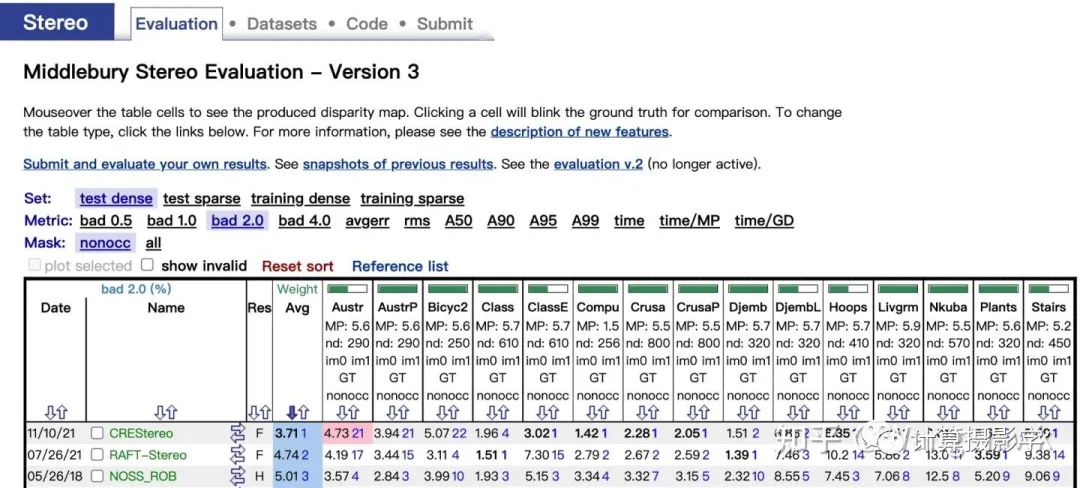总之，立体匹配算法要继续发展，需要大量符合真实场景复杂性的高精度数据集，我们学习前人的做法，是为了能够找出更好的方法，制作更多的数据。我还会在接下来的文章中，给你介绍其他著名的数据集，敬请期待。

七. 参考资料

1、MiddleBurry双目数据集2、D. Scharstein and R. Szeliski. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms. International Journal of Computer Vision, 47(1/2/3):7-42, April-June 20023、D. Scharstein and R. Szeliski. High-accuracy stereo depth maps using structured light. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2003), volume 1, pages 195-202, Madison, WI, June 2003.4、D. Scharstein and C. Pal. Learning conditional random fields for stereo. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2007), Minneapolis, MN, June 2007.5、H. Hirschmüller and D. Scharstein. Evaluation of cost functions for stereo matching. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2007), Minneapolis, MN, June 2007.6、D. Scharstein, H. Hirschmüller, Y. Kitajima, G. Krathwohl, N. Nesic, X. Wang, and P. Westling. High-resolution stereo datasets with subpixel-accurate ground truth. In German Conference on Pattern Recognition (GCPR 2014), Münster, Germany, September 2014.7、CMU 2021 Fall Computational Photography Course 15-463, Lecture 18

 

 

审核编辑 ：李倩