信号处理中相关与卷积的区别

 

信号的相关

相关是表征两个信号之间（互相关）或者一个信号相隔一定时间的两点之间（自相关）相互关联的程度。

 

相关的性质

共轭对称性；

自相关函数在原点的值等于信号能量；

相关函数的面积等于信号面积模的平方；

复信号s(t)自相关函数的傅里叶变换是正实函数；如果二个信号在频域上具有相同的能谱，在时域上具有不同的波形，但是这二个信号的相关函数却相同。

 

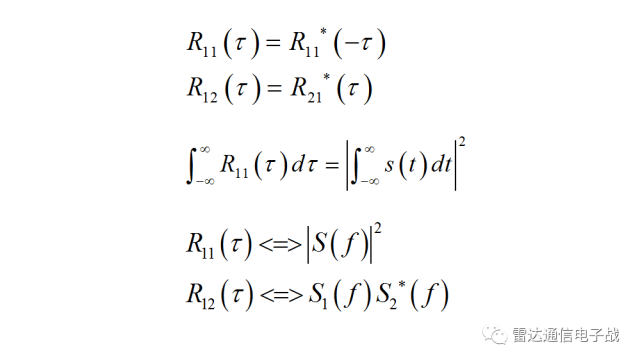
信号的卷积

卷积是两个时间序列之间一种激励和响应得出结果的关系。 卷积是可交换，可结合和可分配的。

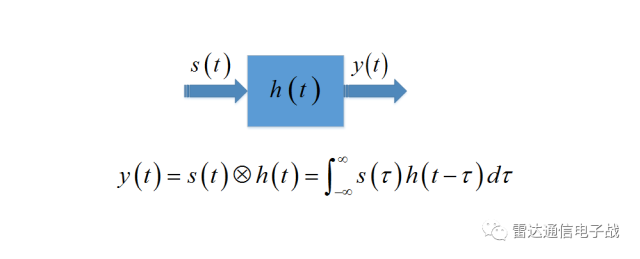
将一个时间信号作为输入序列，另一个信号作为系统的响应。这种响应是非因果的，即不仅要考虑某一时刻输入信号的响应，还要全部包含这之前所有输入的响应。卷积运算具体的计算过程如下图。

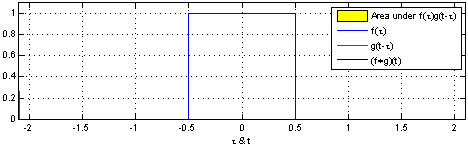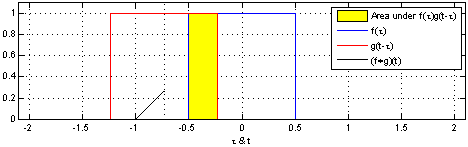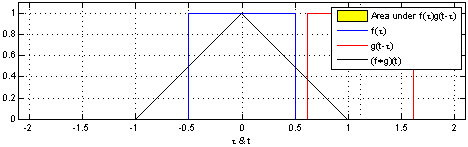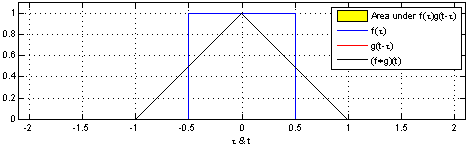
相关积分和卷积积分值有限，都要求二个信号中至少有一个是能量有限信号。当二个信号都为功率信号时，积分结果是无限的，需引入时间平均。 

相关与卷积的区别

相关运算中被积函数没有时间反褶的过程，而卷积运算中有。

相关函数不满足交换，而卷积可以。

相关公式和卷积公式很像，相关能利用卷积表示，所以有人就觉得两个概念有关系，其实二者从概念上没有联系。

 

Matlab中相关和卷积的函数

Cross-correlation and Autocorrelation（互相关与自相关） ：r=xcorr(x,y) 

Convolution（卷积） ：w=conv(u,v) 

  编辑：黄飞