
资料下载

使用引力子和电子自旋量子比特的1位可逆RAM
描述
1 位时间可逆 RAM
我已经使用量子门制作了一个 1 位 RAM 的基本电路。输入 A 充当 SR 触发器的 S。输入 B 是写使能线。输入 R 是读使能线。当启用写使能线时,我们可以写输入。当我们激活读使能线时;我们可以读取写入的输入。现在,这些数据可以通过量子隐形传态瞬间传输到另一个 RAM 位置。
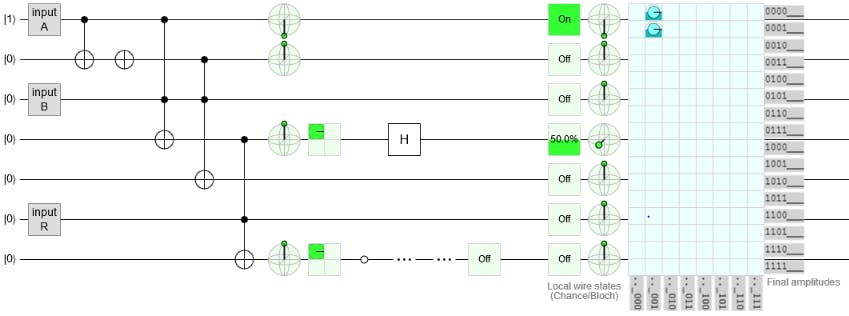
您可以在矩形交叉表之前的最左下角看到输出。它现在关闭,因为读取启用和写入启用线均未激活。
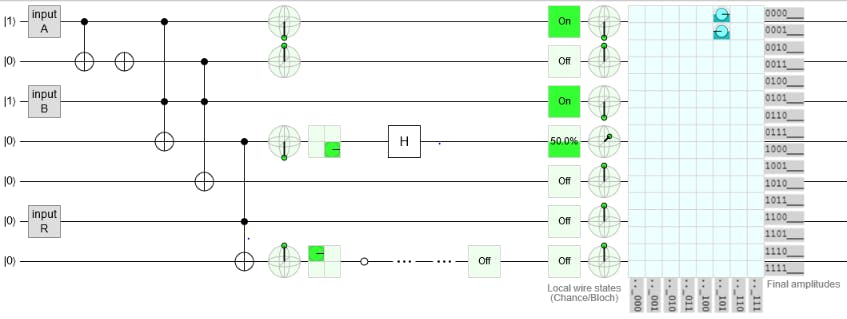
现在在上图中,写使能线被激活,因此输入被存储;但是当我们可以看到写入启用输出线上的叠加时,因为我已经放置了一个 Hadamard 门;因为它完全是读取启用行的工作,为我们提供存储的值。
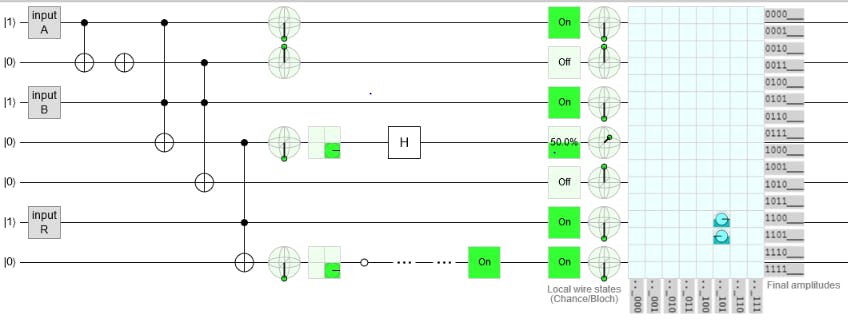
现在如您所见;因为读使能线被激活;我们可以看到输出----- 为 1。因此我们使用 Qubits 制作了一个 1 位 RAM。免责声明 - 该电路仅在上下 Qubits 的情况下工作 100% 准确;对于随机叠加;结果并不总是准确的。目前正在从事这方面的工作。
现在我们可以使用量子隐形传态将这些信息传输到另一个 RAM 单元---------- 数据总线的修改;我将在下一部分详细讨论。我将讨论如何使用量子纠缠和量子隐形传态来制作量子数据总线。
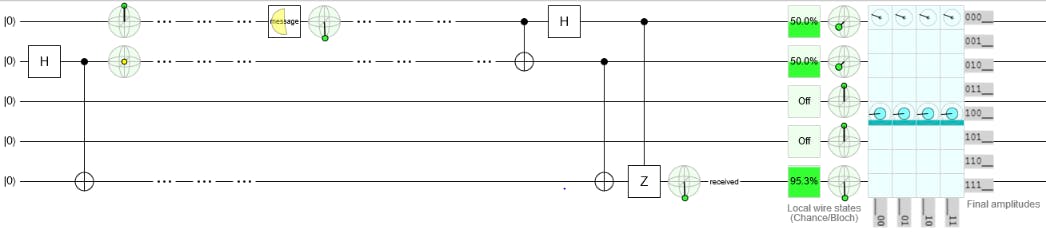
这是量子隐形传态的电路。在这里查看我的量子隐形传态模型的模拟:
使用电子自旋产生量子比特:
我们可以使用 Stern-Gerlach 实验的程序制作自旋量子比特。
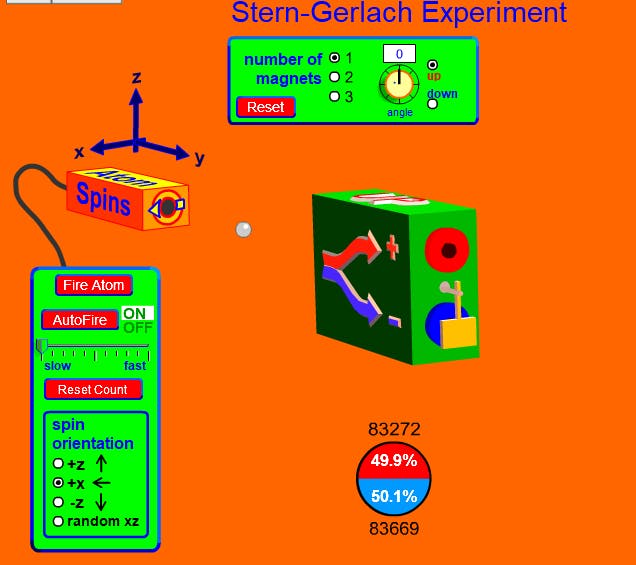
随着叠加自旋(+x 自旋)轰击电子数量的增加;向上旋转和向下旋转的概率为 50 -50。向上自旋偏向正极,向下自旋偏向负极。我们可以将这些自旋视为量子比特。因此,我们可以使用电子自旋轻松生成量子比特。你可以从这里得到一个直观的想法:
使用引力子生成量子比特:
现在让我们来到引力子部分。在研究弦论时,我对粒子引力子很着迷。出色地 ; 在传统的量子计算中;光子的极化被用作量子比特。一个有趣的事实是,引力子实际上是两个沿同一方向旋转的光子。因此,它比光子携带更多信息。对于 N 个引力子来说,这就是 4^N 位信息。

上图是康奈尔大学一篇论文的摘录,该论文强调如何从两个光子轻松制备引力子。
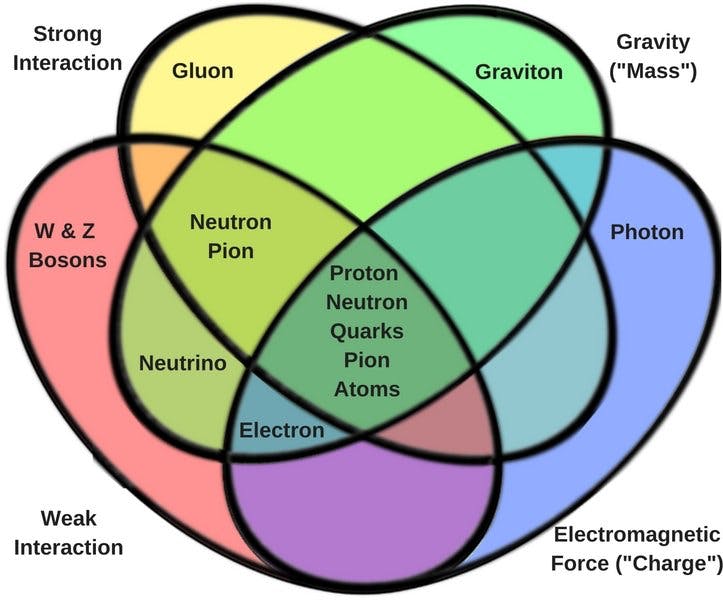
如果我们考虑光子;它通过特定的水晶;将其分成两个极化;我们可以将水平和垂直极化视为我们的两个量子比特。任何随机极化只是水平和垂直极化的叠加。同样,我们可以使用引力子来生成量子比特。我将谈论这个关于引力子的话题,以及量子纠缠如何揭示平行宇宙;在本系列的后面部分。希望您喜欢这一系列的 Digital TENET。
谢谢
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






