大规模3D重建的Power Bundle Adjustment

大规模 3D 重建的Power Bundle Adjustment

笔者个人理解

我们知道BA问题本质上是求解增量线性方程的方程，在BA中H矩阵有着其特殊的结构

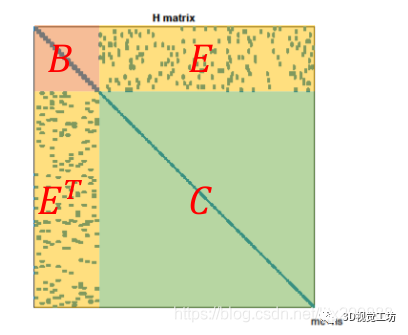
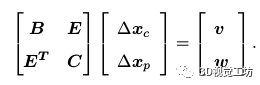
其中B，C是对角块矩阵，C的规模远大于B，对角块矩阵求逆的难度远小于普通矩阵，故而我们可以将其简化为

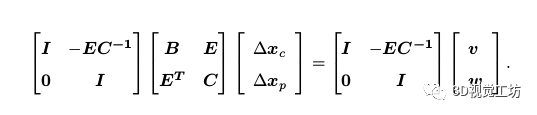
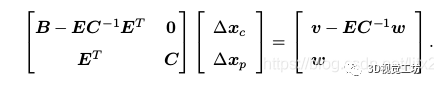
这样第一行方程就变为与xp无关的项

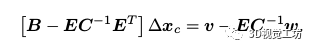
求解出，代入到第二个方程，利用C矩阵易于求逆的性质，快速求解出。

很明显，在整个过程中耗时最多的便是求解Schur 补消元后的第一个方程。在这篇论文中作者提出了利用幂级数的方法来加速求解第一个方程，下面可以和笔者一起来看一下具体的实现方式。

摘要

我们引入 Power Bundle Adjustment 作为一种扩展型算法，用于解决大规模BA问题。它基于逆 Schur 补的幂级数展开，构成了我们称之为逆展开方法的新求解器家族。我们从理论上证明了幂级数的使用是正确的，并且证明了我们方法的收敛性。使用真实世界的 BAL 数据集，我们表明所提出的求解器挑战了最先进的迭代方法，并显着加快了法方程的求解速度，即使达到了非常高的精度。这个易于实施的求解器还可以补充最近提出的分布式BA框架。我们证明，使用建议的power BA作为子问题求解器可以显着提高分布式优化的速度和准确性

1、介绍

BA （BA） 是一个经典的计算机视觉问题，它构成了许多 3D 重建和运动结构 （SfM） 算法的核心组成部分。它指的是通过最小化非线性重投影误差来联合估计相机参数和 3D 地标位置。最近出现的大规模互联网照片集 ［1］ 提出了对在运行时和内存方面可扩展的 BA 方法的需求。为增强现实或自动驾驶等应用构建准确的城市比例地图使当前的 BA 方法达到了极限

由于正规方程的求解是 BA 中最耗时的步骤，因此通常采用 Schur 补技巧来形成缩减相机系统（RCS）。这个线性系统只涉及位姿参数并且明显更小。通过使用 QR 因式分解，仅导出 RCS 的矩阵平方根，然后求解代数等价问题 ［4］，可以进一步减小其大小。RCS 及其平方根公式通常通过迭代方法求解，例如针对大规模问题的流行预处理共轭梯度算法，或通过直接方法（例如针对小规模问题的 Cholesky 分解）求解

在下文中，我们将依靠逆 Schur 补的迭代逼近来挑战这两个求解器系列。特别是，我们的贡献如下：

• 我们为高效的大规模 BA 引入了power BA （PoBA）。我们称之为逆扩展方法的这一新技术系列挑战了建立在迭代和直接求解器上的最先进的方法。

• 我们将boundle adjustment问题与幂级数理论联系起来，我们提供了证明这种扩展合理的理论证明，并建立了求解器的收敛性。

• 我们对BAL 数据集上提出的方法进行了广泛的评估，并与几个最先进的求解器进行了比较。我们强调了 PoBA 在速度、准确性和内存消耗方面的优势。图 1 显示了 97 个评估的 BAL 问题中的两个的重建。

• 我们将我们的求解器合并到最近提出的分布式 BA 框架中，并在速度和准确性方面显示出显着的改进。

• 我们将求解器作为开源软件发布，以促进进一步研究。

2、相关的工作

由于我们提出了一种求解大规模BA的新方法，我们将回顾BA和传统求解方法，即直接法和迭代法的工作。我们还提供了一些关于幂系列的背景知识。关于级数扩展的一般介绍，我们请读者参考［14］。

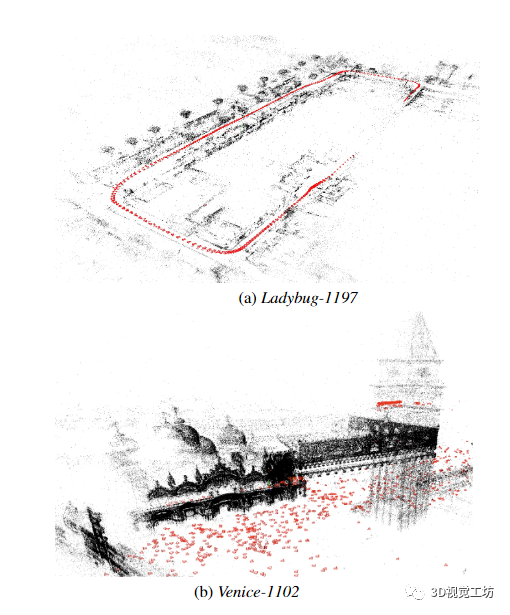
图 1. Power Bundle Adjustment （PoBA） 是一种针对大规模 BA 问题的新型求解器，它比现有求解器速度快得多，内存效率更高。（a） 具有 1197 个姿势的瓢虫 BAL 问题的优化 3D 重建。PoBA-32（分别为 PoBA-64）比最佳竞争求解器快 41%（分别为 36%）以达到 1% 的成本容差。（b） 具有 1102 个姿势的 Venice BAL 问题的优化 3D 重建。PoBA-32（分别为 PoBA-64）比最佳竞争求解器快 71%（分别为 69%）以达到 1% 的成本容忍度。PoBA 的内存消耗是√BA（resp. Ceres）的五倍（resp.两倍）。

2.1可扩展的boundle adjustment

boundle adjustment的详细调查可以在 ［16］ 中找到。Schur 补码 ［20］ 是利用 BA 问题稀疏性的普遍方法。分辨率方法的选择通常由正规方程的大小决定：随着大小的增加，稀疏和密集 Cholesky 分解 ［15］ 等直接方法的性能优于不精确牛顿算法等迭代方法。具有数万张图像的大规模BA问题通常通过共轭梯度法 ［1， 2， 8］ 来解决。已经设计了一些变体，例如可以扩大搜索空间 ［17］ 或可以使用基于可见性的预调节器 ［9］。最近一系列关于平方根BA的工作建议用零空间投影 ［4、5］ 代替 Schur 补码来消除地标。它导致显着的性能改进，并在速度和准确性方面成为boundle adjustment问题的最佳性能求解器之一。尽管如此，这些方法仍然依赖于传统的求解器来解决减少的相机系统问题，即用于大规模 ［4］ 的预处理共轭梯度法 （PCG） 和用于小规模 ［5］ 问题的 Cholesky 分解，此外还有一个重要的成本内存消耗术语。即使使用 PCG，求解正规方程仍然是瓶颈，找到数千个未知参数需要大量的内部迭代。其他作者试图通过关注高效并行化 ［13］ 来提高 PCG BA 的运行时间。最近，随机 BA ［22］ 被引入以将减少的相机系统随机分解为子问题，并通过密集分解求解较小的正规方程。这导致了具有改进的速度和可扩展性的分布式优化框架。通过将一般幂级数理论封装到线性求解器中，我们建议同时提高这些现有方法的速度、准确性和内存消耗。

2.2幂级数求解器。

虽然幂级数展开常用于求解微分方程 ［3］，但据我们所知，它从未用于求解BA问题。最近的一项工作 ［21］ 将 Schur 补码与 Neumann 多项式展开联系起来，以构建一个新的预条件器。尽管这种方法对某些物理问题（例如对流扩散或大气方程）给出了有趣的结果，但它对于BA问题仍然不能令人满意（见图 2）。相反，我们建议直接应用逆 Schur 补的幂级数展开来解决 BA 问题。因此，我们的求解器属于扩展方法的范畴——据我们所知——从未应用于 BA 问题。除了是一个易于实现的求解器之外，它还利用 BA 问题的特殊结构来同时提高现有方法的权衡速度精度和内存消耗

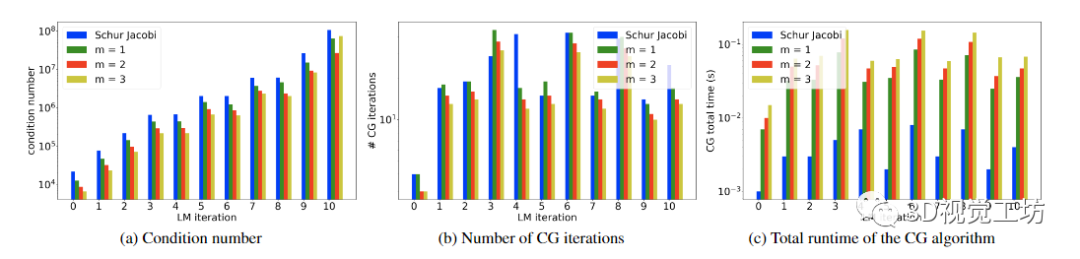
图 2. 尽管 ［21］ 探讨了使用幂级数作为某些物理问题的预条件子，但它受到 BA 公式的特殊结构的影响。给定预处理器 M -1 和 Schur 补码 S，条件数 κ（M -1S） 与共轭梯度算法的收敛性相关联。（a） 说明了 LM 算法针对实际问题 Ladybug-49 的第 10 次迭代的行为，其中具有来自 BAL 数据集的 49 个姿势，并且对于用作 CG 算法预条件子的幂级数展开 （22） 的不同阶数 m 。与流行的 Schur-Jacobi 预条件子相关的条件数通过这个幂级数预条件子减少了，这通过 CG 算法更好的收敛和更少的 CG 迭代次数 （b） 来说明。然而，由于幂级数预条件器的应用涉及 4m 矩阵向量乘积，因此每个补充阶 m 在运行时方面的成本更高，而 Schur-Jacobi 预条件器可以有效地存储和应用。（c） 导致求解正规方程 （6） 时的总运行时间增加。

3、幂级数

我们简要介绍矩阵的幂级数展开。令 ρ（A） 表示方阵 A 的谱半径，即最大绝对特征值，并用‖A‖ = ρ（A） 表示谱范数。以下命题成立

命题 1. 令 M 为 n × n 矩阵。若M的谱半径满足‖M‖《1，则

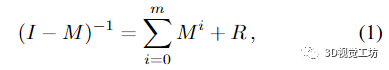
其中误差矩阵

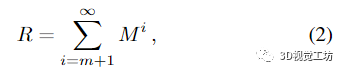
满足

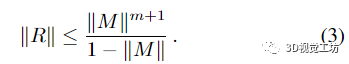
附录给出了证明，图5给出了实际问题的说明

4、power BA

我们考虑具有 np 个位姿和 nl 个地标的BA的一般形式。令 x = （xp， xl） 为包含所有优化变量的状态向量，其中长度为 dp*np 的向量 xp 与所有姿势的外部和（可能）内部相机参数相关联，长度为 3*nl 的向量 xl 与所有地标的 3D 坐标。如果只有外部参数未知，则 dp = 6 用于每个摄像机的旋转和平移。对于评估的 BAL 问题，我们另外估计内在参数和 dp = 9。目标是最小化总BA能量

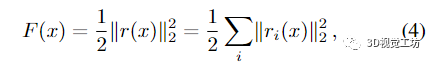
其中向量 r（x） = ［r1（x）， 。..， rk（x）］ 包含捕获模型和观察之间差异的所有残差。

4.1.最小二乘问题

这种非线性最小二乘问题通常使用 Levenberg-Marquardt （LM） 算法求解，该算法基于当前状态估计值 x0 = （x0 p， x0 l ） 的一阶泰勒近似 r（x）。通过添加正则化项来提高收敛性，最小化变成

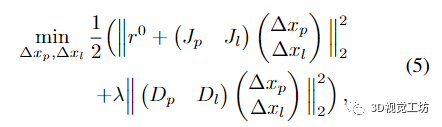
其中

λ 是阻尼系数，Dp 和 Dc 是位姿和地标变量的对角阻尼矩阵。这个阻尼问题导致相应的正规方程

这里

Uλ、Vλ 和 H 是对称正定的 ［16］

4.2.舒尔补

由于直接反演大小为（dpnp+3nl）2的系统矩阵H对于大规模问题往往代价过高，因此通常使用Schur补码技巧进行约简。其想法是形成约简相机系统

同时

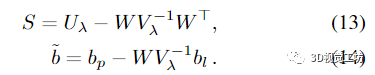
然后求解 （12） 的 Δxp。最优的 Δxl 是通过回代获得的

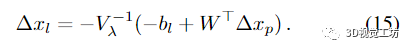
4.3.power BA

用分块矩阵 Uλ 对 （13） 进行因式分解

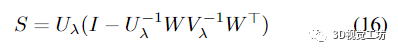
导致将逆 Schur 补表示为

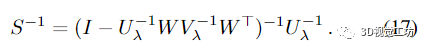
为了将 （17） 展开为命题 1 中详述的幂级数，我们需要将的光谱半径限制为 1

通过利用 BA 问题的特殊结构，我们证明了一个更强大的结果：

引理 1. 令 μ 为的特征值。然后

证明： 一方面， 是对称正半定的，因为 Uλ 和 Vλ 是对称正定的。则其特征值大于 0。由于 与 》 相似，

另一方面， 与 S 和 Uλ 一样是对称正定的。因此，由于 的相似性，U −1 λ S 的特征值都严格为正。作为

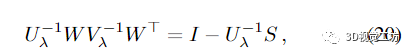
它遵循

证明结束。

假设

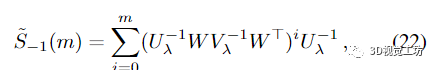
并且

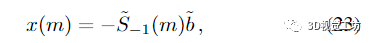
对于 m ≥ 0。以下命题证实了近似值确实随着 m 的递增阶数收敛：

命题2

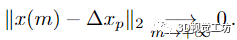
证明。我们表示 P = 。由于引理 1

与 （6） 关联的逆 Schur 补允许幂级数展开：

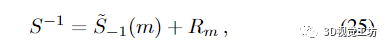
这里

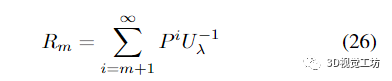
满足

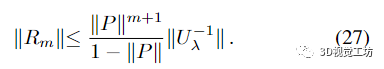
由此得出

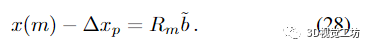
谱范数相对于矢量范数的一致性意味着：

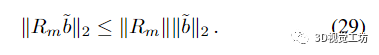
从（24）、（27）和（29）我们得出证明

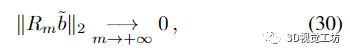
所以

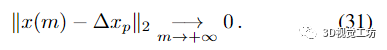
该收敛结果证明：

• 将（22） 应用于（12） 的右侧可以直接获得Δxp 的近似值；

• 这种近似的质量取决于阶数 m 并且可以根据需要尽可能小

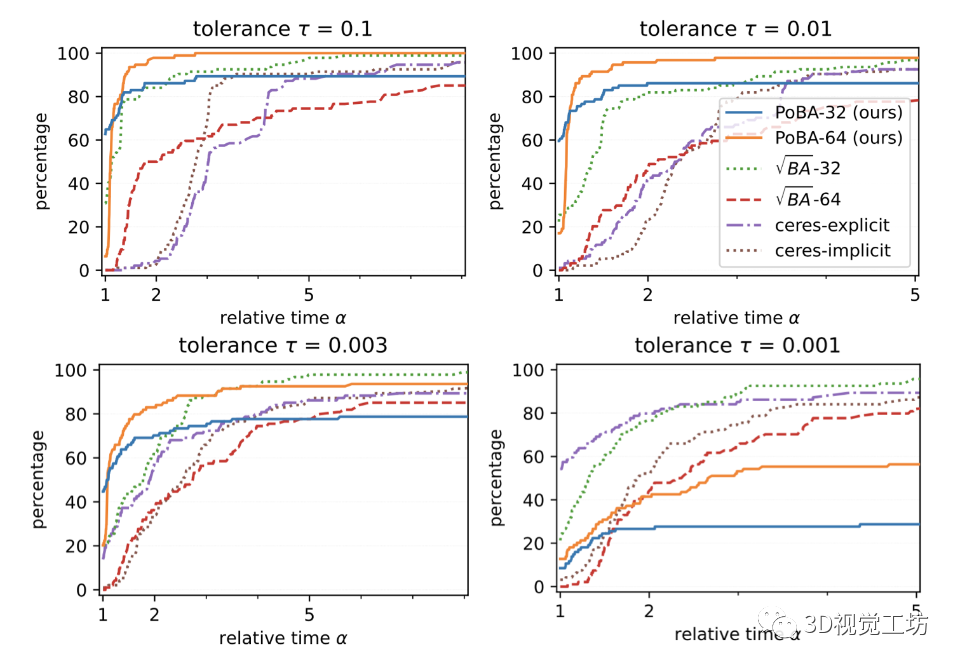
图 3. 所有 BAL 问题的性能概况显示解决给定精度公差 τ ∈ {0.1， 0.01， 0.003， 0.001} 和相对运行时间 α 的问题的百分比。我们提出的求解器 PoBA 使用 Schur 补数的级数展开显着优于所有竞争求解器，精度可达 τ = 0.003。

幂级数展开是迭代导出的，需要终止规则。

通过类比不精确的牛顿法 ［11， 12， 18］ 这样共轭梯度算法我们设置了一个停止标准

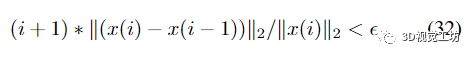
对于给定的。该标准确保当通过将逆 Schur 补码扩展为补充顺序来更新位姿的细化时，幂级数扩展停止

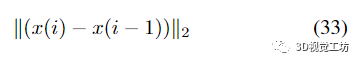
达到同阶时远小于平均细化

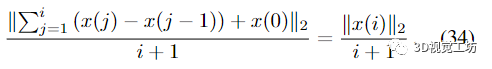
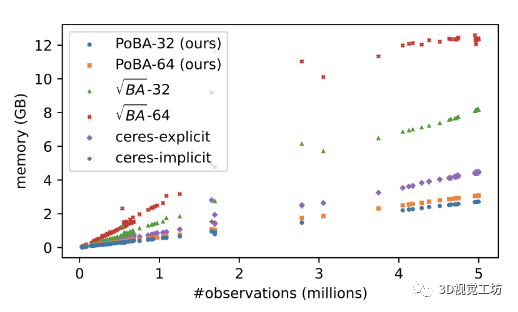
图 4. 所有 BAL 问题的内存消耗。所提出的 PoBA 求解器（橙色和蓝色点）的内存消耗比 √BA 求解器少五倍

5、实现

我们直接在 ［4］ 的公开可用实现 1 上以单 （PoBA-32） 和双 （PoBA-64） 浮点精度在 C++ 中实现我们的 PoBA 求解器。这个最近的求解器通过使用具有里程碑意义的雅可比行列式的 QR 因式分解，表现出出色的性能来解决boundle adjustment。它尤其与流行的 Ceres 求解器竞争。我们还添加了与 Ceres 的稀疏 Schur 补码求解器的比较，类似于 ［4］。Ceres-explicit 和 Ceres-implicit 使用由 Schur-Jacobi 预调节器预处理的共轭梯度算法迭代求解 （12）。第一个将 S 作为块稀疏矩阵保存在内存中，第二个在迭代期间即时计算 S。√BA 和 Ceres 提供了非常有竞争力的性能来解决boundle adjustment问题，这使得它们与 PoBA 相比非常具有挑战性的基线。我们在 MacOS 11.2 上运行实验，配备 Intel Core i5 和 4 个内核，频率为 2GHz。

高效存储

我们利用 BA 问题的特殊结构并设计了内存高效存储。我们按地标对雅可比矩阵和残差进行分组，并将它们存储在单独的密集内存块中。对于具有 k 个观察值的地标，所有与观察到地标的姿势相对应的大小为 2 × dp 的雅可比位姿块被堆叠并存储在大小为 2k × dp 的内存块中。连同大小为 2k × 3 的地标雅可比块和长度为 2k 的残差也与地标相关联，单个地标的所有信息都有效地存储在大小为 2k × （dp + 4） 的内存块中。此外，（15）和（23）中涉及的操作使用内存块并行化。

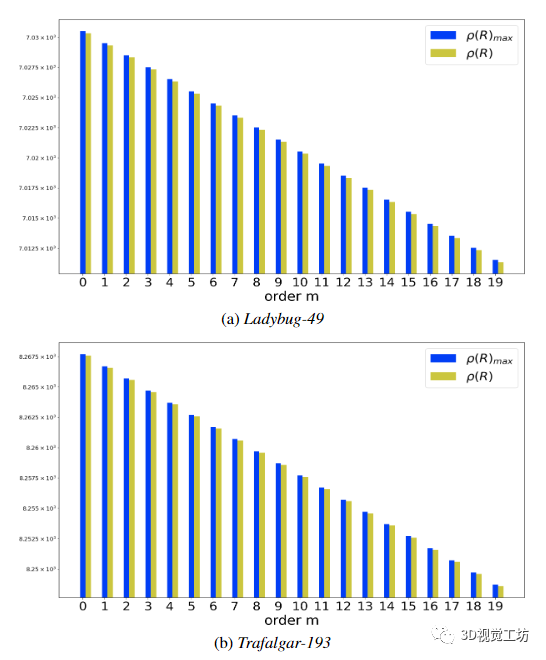
图 5. 两个 BAL 问题的第一次 LM 迭代的命题 1 中的不等式 （3） 的图示：（a） 具有 49 个姿势的瓢虫和 （b） 具有 193 个姿势的特拉法加。当 m 《 20 时，误差矩阵 R 的谱范数以绿色绘制。以蓝色绘制的不等式右侧表示误差矩阵谱范数的理论上限，并且取决于所考虑的 m 和谱M 的范数 = U −1 λ W V −1 λ W 》。对于光谱库 ［23］，ρ（M） 取值 （a） L-49 的 0.999858 和 （b） T-193 的 0.999879。两个值都小于 1，并且 ρ（R） 始终小于 ρ（M ）m+1/（1 − ρ（M ）），如引理 1 中所述。

性能概况

为了比较一组求解器，用户可能对两个因素感兴趣，即运行时间更短和精度更高。性能配置文件 ［6］ 对两者进行联合评估。设 S 和 P 分别是一组求解器和一组问题。令 f0（p） 为初始目标，f （p， s） 为求解器 s ∈ S 在求解问题 p ∈ P 时达到的最终目标。S 中求解器针对问题 p 达到的最小目标是 f ∗（p） = mins∈S f （p， s）。给定公差 τ ∈ （0， 1），问题 p 的目标阈值由下式给出

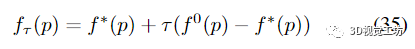
求解器达到这个阈值所需的运行时间被记录为T√（p， s）。很明显，对于给定问题p，最有效的求解器s*达到阈值时，运行时T运行时T会用（p， s*）=min 2 2 S T会用（p， s）。然后，相对运行时α的求解器的性能文件被定义为

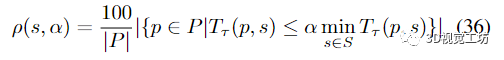
在图形上，给定求解器的性能概况是解决问题的百分比快于 x 轴上的相对运行时间 α

5.1.实验设置

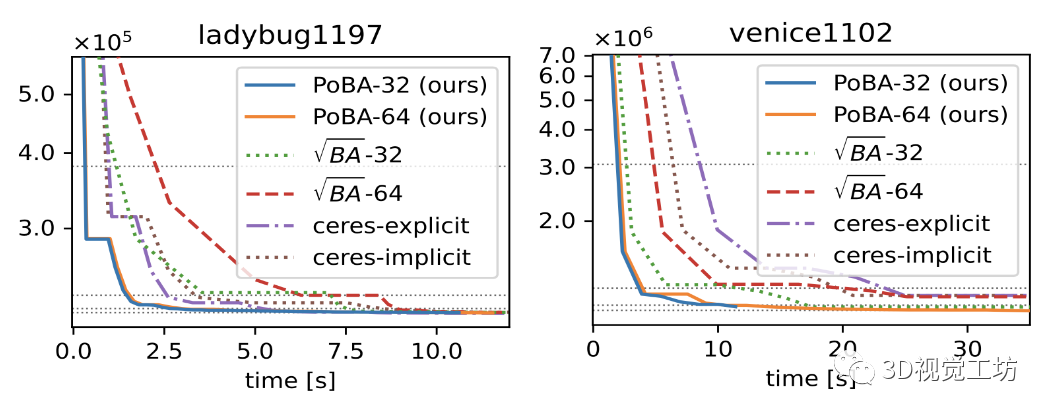
图 6. 来自具有 1197 个姿势的 BAL 数据集的 Ladybug-1197（左）和来自具有 1102 个姿势的 BAL 数据集的 Venice-1102（右）的收敛图。图 1 显示了针对这些问题的 3D 地标和相机姿势的可视化。虚线对应于公差 τ ∈ {0.1， 0.01， 0.003， 0.001} 的成本阈值

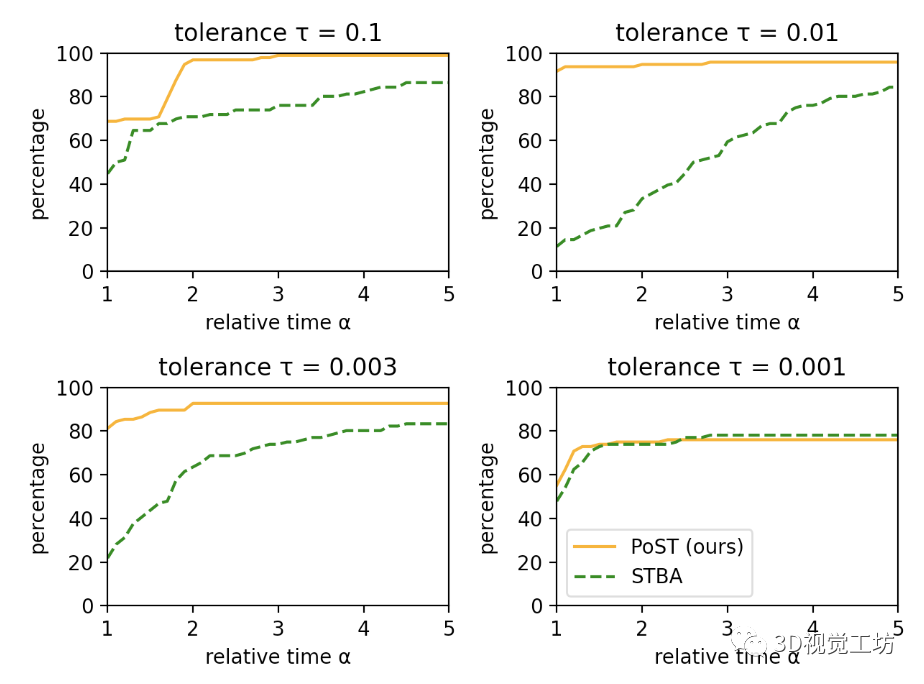
图 7. 使用随机框架的所有 BAL 问题的性能概况。我们提出的求解器 PoST 在所有精度公差 τ ∈ {0.1， 0.01， 0.003} 方面都优于具有挑战性的 STBA，无论是在速度还是精度方面，并且在 τ = 0.001 时与 STBA 相媲美

数据集

为了进行广泛的评估，我们使用了BAL项目页面上的所有97个boundle adjustment问题。它们被分成五个问题家族。瓢虫是由以正常速度行驶的车辆拍摄的图像组成的。威尼斯、特拉法尔加和杜布罗夫尼克的图像来自Flickr.com，并被保存为骨骼集［1］。用额外的树叶图像重组这些问题导致了菲纳尔家族。关于这些问题的详细信息可以在附录中找到

LM循环

PoBA 符合实施 ［4］ 和 Ceres。从阻尼参数 10−4 开始，我们根据 LM 循环的成功或失败更新 λ。我们将 LM 迭代的最大次数设置为 50，如果达到 10−6 的相对函数公差，则提前终止。关于（23）和（32），我们将最大内部迭代次数设置为 20，阈值 = 0.01。Ceres 和√BA 对内部 CG 循环使用相同的强制序列，其中最大迭代次数设置为 500。

5.2.分析

图 3 显示了具有公差 τ ∈ {0.1， 0.01， 0.003， 0.001} 的所有 BAL 数据集的性能概况。对于 τ = 0.1 和 τ = 0.01，PoBA-64 在运行时间和准确性方面明显优于所有挑战者。在高相对时间 α = 4 之前，PoBA-64 显然仍然是出色精度 τ = 0.003 的最佳求解器。对于更高的相对时间，它与 √BA − 32 具有竞争力，并且仍然优于所有其他挑战者。从两个不同大小的 BAL 问题的收敛图中可以得出相同的结论（见图 6）。图 4 突出显示了 PoBA 相对于所有 BAL 问题的挑战者的低内存消耗。无论问题的大小如何，PoBA 的内存消耗都比√BA 和 Ceres 少得多。值得注意的是，它需要的内存比√BA 少近五倍，比 Ceres-implicit 和 Ceres-explicit 少几乎两倍的内存

5.3.power 随机BA （PoST）

随机BA。

STBA 将简化的相机系统分解为 Levenberg-Marquardt 迭代内的集群。由于相机集群内部的密集连接，每个集群的线性子问题然后与密集 LL》 分解并行解决。如 ［22］ 所示，这种方法在运行时和扩展到非常大的 BA 问题方面优于基线，它甚至可以用于分布式优化。在下文中，我们展示了用我们的 Power Bundle Adjustment 替换子问题求解器可以进一步显著提高运行时间

power 随机BA （PoST）

我们通过结合我们的求解器而不是密集的 LL》 分解来扩展 STBA2。然后使用与第 5.1 节中相同的参数对逆 Schur 补码进行幂级数展开来求解每个子问题。根据 ［22］，我们将最大簇大小设置为 100，并在 C++ 中用 double 编写实现

分析

图 7 显示了针对不同公差 τ 的所有 BAL 问题的性能配置文件。对于 τ = 0.001，两种求解器都具有相似的精度。对于 τ ∈ {0.1， 0.01， 0.003}，PoST 在运行时间和准确性方面明显优于 STBA，尤其是 τ = 0.01。当我们绘制不同大小的 BAL 问题的收敛曲线时，会进行相同的观察（见图 8）

六，结论

我们引入了一类新的大规模BA求解器，它利用逆 Schur 补码的幂展开。我们证明了所提出的近似的理论有效性和该求解器的收敛性。此外，我们通过实验证实，所提出的逆 Schur 补数的幂级数表示在速度、准确性和内存消耗方面优于竞争迭代求解器。最后但同样重要的是，我们证明了幂级数表示可以补充分布式BA方法，以显着提高其在大规模 3D 重建中的性能。

审核编辑 ：李倩