如何使用LTspice对复杂电路的统计容差分析进行建模

LTspice可用于对复杂电路进行统计容差分析。本文将介绍使用蒙特卡罗和高斯分布进行公差分析的技术，以及LTspice中的最坏情况分析。为了显示该方法的有效性，在LTspice中模拟了一个电压调节示例电路，演示了内部基准电压源和反馈电阻的蒙特卡罗和高斯分布技术。将此仿真的结果与最坏情况分析仿真进行比较。包括四个附录。附录A提供了有关调整后基准电压源分布的见解。附录B提供了LTspice中高斯分布的分析。附录C提供了由LTspice定义的蒙特卡罗分布的图形视图。附录D提供了编辑LTspice原理图和提取仿真数据的说明。

本文说明了可以使用LTspice完成的统计分析。这

公差分析

在系统设计中，必须考虑参数公差约束，以确保设计成功。一种常见的方法是使用最坏情况分析 （WCA），其中所有参数都调整到其最大公差限值。在最坏情况分析中，分析系统性能以确定最坏情况结果是否在系统设计规范范围内。WCA的功效存在局限性，例如：

WCA要求确定哪些参数必须最大化或最小化才能获得真正的最坏情况结果。

WCA结果通常违反设计规范要求，导致选择昂贵的组件以获得可接受的结果。

WCA结果在统计上并不代表通常观察到的结果;要观察表现出WCA性能的系统可能需要大量组装系统。

系统公差分析的另一种方法是使用统计工具进行组件公差分析。统计分析的好处是，结果数据具有反映物理系统中通常应测量的内容的分布。在本文中，LTspice用于仿真电路性能，将蒙特卡罗分布和高斯分布应用于参数容差变化。这与WCA模拟进行了比较。

尽管WCA存在明显的问题，但最坏情况和统计分析都为系统设计提供了宝贵的见解。有关使用LTspice应用WCA的非常有用的教程，请参阅Gabino Alonso和Joseph Spencer的“LTspice：最小仿真运行的最坏情况电路分析”。

蒙特卡洛分销

图1显示了在LTspice中建模的具有蒙特卡罗分布的基准电压源。电压源标称值为1.25 V，容差为1.5%。蒙特卡罗分布定义了 1.5% 容差范围内的 251 种电压状态。图 2 显示了 50 个箱的 251 个值的直方图。表 1 说明了分布的相关统计信息。

图1.具有蒙特卡罗分布的电压源的LTspice原理图。

图2.蒙特卡罗仿真结果为 1.25 V 基准电压源、50 个箱、251 个点的直方图。

 

	结果
平均	1.249933
最低	1.2313
最大	1.26874
标准差	0.010615
错误正	1.014992
负误差	0.98504

 

正态分布

图3显示了在LTspice中建模的具有高斯分布的基准电压源。电压源标称值为1.25 V，容差为1.5%。蒙特卡罗分布定义了 1.5% 容差范围内的 251 种电压状态。图 4 显示了包含 50 个箱的 251 个值的直方图。表 2 说明了分布的相关统计信息。

图3.具有3西格玛高斯分布的电压源的LTspice原理图。

图4.3-sigma 高斯仿真结果为 1.25 V 基准电压源、50 个箱、251 个点的直方图。

 

	结果
最低	1.22957
最大	1.26607
平均	1.25021
标准差	0.006215
错误正	1.012856
负误差	0.983656

 

高斯分布是具有钟形曲线和概率密度的正态分布，如图 5 所示。

图5.正态 3 西格玛高斯分布。

理想分布和LTspice模拟高斯分布之间的相关性如表3所示。

 

	模拟	理想
1-西格玛点差	67.73%	68.27%
2-西格玛点差	95.62%	95.45%
3-西格玛传播	99.60%	99.73%

 

为了总结上述仿真，LTspice可用于仿真电压源的高斯或蒙特卡罗容差分布。该电压源可用于对DC-DC转换器中的基准电压源进行建模。LTspice高斯分布仿真与预测的概率密度分布非常匹配。

DC-DC转换器仿真的容差分析

图6是DC-DC转换器的LTspice仿真原理图，该转换器使用电压控制电压源对闭环电压反馈进行建模。反馈电阻R2和R3的标称值为16.4 kΩ和10 kΩ。基准电压源标称值为1.25 V。本电路中，标称稳压，V外或设定值为 3.3 V。

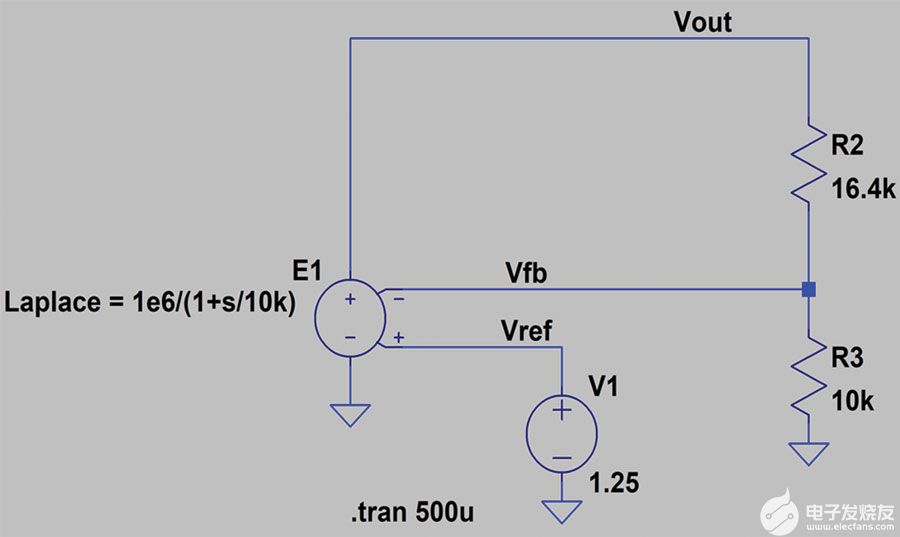
图6.LTspice DC-DC转换器仿真原理图。

为了模拟电压调节的容差分析，反馈电阻R2和R3的容差定义为1%，内部基准电压源的容差定义为1.5%。本节将介绍三种公差分析方法：使用蒙特卡罗分布的统计分析、使用高斯分布的统计分析和最坏情况分析 （WCA）。

图7和图8显示了使用蒙特卡罗分布进行仿真的原理图和电压调节直方图。

图7.使用蒙特卡罗分布进行公差分析的示意图。

图8.使用模拟蒙特卡罗分布的电压调节直方图。

图9和图10显示了使用高斯分布进行仿真的原理图和电压调节直方图。

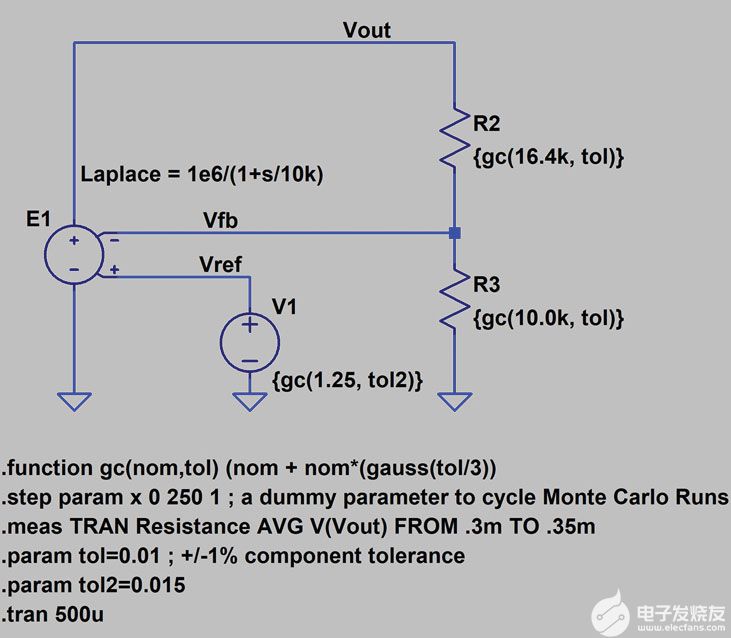
图9.使用高斯分布进行公差分析的示意图。

图 10.使用模拟高斯分布进行公差分析的直方图。

图11和图12显示了使用WCA进行仿真的原理图和电压调节直方图。

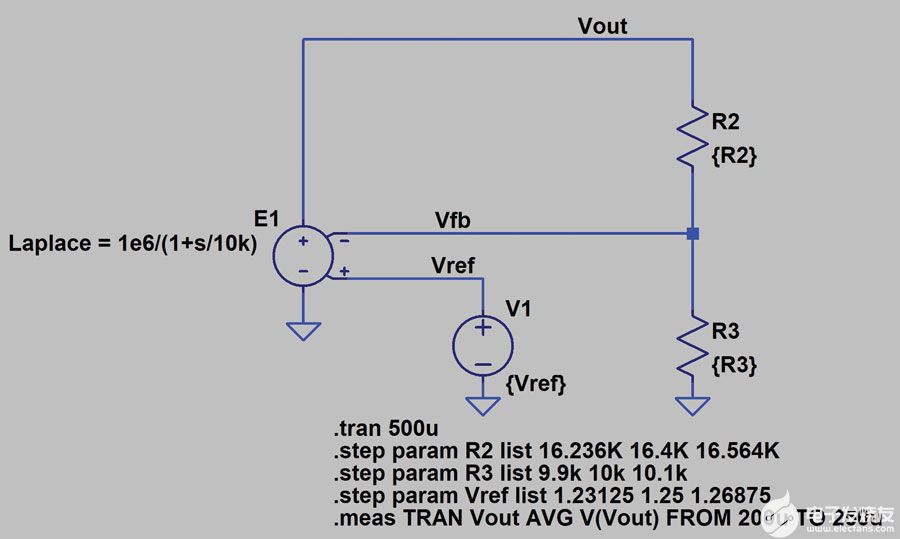
图 11.使用模拟WCA进行公差分析的原理图。

图 12.使用 WCA 进行公差分析的直方图。

表4和图13比较了公差分析结果。在此示例中，WCA 预测最大最大偏差，基于高斯分布的模拟预测最小偏差。图 13 中的盒状和晶须图对此进行了说明——实心框表示 1 西格玛极限，而晶须表示最小值和最大值。

 

	世界卫生协会	高斯	蒙特卡洛
平均	3.30013	3.29944	3.29844
最低	3.21051	3.24899	3.21955
最大	3.39153	3.35720	3.36922
标准差	0.04684	0.01931	0.03293
错误正	1.02774	1.01733	1.02098
错误正	0.97288	0.98454	0.97562

 

图 13.调节电压分布的盒须图形比较。

总结

使用简化的DC-DC转换器模型，分析了三个变量，两个反馈电阻和内部基准电压源用于对电压设定点调节进行建模。使用统计分析，给出了最终的电压设定点分布。结果以图形方式绘制。这与最坏情况的计算相比。由此产生的数据表明，最坏情况限制在统计上是不可能的。