

Workbench结构分析中常见的概念和易错问题
电子说
描述
导读:随着Ansys的不断迭代更新,Mechanical继续提供可实现快速仿真,更简易工作流程和具有记录功能脚本等功能,并具备增强求解器功能的产品集成能力。由此可见,软件工具正在降低学习门槛,而且功能越来越强大,不少用户乐此不疲,但是对软件背后的有限元理论和工程结构应用概念的学习却令人堪忧!
一、不知道的重要概念
在ANSYS结构分析中,有限元模型的每个节点都有一个叫做节点坐标系的固有属性,并可以根据需要将节点坐标系转换至需要的任意局部坐标方向。那么为什么相当多的Workbench结构分析用户没听说过这个概念呢?
这可能是因为在Mechanical组件中进行前处理时经常采用基于几何对象的直观操作,几乎不直接涉及到有限元模型。直到在比较新的ANSYS版本中,Mechanical组件中才新增了针对有限元模型的操作。
那么在什么情况下需要用到节点坐标系呢?来看下面的三个问题。
1、第一个问题如下图所示,梁的右端节点需要施加135度方向的倾斜支座以及45度方向的力。
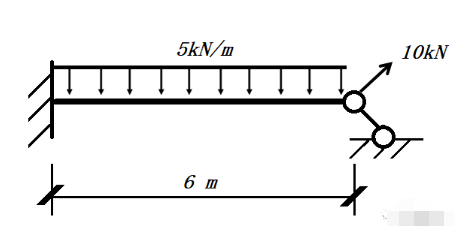
对于这个问题,可以通过Mechanical组件中的Nodal Orientation来实现。
首先定义一个相对总体坐标绕Z轴旋转45度的局部坐标系,如上图所示。然后把右端节点坐标系定位到局部坐标系。这样,对于右端节点,45度和135度方向分别对应X和Y方向,然后施加Y方向节点位移和X方向节点力即可。
2、再来看第二个问题,在Mechanical组件中有一个Cylindrical约束,可以约束圆柱面的径向、轴向以及切向的任意一个、两个或三个方向,如下图所示。
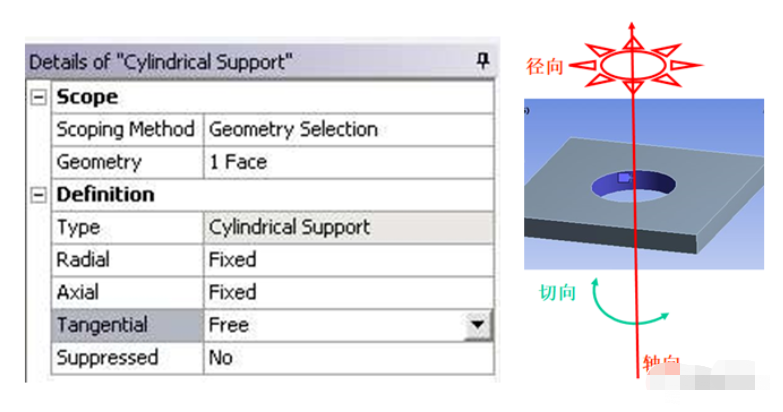
这个Cylindrical约束表面上是针对圆柱面的,但在实际上,ANSYS内自动定义了局部的柱坐标系,并且把圆柱面的节点都转换到了圆柱坐标系方向。此外,施加于圆柱面的Frictionless Support也涉及到约束圆柱面任意一点的径向,内部实际上也涉及到了节点坐标转换的问题。
3、在Cylindrical Support的基础之上,我们再来看第三个问题。
Cylindrical Support可以对圆柱面施加局部坐标方向的约束了,但如果需要施加非零位移,比如在圆柱面上施加一个径向的位移,那么就无法直接引用Cylindrical Support,而需要用户自行定义并转换节点坐标系。
如下图所示为一个圆筒,内、外直径分别为0.8m和1.0m,轴向长度2.0m,外表面施加一个径向的压缩位移5mm,这如何来操作呢?

实现的方法如下:
第一步,建立一个与圆柱体同轴的局部的圆柱坐标系。
第二步,选择外表面形成Named Selection。
第三步,添加新的Named Selection并选择Worksheet方式,通过Convert方法将表面集合转换为节点集合。
第四步,对外表面节点组成的Named Selection施加Nodal Orientation,转换节点坐标至第一步定义的局部柱坐标系。
第五步,对外表面节点Named Selection施加Nodal Displacement,并在X方向上指定具体的位移约束即可。
当然,计算之前还需指定其他的约束,比如内表面施加径向位移为0的圆柱面Cylindrical约束,再打开Weak Spring选项,即可计算。
计算完成后,查看Directional Deformation,其Details中选择Coordinate System为局部柱坐标,并选择X方向变形,得到圆筒径向变形如下图所示,图中显示了变形前的轮廓作为比较。
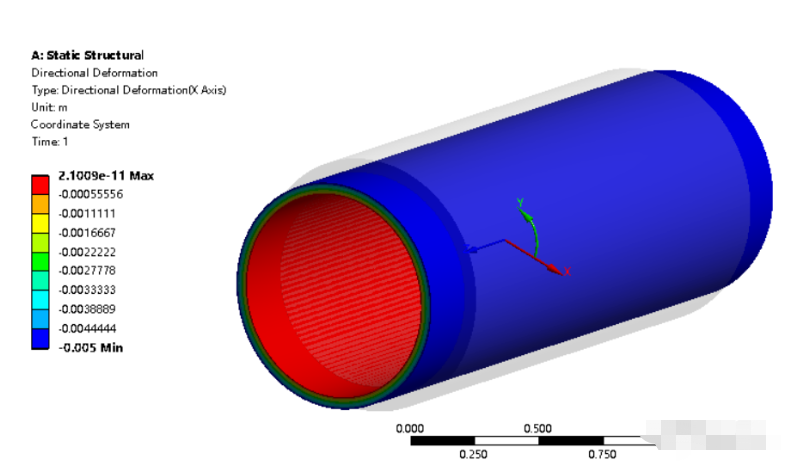
由变形云图可以看出,整个圆柱筒为径向的均匀压缩而轴向均匀伸长的变形状态,表明径向位移得到了正确的施加。
二、一个常见的错误
1、问题的提出
如图所示,1m×1m×10m的实体悬臂杆,沿着长度方向划分为1m×1m×1m尺寸的10个方块单元,左侧面固定。
首先看静力分析,右侧施加一个1000N的横向荷载,此问题的自由端变形根据悬臂梁的理论解答应为2E-5m,采用上述网格计算时会弹出如下的警告信息,随后求解失败,在Output中能看到“small equation solver pivot term”错误信息。
如果进行模态分析,则前6阶频率计算结果几乎均为0,如下图所示为一阶模态及前6阶频率计算结果。
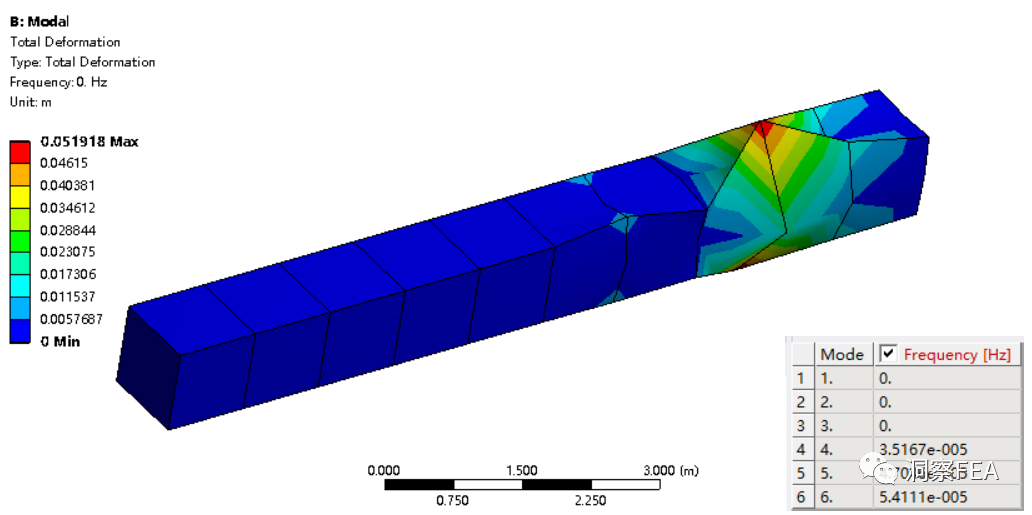
由此可见,厚度方向采用一个实体单元,即便在Workbench中默认采用了二次单元,计算也出现了由于零能模式引起的计算问题。
出现上述问题的原因,是由于采用了SOLID186单元的URI缩减积分算法,如下图所示为Output中的相关信息:

2、第一种解决方案
为了克服零能模式的影响,至少在厚度方向采用两个二次单元,得到如下图所示的网格:
首先进行静力分析,得到梁的最大变形约为2E-5m,与理论值一致。
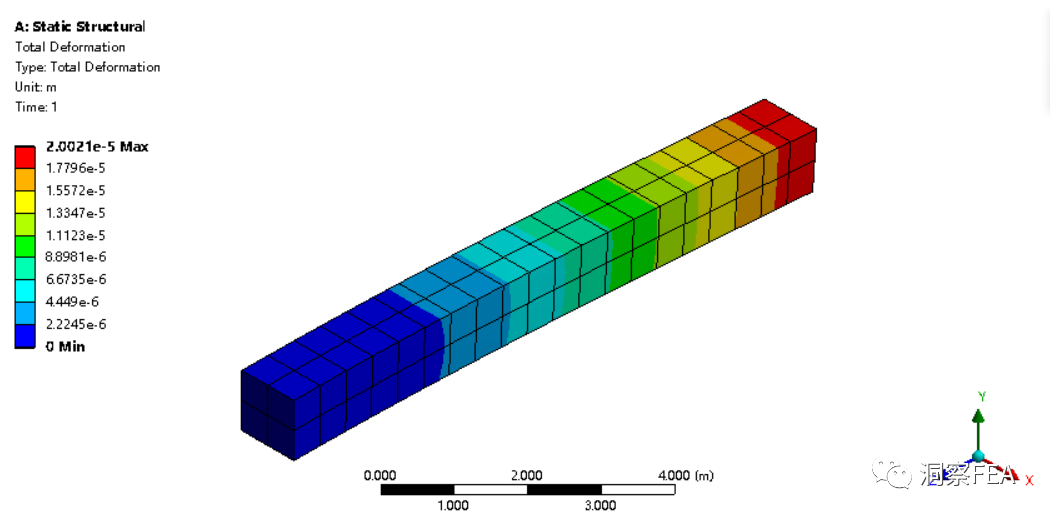
然后进行模态分析,得到梁的一阶振型如下图所示,一阶频率约为8Hz。
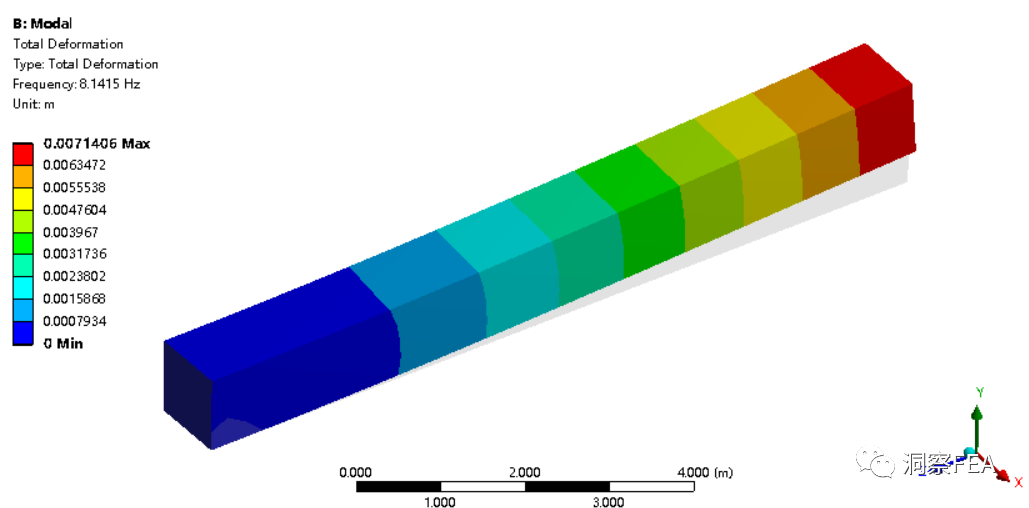
3、第二种解决方案
除了多划分一层单元外,如果仍然采用单层网格,则更换单元算法为全积分也可克服上述计算问题。
如果采用了全积分,且仍然采用单层单元,则静力计算的变形等值线如下图所示,其最大变形为1.979E-5m,与理论解答的误差很小。
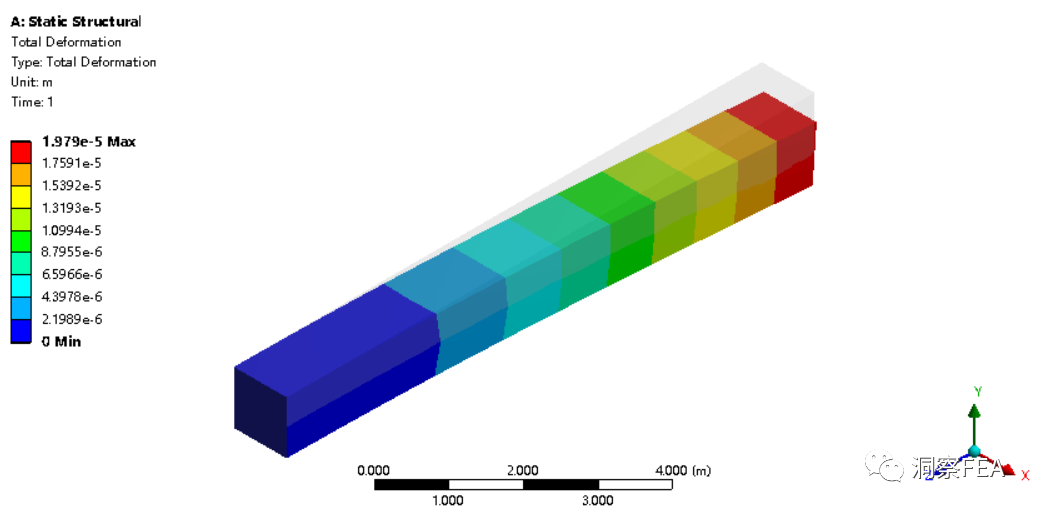
全积分单层单元计算的一阶频率也大约为8Hz,一阶振型如下图所示,计算结果正确。
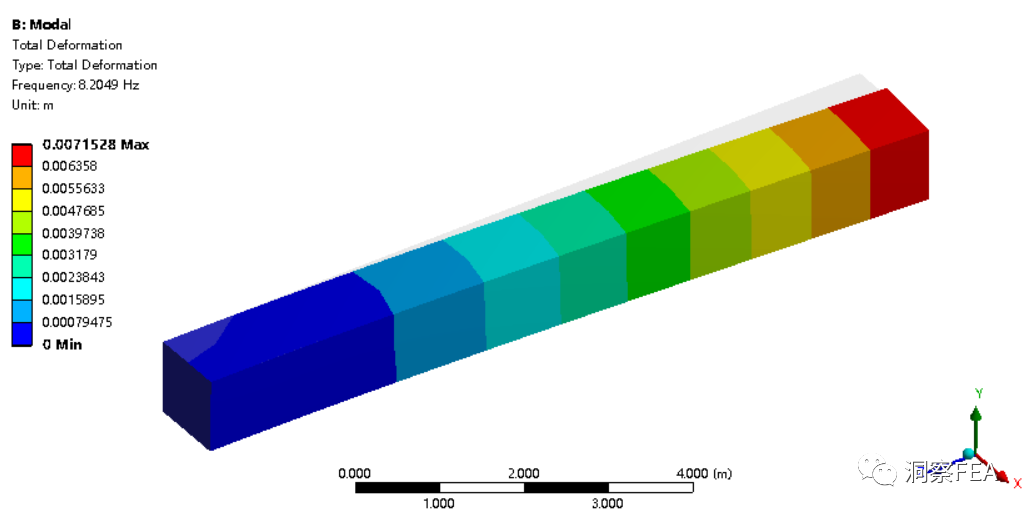
综上所述,
在实体结构分析中要避免厚度方向仅有一层单元的情况,否则将导致不正确的计算结果。
如果在厚度方向上仅一层单元,可通过加密网格或者单层全积分二次单元等方式获取正确解答。
以上是笔者例举的Workbench结构分析中常见的概念和易错问题。其实在Workbench学习与工程结构应用过程中,类似这样的概念和误区还有很多。笔者已多次撰文和公开直播,希望对学习者有些许帮助吧。
编辑:黄飞
- 相关推荐
- 热点推荐
- WORKBENCH
-
FPGACPLD中常见模块设计精华集锦2012-08-17 4142
-
电子书:电源研发过程中常见的问题2019-02-20 5306
-
频谱分析仪在使用过程中常见故障汇总2020-05-20 1678
-
Jackson常用的知识点和易错点2020-06-12 1102
-
电源中常见的故障现象如何维修2021-03-11 1836
-
嵌入式测控系统中常见的数字滤波算法有哪些?2021-04-12 1323
-
HDMI I/O设计和测试中常见的问题?怎么解决?2021-06-02 1650
-
QuartesⅡ时序分析中常见的时间参数有哪些?2021-09-18 1448
-
介绍开发者在ESP8266开发中常见的一些问题2021-11-10 997
-
ANSYS Workbench 疲劳分析培训资料2010-02-24 1012
-
电动车用电池使用中常见问题及原因分析2009-11-11 1094
-
网络设备中常见术语含义及故障分析2011-12-27 15066
-
运放OP闭环电路小信号分析中常见的问题2023-07-14 1332
-
直线导轨使用中常见的问题有哪些2023-08-03 1898
-
理解STM32控制中常见的PID算法2023-10-17 3312
全部0条评论

快来发表一下你的评论吧 !

