PnP几何结构和算法原理详解

PnP(Perspective-n-Point)问题的几何结构如图1所示，给定3D点的坐标、对应2D点坐标以及内参矩阵，求解相机的位姿。

数学语言描述如下：

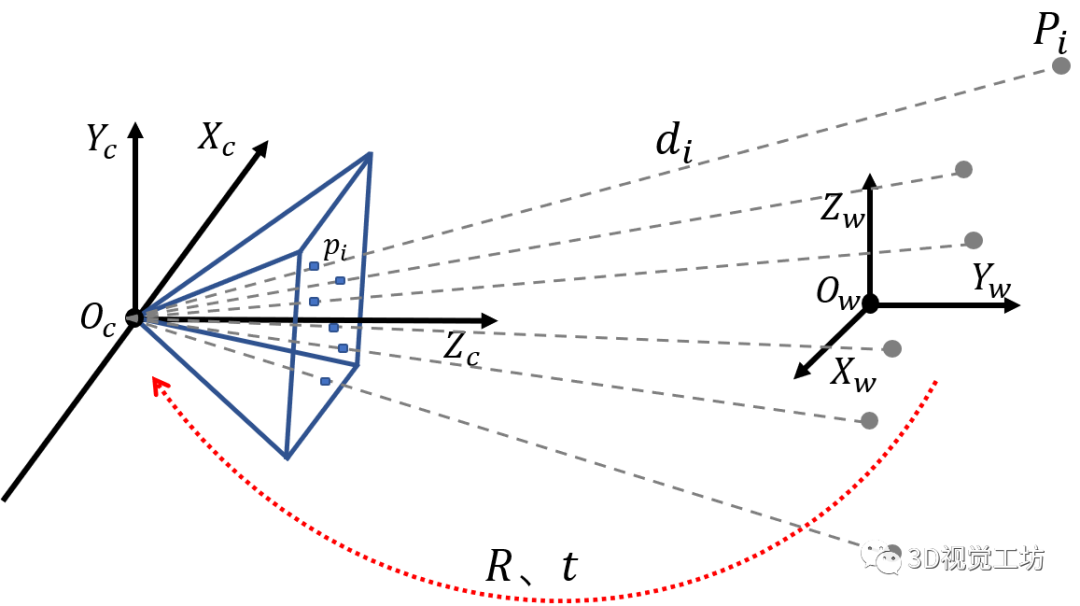
图1.PnP几何结构

1.直接线性变换法(Direct Linear Transform，DLT)

假设：摄像机已经校准过了。 已知：

求解相机的外参：R、t 透视投影模型为：

每组3D-2D匹配点对应两个方程，一共有12个未知数，至少需要6组匹配点。 设有N组匹配点，则：

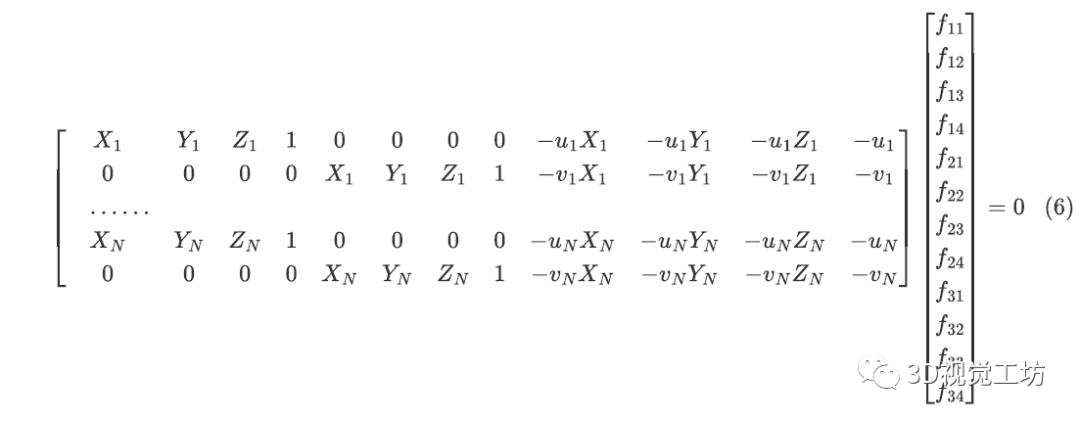
上式写成矩阵形式： AF=0 当N=6时，可以直接求解线性方程组。

因此, 旋转矩阵, 平移矩阵求得:

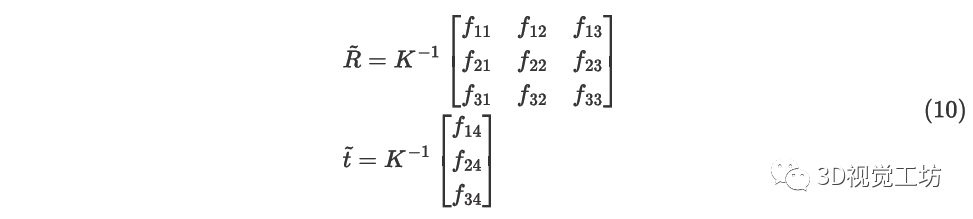
2.P3P

P3P问题是已知三个3D目标点与其2D投影之间的对应关系，来确定标定相机的位姿问题。  

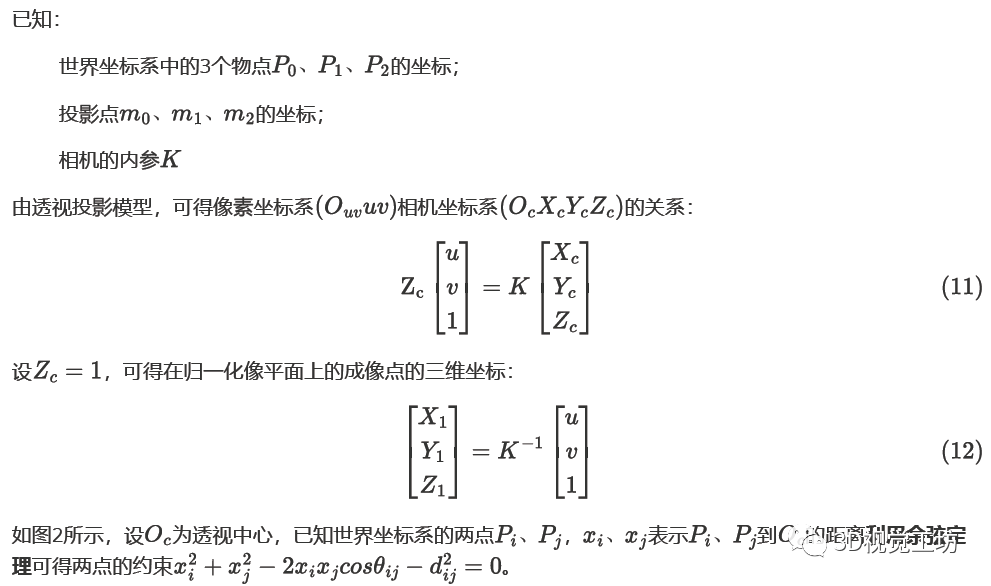
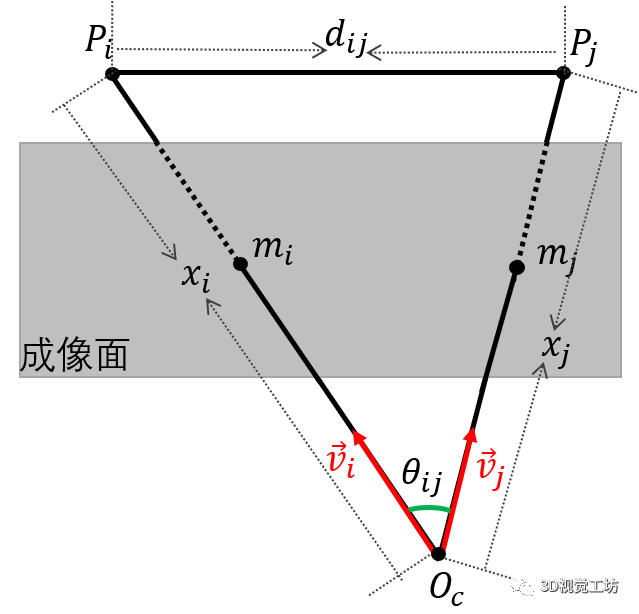
图2.两点约束

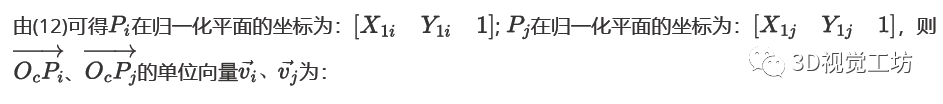
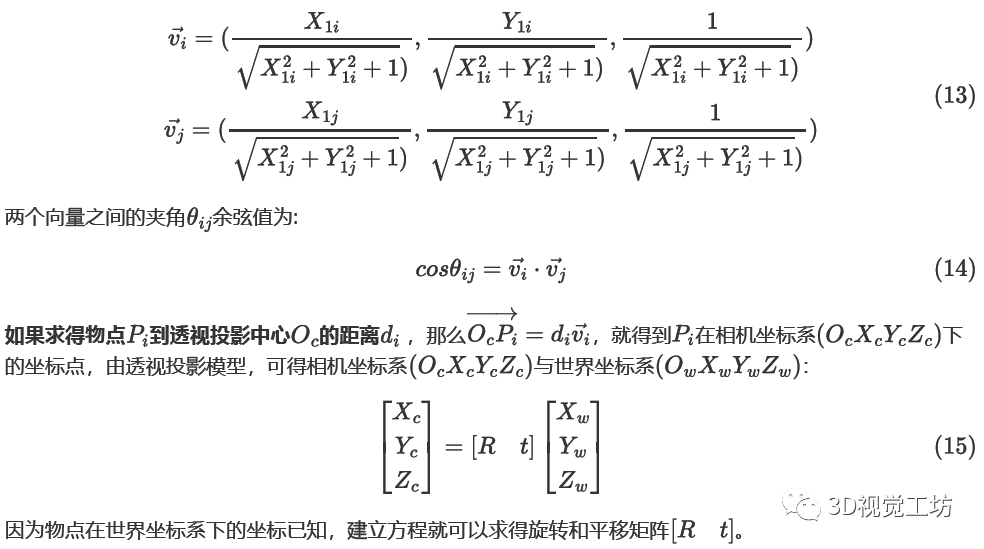
注：直接线性变换法，只考虑了线性意义下的最优解，没有考虑几何约束。而P3P考虑了三角约束，给出三角约束意义下的最优解

2.1 Zero Structure for the P3P Equation System

文章[1]：Complete Solution Classification for the Perspective-Three-Point Problem  

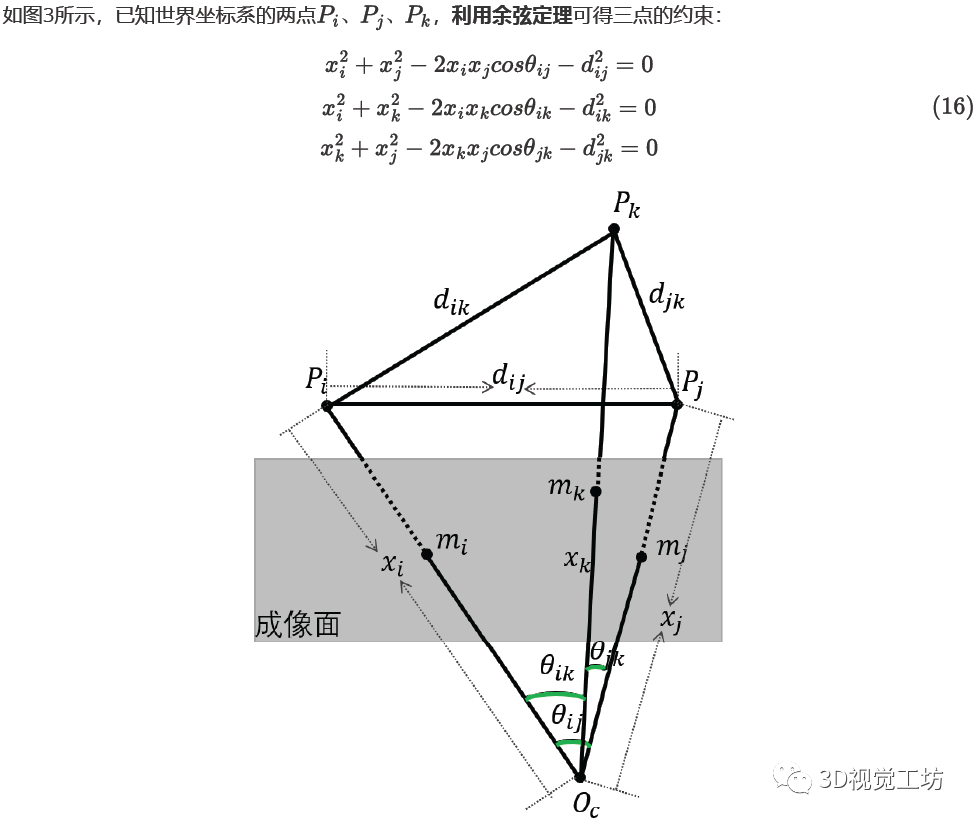
图3.三点约束 对于公式（16）的变量有一些真实的约束：  

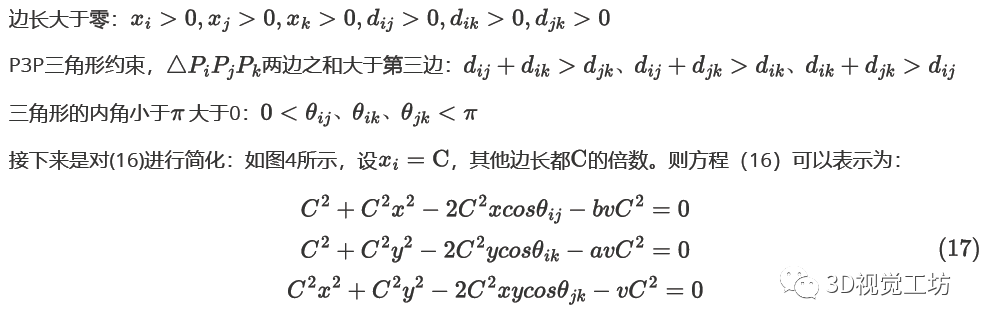
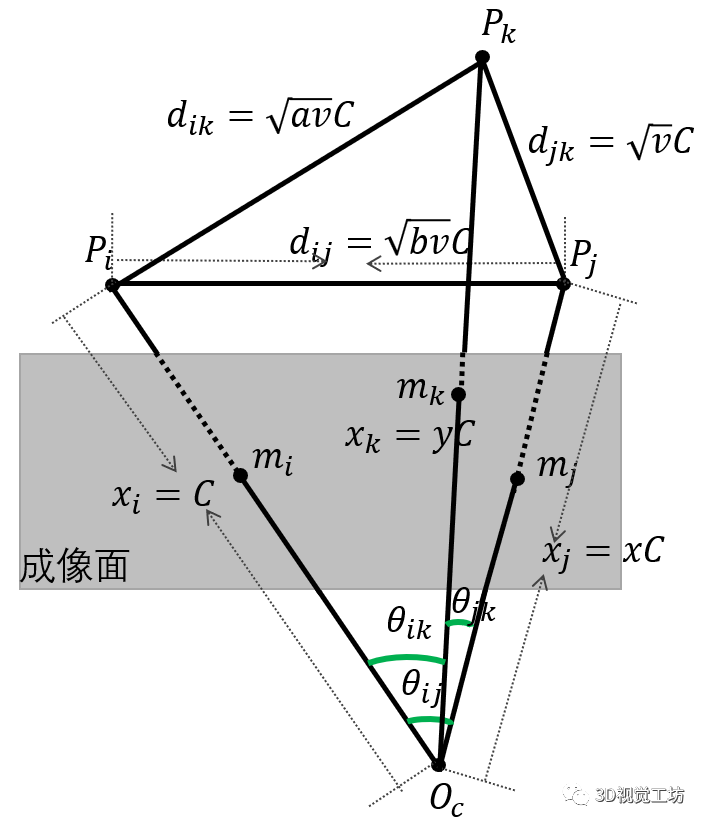
图4.三点约束--重定义边长 公式(17)消去C、v，得ES：  

2.2 PST

文章[2]：A Stable Direct Solution of Perspective-Three-Point Problem 使用相似三角形，利用几何约束来减少未知参数的个数，把P3P方程组转化为四次方程，该称为透视相似三角形方法(Perspective Similar Triangle ，PST)。

（1）P3P问题转为PST问题

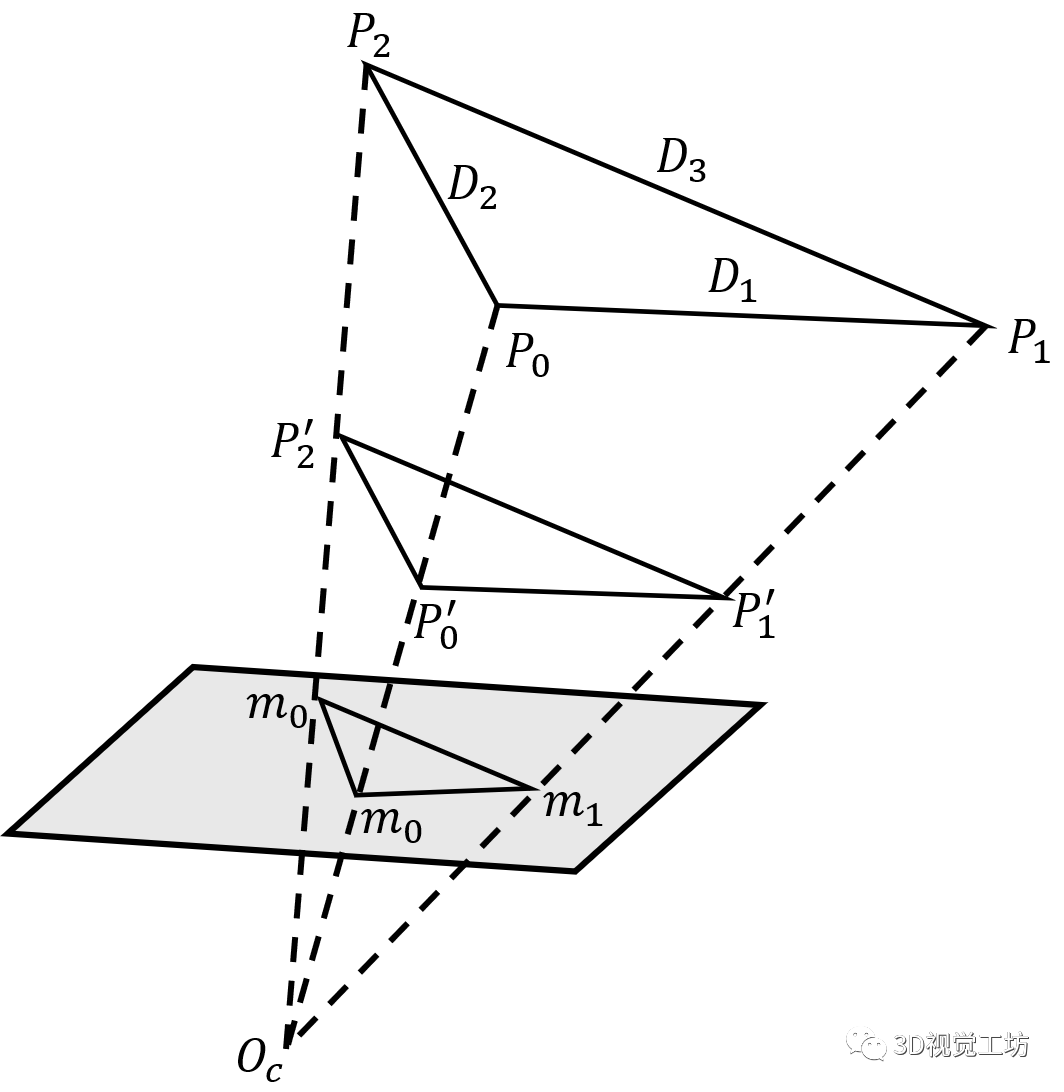
图5.P3P几何结构

（2）PST的求解

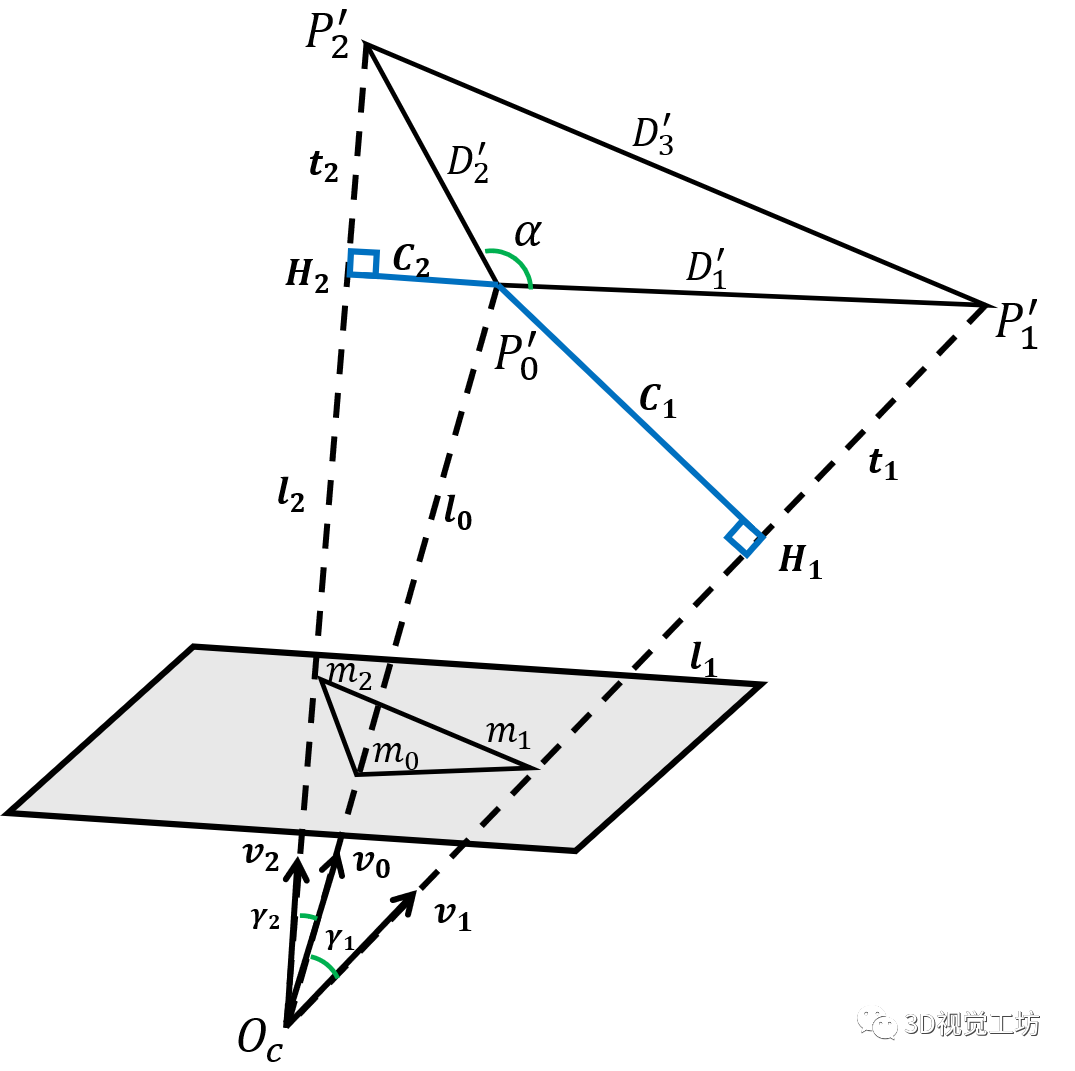
图6.PST几何结构 约束1：相似三角形对应边成比例  

所以：

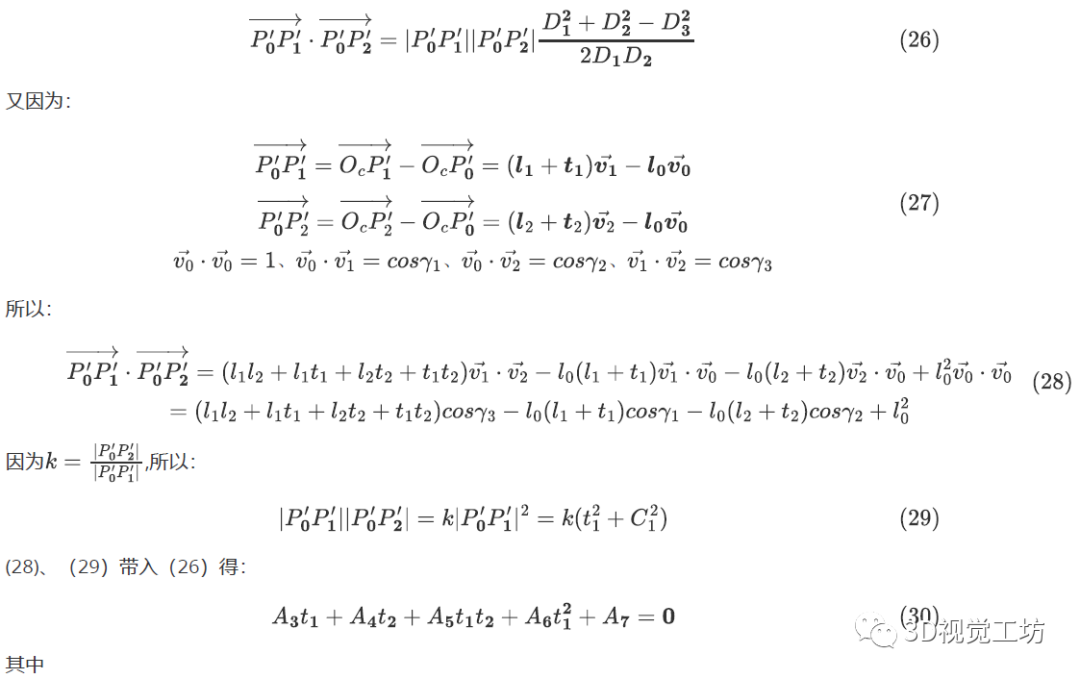
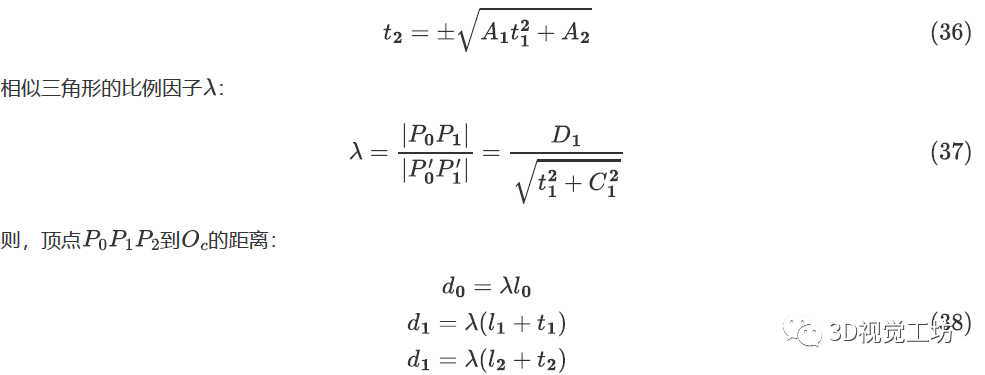
（3）PST多解和缺解问题

由PST(perspective similar Triangle)求解，可得方程组等效转换为四次多项式  

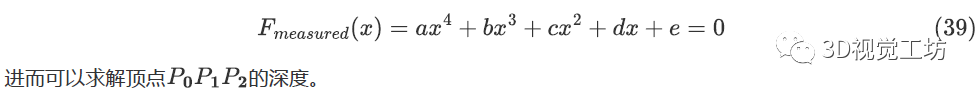
多解问题： 由于存在多组解，相机位姿不能从3点集唯一确定的。解的个数直接对应于四次多项式实根的个数。要得到唯一的解，至少还应引入一点，构建2个三角形，进行求解。另一种方法是RANSAC算法，该算法将点集划分为3个点子集，检查这些子集的一致性。 RANSAC算法参考文献：Random Sample  Consensus: A  Paradigm for Model  Fitting with  Apphcatlons to Image  Analysis and  Automated  Cartography 缺解问题：

缺解问题是由P3P的固有结构决定的，其他P3P方法，如迭代解法、几何解法和分类法，也有同样的问题。

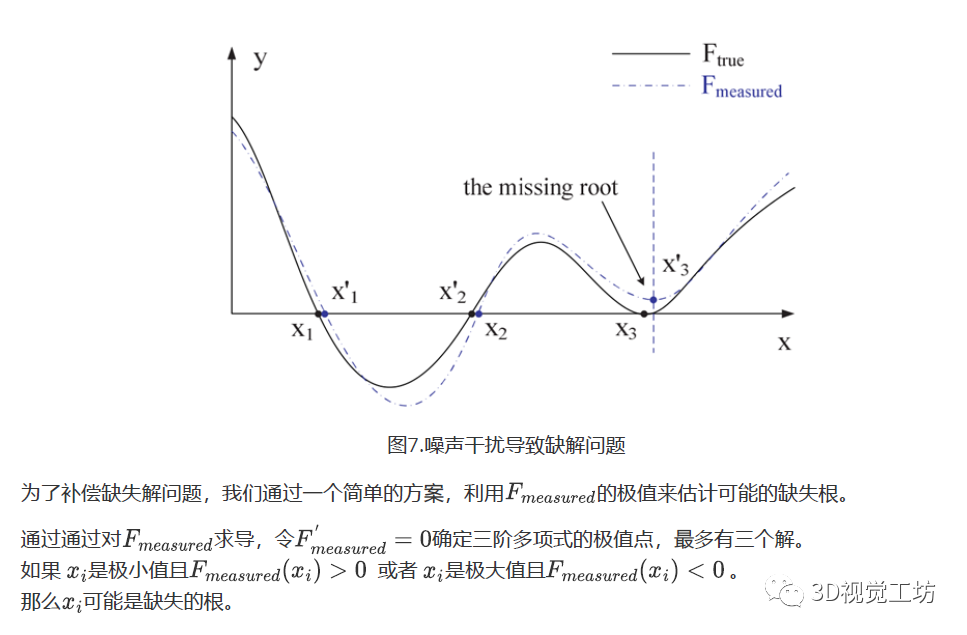
3.RPnP

文章[3]：A Robust O(n) Solution to the Perspective-n-Point Problem  

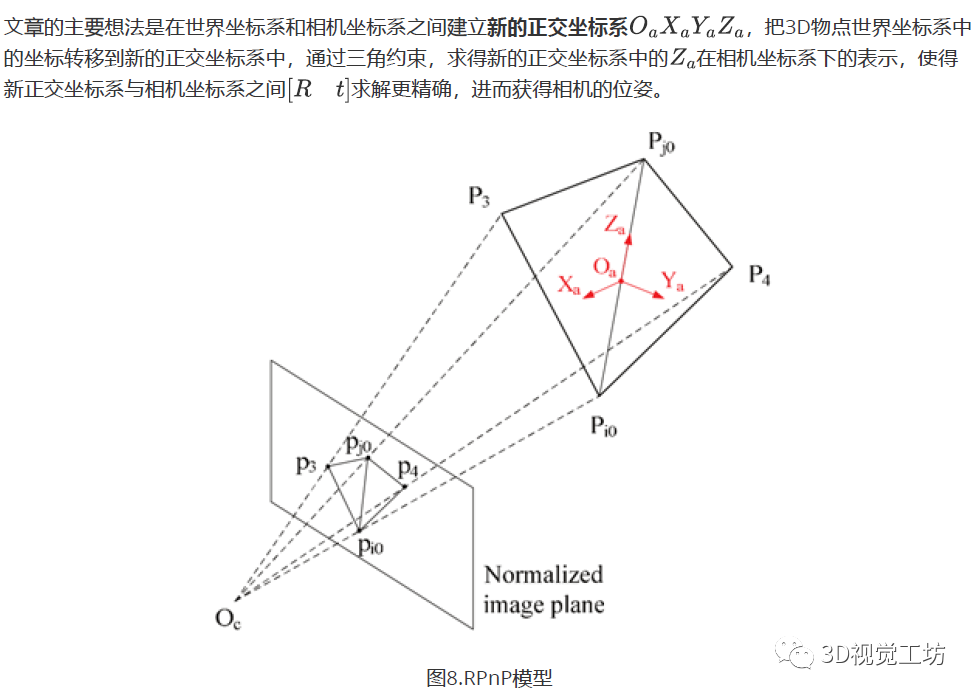
下面来看一下，如何建立新的正交坐标系，以及如何求解正交坐标系到相机坐标系之间[R T]。

3.1确定旋转轴

当确定旋转轴时，只需求解剩余的旋转和三个平移参数，减少了未知变量的数量，来提高方程组的数值精度。

3.2求解旋转角和平移矢量的方程

相机坐标系与新坐标系绕之间的旋转矩阵：

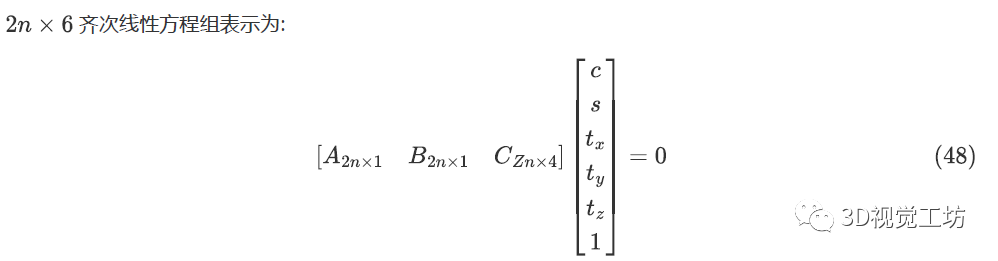
其中,  

3.3获取相机的位姿

再获取到相机坐标系与新坐标系绕之间的旋转和平移矩阵，进而可直接相机坐标系与世界坐标系绕之间旋转和平移矩阵，即相机的位姿。

审核编辑：郭婷