基于IMU和地磁传感器的捷联惯性导航系统

作者：Joel Li 和 Van Yang

本文介绍我们使用ADI公司的惯性测量单元（IMU）传感器ADIS16470和PNI的地磁传感器RM3100构建的捷联惯性导航系统（SINS）。实现了基于磁性、角速率和重力 （MARG） 的 SINS 的一些基本过程，包括电磁罗盘校准、使用扩展卡尔曼滤波器 （EKF） 的姿态和航向参考系统 （AHRS） 以及迹线跟踪。还实现了使用最小平方误差（MSE）方法的传感器融合松散耦合。显示了每个工艺步骤中的算法和实验设置。本文末尾讨论了结果分析和用于提高准确性的方法。

介绍

随着服务机器人的市场和技术的增长，导航已成为研究应用的热点。与车辆、轮船或飞机相比，服务机器人体积小，成本低，因此它们的导航系统应该是捷联和低成本的。传统的稳定平台导航系统通常涉及单独的加速器和光纤或基于激光的陀螺仪，所有组件都机械和刚性地安装在与移动车辆隔离的稳定平台上。这导致了体积大、可靠性差、成本高的缺点。相比之下，在捷联导航系统中，惯性传感器直接固定在车身上，这意味着传感器与车辆一起旋转。这种捆绑式方法消除了稳定平台导航的缺点。但是，平台导航的准确性通常高于SINS。平台导航通常可以达到战略级（0.0001°/hr陀螺仪偏置，1μg加速器偏置）或军用级（0.005°/hr陀螺仪偏置，30 μg加速器偏置），而大多数SINS只能达到导航级（0.01°/hr陀螺仪偏置，50μg加速器偏置）或战术级（10°/hr陀螺仪偏置，1 mg加速器偏置）。对于大多数服务机器人或AGV导航应用，这就足够了。

有多种导航方法，包括机器视觉、GPS、UWB、带 SLAM 的激光雷达等。虽然惯性导航始终是导航中的重要组成部分，但使用 IMU。然而，由于这种传感器的局限性，例如偏置误差、跨轴误差、噪声，尤其是偏置不稳定性，惯性导航通常需要一个伙伴传感器来定期为其提供参考或校准，这在这里称为传感器融合。有许多传感器可以与IMU融合，例如相机和里程表，但是在这些传感器中，地磁传感器是与IMU一起获取姿态的低成本方法。

在本文中，我们使用ADI公司的IMU、ADIS16470和地磁传感器来开发平台和算法，以实现捷联惯性导航系统。但是，传感器只能提供姿态信息。对于航位推算或距离测量，我们只能使用 IMU 中的加速度传感器。

ADIS16470 IMU简介

ADI公司的ADIS16470是一款微型MEMS IMU，集成了3轴陀螺仪和3轴加速度计。它为陀螺仪提供 8°/hr 偏置稳定性，为加速度计提供 13 μg 偏置稳定性，同时其关键参数经过工厂校准。此外，ADIS16470的低成本价格在同电平器件中具有吸引力，并被许多客户广泛使用。在本文中，我们使用微控制器通过SPI接口与ADIS16470通信。

地磁传感器简介

地磁传感器是用于测量指南针体坐标（即框架）中的地磁场的传感器，它为航向提供绝对参考。其 x、y 和 z 分量值是从当地地磁场投影而来的。这种传感器有两个主要缺点，一个是它的精度和分辨率不能很高，例如，霍尼韦尔常用的罗盘传感器HMC5883L只有12位分辨率。另一个缺点是传感器很容易受到周围环境的干扰，因为地磁场非常弱，从毫高斯到8高斯。

尽管存在这些缺点，但它仍然可以在许多情况下使用，例如露天场地、低 EMI 环境等。通过将地磁传感器松散耦合到IMU，我们可以在大多数环境中使用它。

在本文中，我们使用PNI传感器公司的高性能指南针传感器RM3100，提供24位分辨率。PNI使用有源激励方法来提高抗噪声能力。

罗盘传感器的校准

在使用指南针传感器之前，需要对其进行校准以消除两个主要误差。一种是失调误差，最初是由传感器和电路的失调误差引起的。另一个是比例错误。这两种误差都很容易受到周围磁环境的干扰。例如，如果传感器上施加了x轴方向的外部磁场，则会发出外部x轴偏移误差。同时，x 轴刻度也将不同于 y 轴和 z 轴。

通常用于校准磁传感器的方法是将传感器旋转为 x-y 平面上的圆，然后绘制数据。一个地方的地磁场强度是一个常数值，所以绘制的数据应该是一个圆;但是，实际上，我们将看到一个椭圆形，这意味着我们需要将椭圆移动并重新缩放为以零为中心的圆。

上面提到的2D校准方法有一些缺点，需要一个加速器来测量其倾斜度。我们使用3D球面拟合方法来校准罗盘传感器。首先，我们需要将传感器旋转到 x-y-z 空间中的每个方向，并在 3D 坐标中绘制其值。然后，我们需要使用最小平方误差（MSE）方法将数据拟合为椭球体。

椭球方程可以表示为

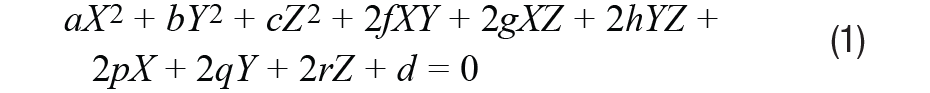
其中 X、Y 和 Z 是指南针在其三个方向上输出的地磁分量。将这些值拟合到椭球体意味着我们需要获得系数的最佳值集。我们将系数定义为：

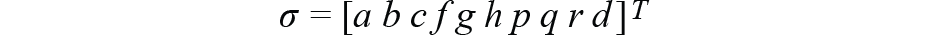
拟合时，我们将向量定义为：

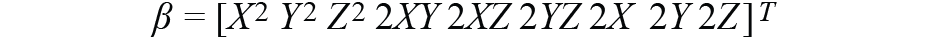
因此，我们需要计算一个最佳σ，并使用公式 2 找到最小值：

这样我们就可以得到如图 1 所示的拟合结果。

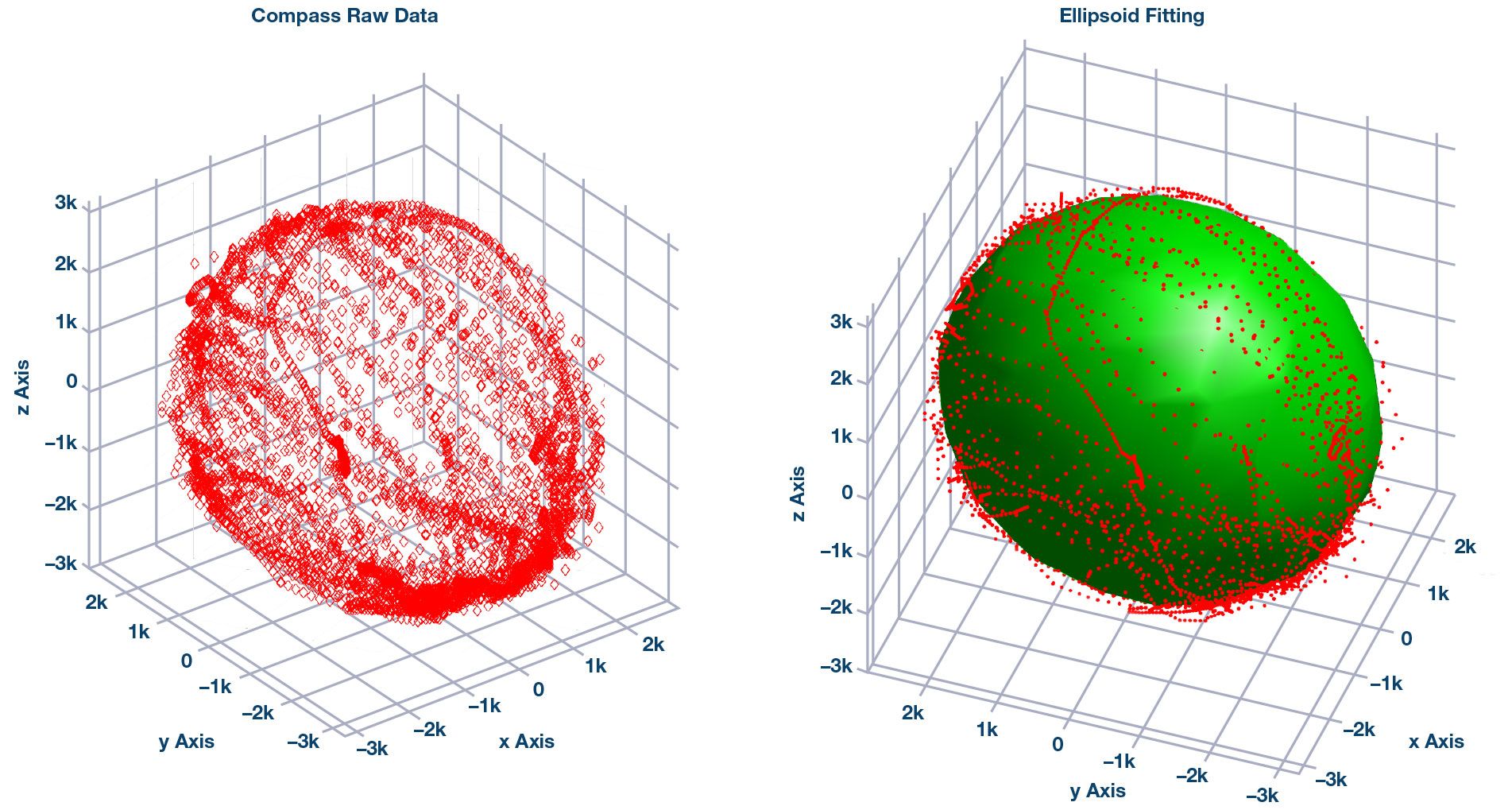
图1.原始罗盘数据分布（左）和使用椭球拟合后的罗盘数据（右）。

为了校准传感器，我们需要将拟合的椭球体拉伸并移动到以零为中心的球体上。我们使用矩阵奇异值分解（SVD）方法来进行此校准。校准后球如图2所示。1,2

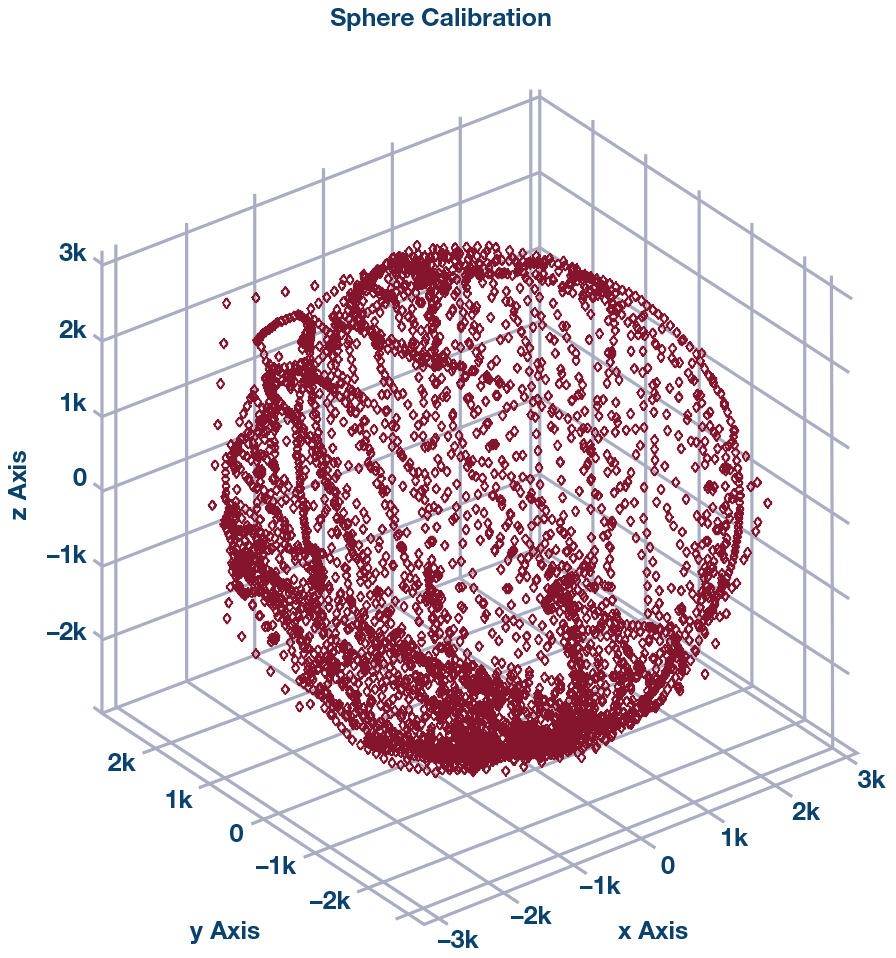
图2.使用SVD方法进行球体校准后的指南针数据。

校准后，我们可以看到测量的磁场强度（球体半径）将保持在几乎恒定的值，如图3所示。

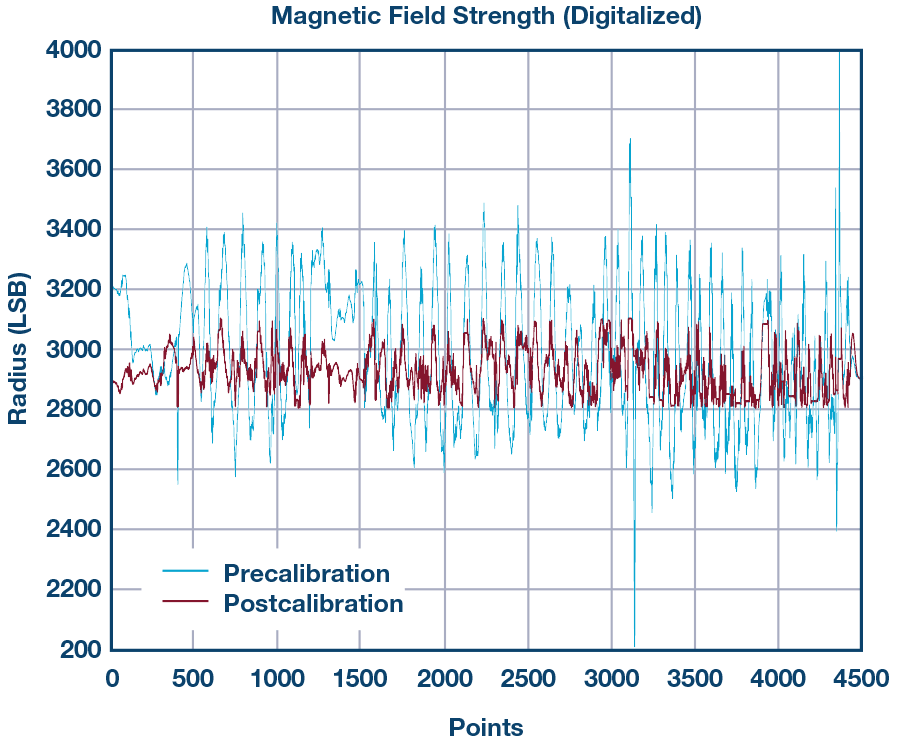
图 3.校准前和校准后校准之间的磁场比较。

使用ADIS16470和指南针的姿态和航向参考系统

AHRS 由三个轴上的传感器组成，这些传感器提供姿态信息，包括横滚、俯仰和偏航。AHRS是飞机导航的一个概念。我们用它来描述方向;也就是态度。

在介绍我们的方法之前，有必要先解释一下融合的原因，先找到态度。事实上，现在我们的系统中有三种传感器：陀螺仪、加速器和指南针。

陀螺仪给出围绕每个轴的角旋转速率。通过积分角速率，我们可以找到旋转角度。如果我们知道初始标题，我们将始终得到标题态度。由于集成，陀螺仪的不稳定偏置会累积，从而导致角度误差。此外，来自陀螺仪的高斯分布噪声将被积分到布朗运动过程中，并导致随机行走误差。因此，我们很难长时间使用陀螺仪，陀螺仪需要定期校准。

加速器提供每个轴方向的运动加速度。在静态状态下，我们可以得到每个轴之间的角度和重力加速度。由于重力加速度在方向和值上是恒定的，因此我们可以得到相对于重力方向的航向姿态。但是，该方法以重力加速度为参考，因此无法求解围绕重力加速度旋转的角度。

指南针提供从地磁场投射的每个轴上的值。我们可以从每个轴与地磁场方向之间的关系中推导出角度值，这也是一个常量矢量。如上一节所述，由于对外部磁场的抗扰度差，指南针需要低干扰环境。

从这个解释中，我们可以看到，仅仅依靠一个传感器来找到姿态是很困难的，我们需要将两个或三个传感器组合使用并融合信息。本文涉及加速器、陀螺仪和地磁罗盘来寻找姿态。这种融合被称为磁、角速率和重力（MARG）系统。

扩展卡尔曼滤波器设计和传感器融合

有多种方法可以将 IMU 和指南针数据融合在一起，例如互补滤波器、统计 ARMA 滤波器、卡尔曼滤波器等。在本文中，我们使用扩展的卡尔曼滤波器。

首先，我们需要介绍本文中使用的一些定义。

坐标定义

标题或方向是两个坐标（即框架）之间的关系。一个坐标总是在变化，另一个坐标保持不变。对于坐标定义方法，我们使用导航坐标和正文坐标。与东北向下 （NED） 或地理方法相反，我们将测量的初始主体坐标值定义为导航坐标，之后是一个常量坐标。从正文坐标到导航坐标的映射（投影）矩阵定义为

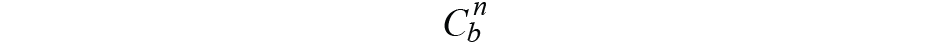
态度定义

与欧拉角或方向余弦矩阵（DCM）矩阵不同，我们在这里使用四元数，定义为

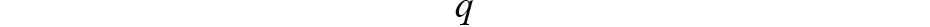
这通常用于导航以避免争论。3

使用卡尔曼滤波更新姿态

我们在本文中使用的运动学方程，即状态转移方程是一种偏差格式，它不是线性的，因此我们需要使用具有一阶线性近似的 EKF 来表示偏差方程。对于 EKF 设计，我们定义

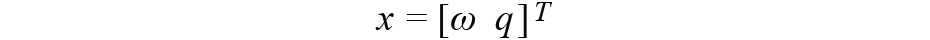
一个 1 × 7 向量作为状态变量，其中

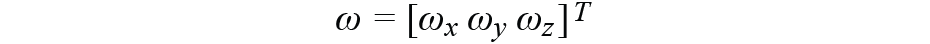
是角速率，并且

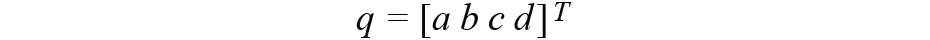
是态度四元数。

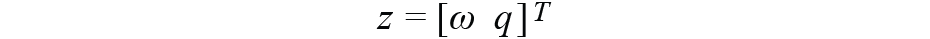
1 × 7 向量是观测变量，它与状态变量具有相同的分量。

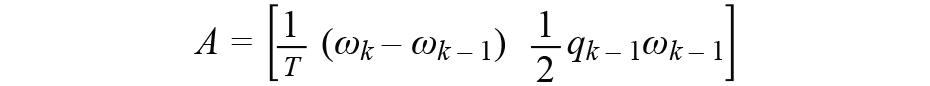
一个7×7矩阵，是状态转移矩阵，其中A的第一部分是角速率的数字化微分方程，第二部分是数字化的四元数更新方程，由运动学方程推导出来。

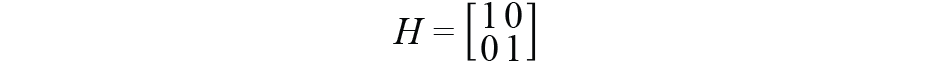
7×7矩阵是观测矩阵。

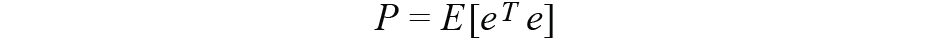
是误差协方差矩阵，一个 7 × 7 矩阵，其中

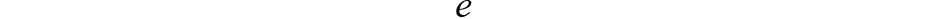
是从实数 x 估计的误差向量 x̂。我们在测试中将初始误差设置为相对较小的值。它将自动收敛到一个小值。

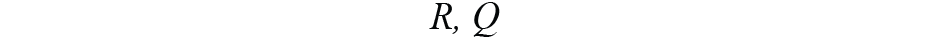
设置为状态转换噪声和观测噪声的噪声协方差。我们得到它们的初始值，

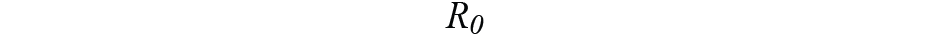
和

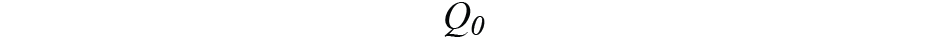
通过测量陀螺仪和加速器的交流均方根值的平方。在保持 IMU 和指南针处于静态状态的同时，我们设置

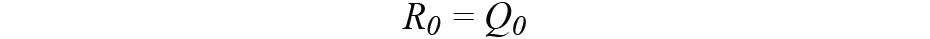
有了这个定义，我们的卡尔曼滤波器将通过以下五个步骤完成：

步骤1：使用公式3计算卡尔曼增益K：

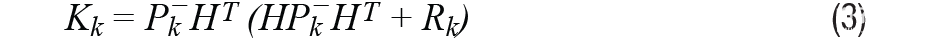
第 2 步：计算误差协方差矩阵 P：

步骤3：输出估计状态，x̂：

第 4 步：预测状态，x̂–:

步骤5：投影误差协方差矩阵，P–:

该过程可以简单地描述为图4中的框图。

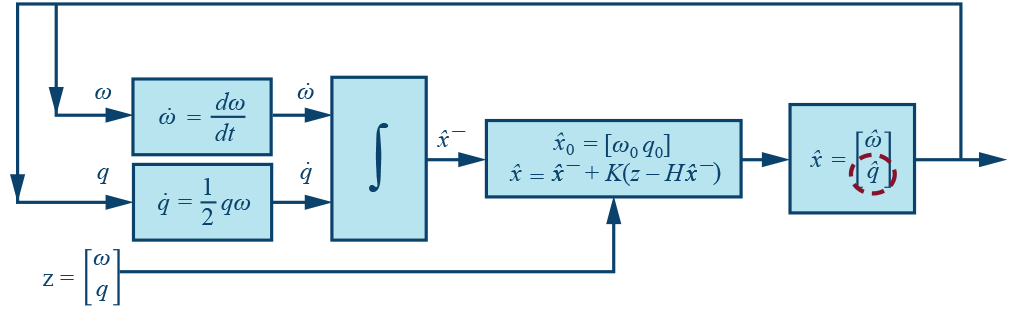
图4.用于更新态度的卡尔曼滤波流程图。

基于MSE的传感器融合

在上一节中，观测变量为

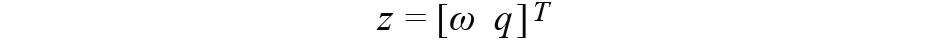
其中没有来自指南针的信息。由于ω是角速率，我们只能使用四元数来导入罗盘数据q。我们使用MSE方法得到q，即观测变量中的分量。

我们定义变量如下：

mb和一个b：体框内的罗盘磁力值和加速度值。

mn和一个n：导航框中的罗盘磁值和加速度值。

mn0和一个n0：导航坐标系中的初始静态罗盘磁值和加速度值。

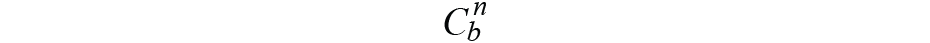
是从车身框架到导航框架的姿态变换矩阵，用四元数表示，可以写成

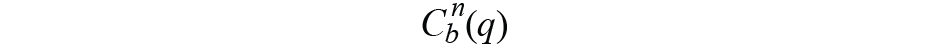
这给了我们导航框架中的初始值与从正文框架实时映射到导航框架的值之间的误差，ε。

基于前面的定义，MSE方法可用于获得最佳

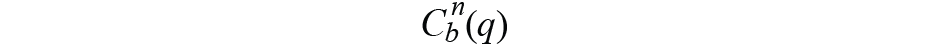
通过最小化公式8：

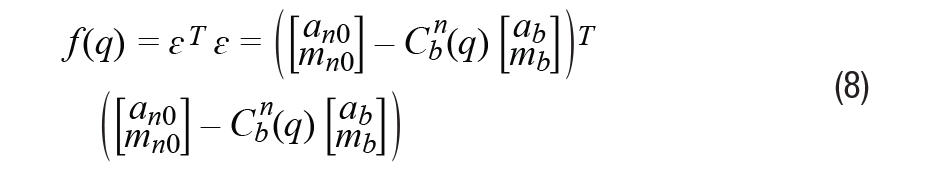
通过取 f（q） 的推导并使其等于零，

我们将得到方差含义的最佳 Q。我们使用高斯-牛顿方法求解上述具有一阶梯度收敛的非线性方程。

通过结合角速率，我们将得到观测变量，

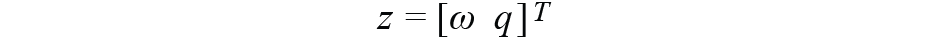
在卡尔曼滤波器中融合了指南针数据和 IMU 数据。

该过程可以通过图5中的框图简单描述。

图5.使用 MSE 方法的传感器融合框图。

松耦合

如前所述，我们经常遇到无法使用指南针传感器的情况。如果磁数据受到干扰，求解的姿态精度将比仅使用IMU时差。因此，我们使用松耦合来判断磁性传感器是否可用。当磁性传感器不可用时，我们将仅使用 IMU 来查找姿态，当磁性传感器可用时，我们将使用融合算法来查找姿态，如图 6 所示。

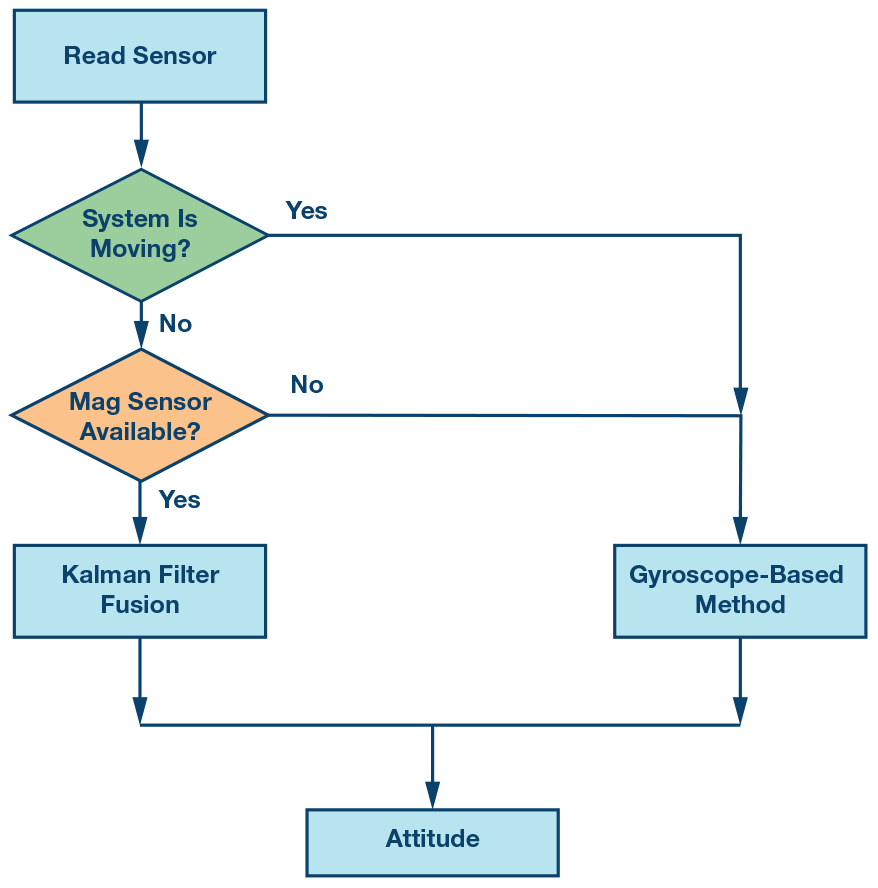
图6.姿态计算流程图。

在获得新数据后，或者在新的姿态求解周期中（在某些系统中，采样周期与姿态解析周期不同，但我们在这里进行单样本周期解析），我们计算加速度的大小。如果它不等于 1 g，我们将不使用加速器的输出进行姿态计算。然后我们计算指南针输出的大小，并将其与初始值进行比较。如果它们彼此不相等，我们将不会在此循环中使用地磁传感器的数据。当两个条件都满足时，我们将使用卡尔曼滤波器并进行MSE融合。

使用ADIS16470的航位推算（DR）

在导航中，航位推算是通过使用先前确定的位置计算当前位置的过程，并根据已知或估计的速度或加速度在解析周期内推进该位置。此处将使用ADIS16470加速器。根据上一节中解析的姿态，我们得到捷联系统的移动方向，然后我们需要计算方向上的距离，最终确定位置。

航位推算方法介绍

捷联航位推算需要使用基于加速度测量的特定力方程跟踪INS的位置。比力方程可以简单地描述为公式10、公式11和公式12：

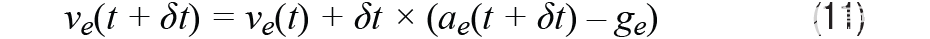
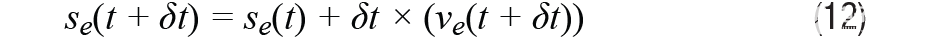
哪里一个e是地球框架中的加速度，一个b是身体框架中的加速度，ve是地球坐标系中的速度，se是地球坐标系中的距离，ge是地球坐标系中的重力加速度，以 g 为单位为 [0 0 1]。我们需要强调的是，地球框架与导航框架不同——地球框架是面向NED的。这个δt是解析周期。

第一个方程找到从 IMU 体框架到地球框架的加速度投影，如格式所示。

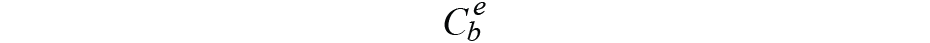
第二个方程将加速度积分或累积为速度;但是，由于测量的加速度涉及重力分量，因此需要减去重力。

与公式11类似，公式12将速度积分到距离中。

传统方法存在几个问题。

加速器输出总是有偏置，偏置与重力相结合，因此很难在公式10中减去，因此更准确的表达式应该是：
 

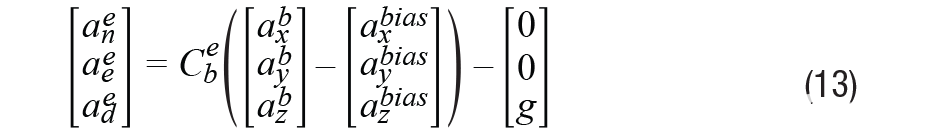
除非使用一些专业设备，例如分界针。

传统方法的数值积分法，通常采用零阶持有者法（前一个值）进行积分。但是，对于连续运动，这将引入明显的误差。例如，让我们比较以下方法：

方法一：

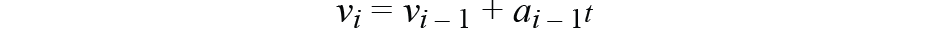
（零阶持有者）

方法2：

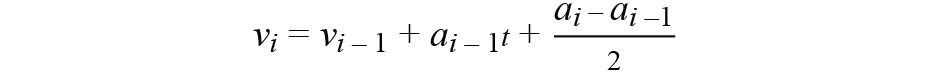
（线性插值）

加速度为 0.5 m/s2在 5 秒内，位移将相差 4 m。仿真结果如图7所示。

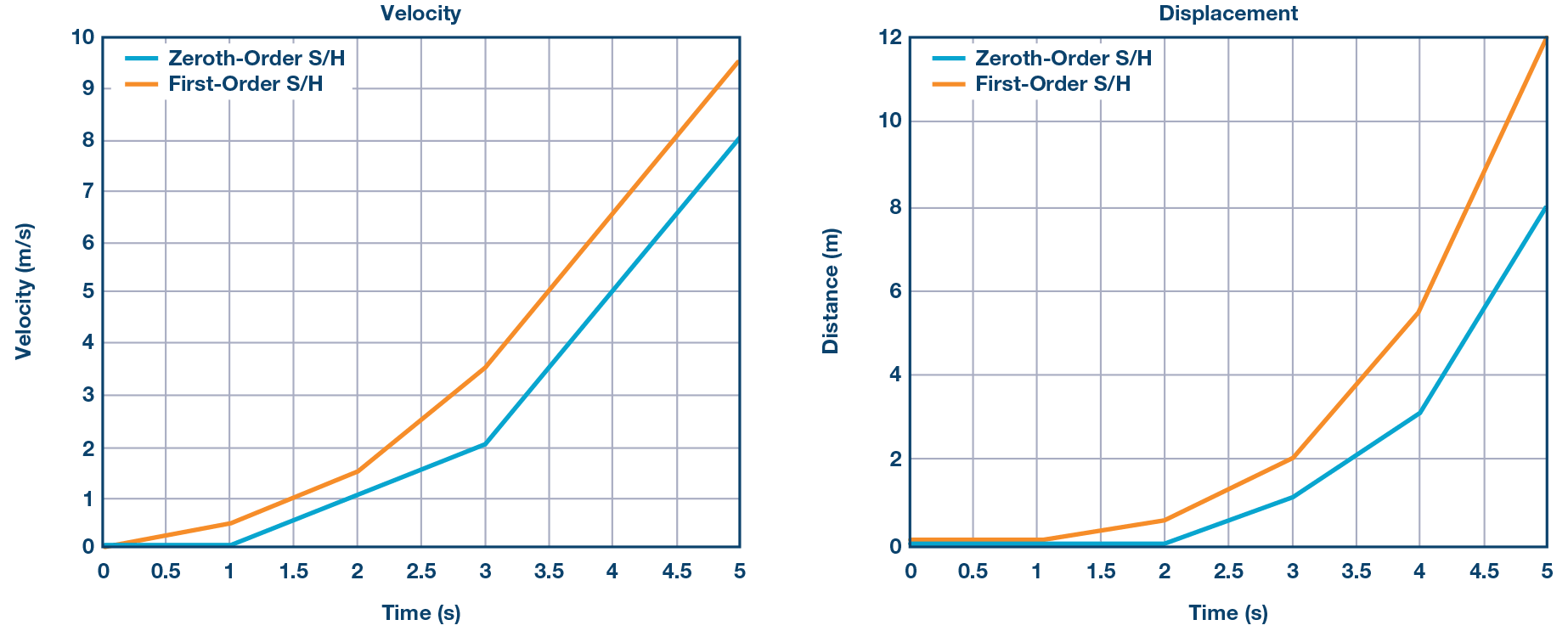
图7.速度计算中零阶积分方法与一阶积分方法的比较.

基于前面的讨论，我们修改了传统比力方程的两点：

我们不使用地球坐标作为导航框架。相反，正如我们在寻找先前的态度时所做的那样，我们使用最初的态度

作为导航框架。通过这种方式，偏差和重力都可以很容易地消除，如公式14所示：



虽然偏置和重力分量包含在初始姿态中，但这样我们就不需要将它们分开来得到每个分量，而是可以直接减去它们。

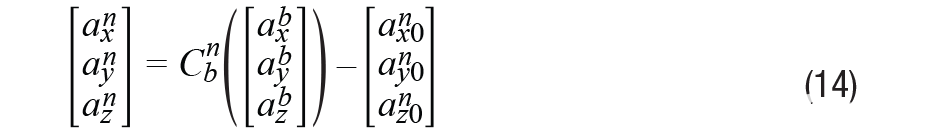
与零阶持码和一阶插值相比，我们使用一阶来获得更准确的积分结果。

运动学模式和零速更新技术（ZUPT）

通过使用 IMU 的初始值作为导航框架，我们可以部分抵消加速器的初始偏置影响。但是，即使我们可以在使用设备之前使用分频头准确测量偏差，仍然很难消除，除非我们使用另一个精确的传感器定期校准它。这主要是由两部分引起的：一是偏置不稳定性，这意味着我们之前测量的偏置不是现在的实际偏置。另一种是速度随机游走，这是加速度不可或缺的一部分。前面提到的不良特性会使我们计算的距离漂移显着。即使我们停止移动并保持静止，加速度积分的速度仍然存在，距离仍然会增加。

为了解决这个问题，我们需要找到一种通过使用ZUPT技术重置速度的方法。ZUPT技术紧密依赖于应用，因此我们需要获得系统和应用的运动学特性，然后为我们的算法给出一些规则。我们发现的运动学模式越多，我们的结果就越准确。

我们通过移动带有SINS系统的转椅来应用我们的实验。由于我们的研究不仅限于特定应用，因此我们使用以下运动学假设：

对于航位推算，导航框架中没有 z 轴移动。此限制仅用于航位推算，不用于姿态解析。显然，我们正在2D空间中移动系统。这有助于消除 z 轴误差。

所有转弯都在停止后发生。如果在移动时发生转弯，姿态解析将受到干扰，因为将涉及额外的加速度。

如果系统正在移动，加速度不能保持不变超过 500 毫秒。速度不能保持不变超过 2 秒。由于我们正在推转椅，因此很难手动保持力准确不变超过500毫秒，人类也很难以匀速持续推动转椅超过2秒。事实上，我们正在使用此规则来执行ZUPT。

加速度不能大于±1米/秒2.这个规则用于一些噪音过滤，这是基于我们对椅子的拉力或推力，不会很大。

如图 8 所示，当系统沿 X 方向移动时（投影到导航帧后），Y 方向也会产生加速度，积分后，Y 方向速度不会为零，这意味着即使我们只在 X 方向移动，航位推算系统仍然会给我们 Y 分量。

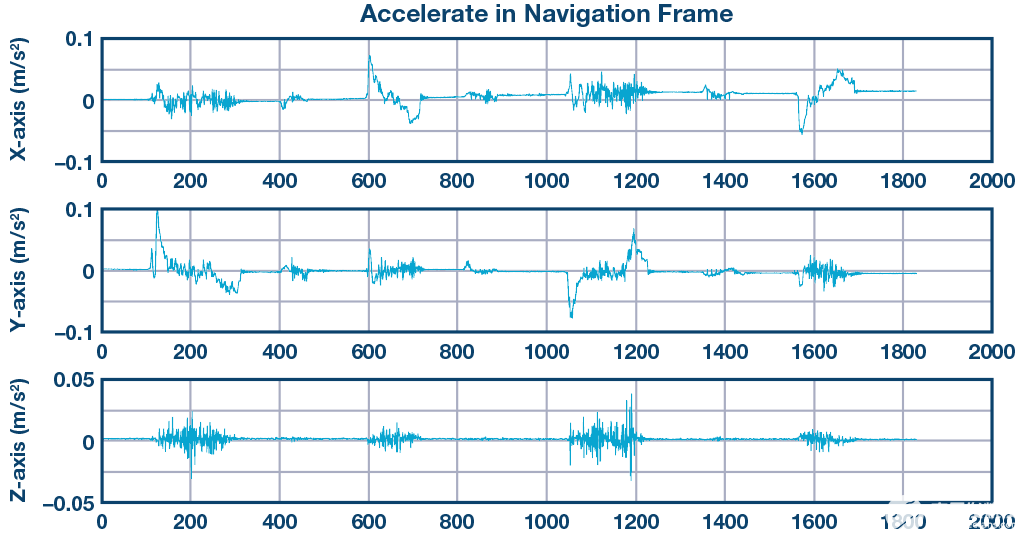
图8.导航框架中三个方向的加速度。

基于第三个运动学假设，我们可以使用ZUPT来消除这个误差。ZUPT后的积分速度如图9所示。

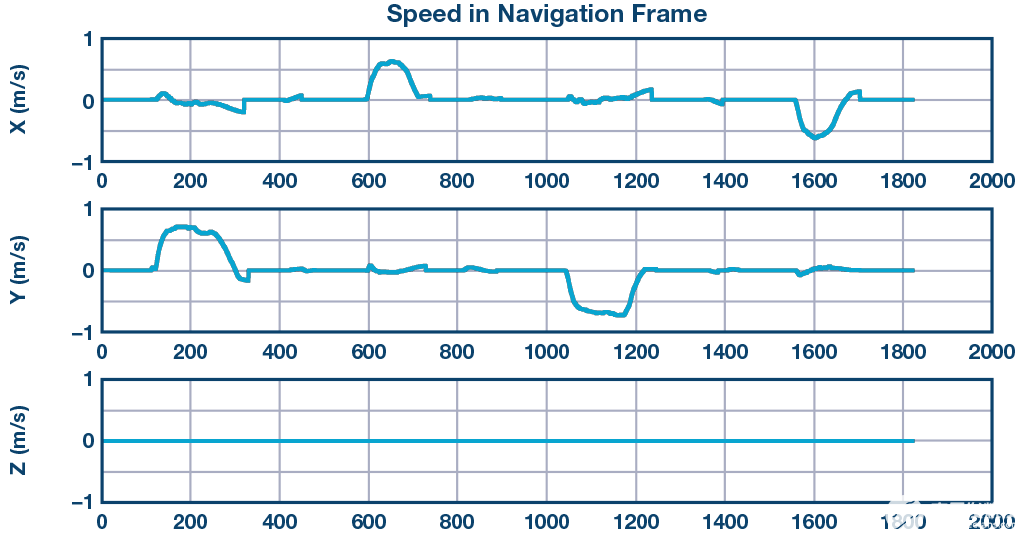
图9.导航框架中三个方向的速度。

尽管我们使用了第三个假设，如前所述，但仍然无法完全消除该错误。误差消除取决于设置的零加速度和零速度的阈值。但是，大多数错误已得到纠正。

基线移位取消

尽管使用了ZUPT，但有时仍可能无法达到零加速度。这导致两个因素：

我们不能使用ZUPT完全消除偏置不稳定性误差和速度随机游走。

我们解决的姿态有一些误差，这将导致投影（从车身框架到导航框架）加速度误差。

以图 10 为例。图10中的左图是ADIS16470的原始数据（主体框架），图10中的右图是导航帧中预测的加速度。可以看出，当它停止运动时，预计加速度不为零。由于它总是在变化，我们称之为基线转移。

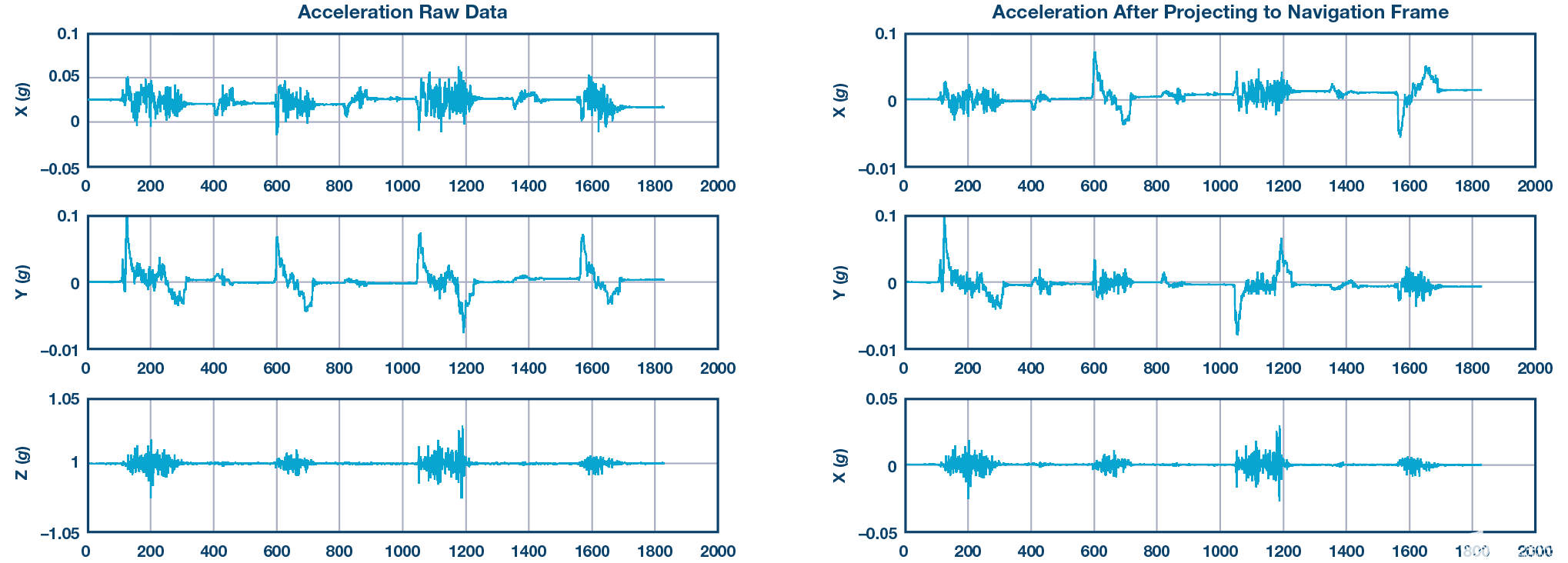
图 10.车身框架（左）和导航框架（右）中的加速度。

为了消除基线偏移，我们需要实时连续获取偏移偏差，并将其从预计加速度中减去。结果如图 11 所示。

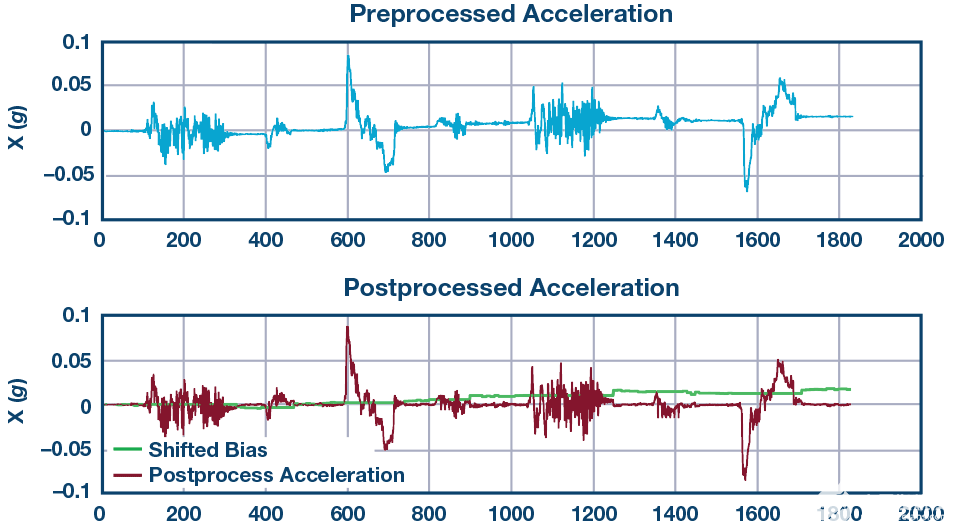
图 11.基线偏移消除之前（顶部）和之后（底部）的加速度。

上图是基线偏移消除前的加速度，下图中的绿色轨迹是我们计算的基线偏移，红色曲线是基线偏移取消后的加速度。

航位推算过程可以使用图 12 中的框图简要描述。我们输入车身框架加速度一个b和态度转换矩阵（来自 AHRS）

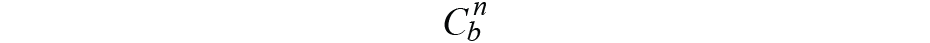
到灾难恢复系统。完成此操作后，我们将在导航框架中获得位置。

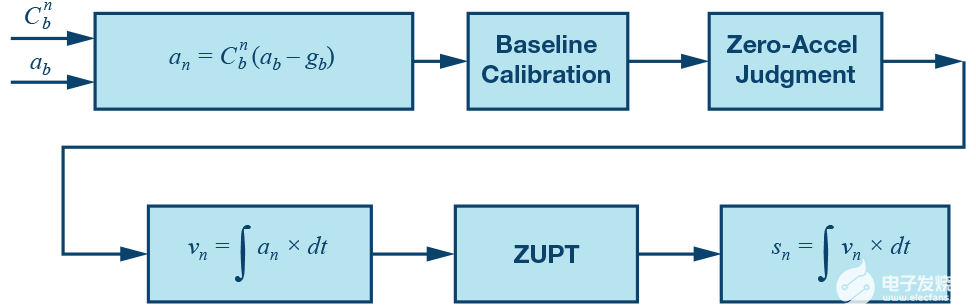
图 12.航位推算的流程图。

实验结果及结论

实验结果

如图13所示，我们使用SPI端口将ADIS16470评估板和RM3100罗盘评估板连接到ADI的ADuCM4050板，从而构建系统。ADuCM4050调整数据格式并进行时间同步（因为IMU和指南针的数据速率不同）。然后使用UART将捕获的数据传输到计算机。所有计算，包括校准、AHRS 和 DR，都在 MATLAB 中执行。®

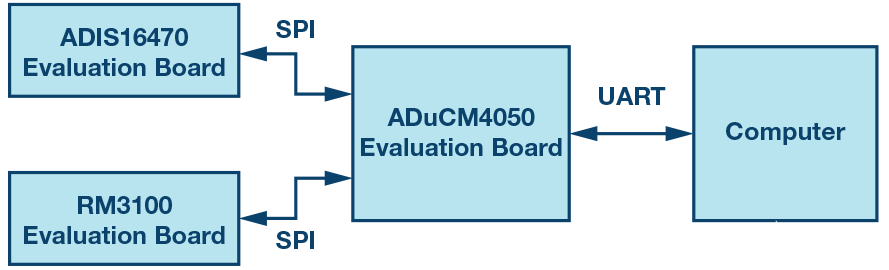
图 13.实验平台设置。

该实验是通过将电路板和计算机放在转椅上并在我们的实验室中将转椅推一圈来实现的。

AHRS输出：姿态以四元数格式和DCM格式显示，如图14所示。

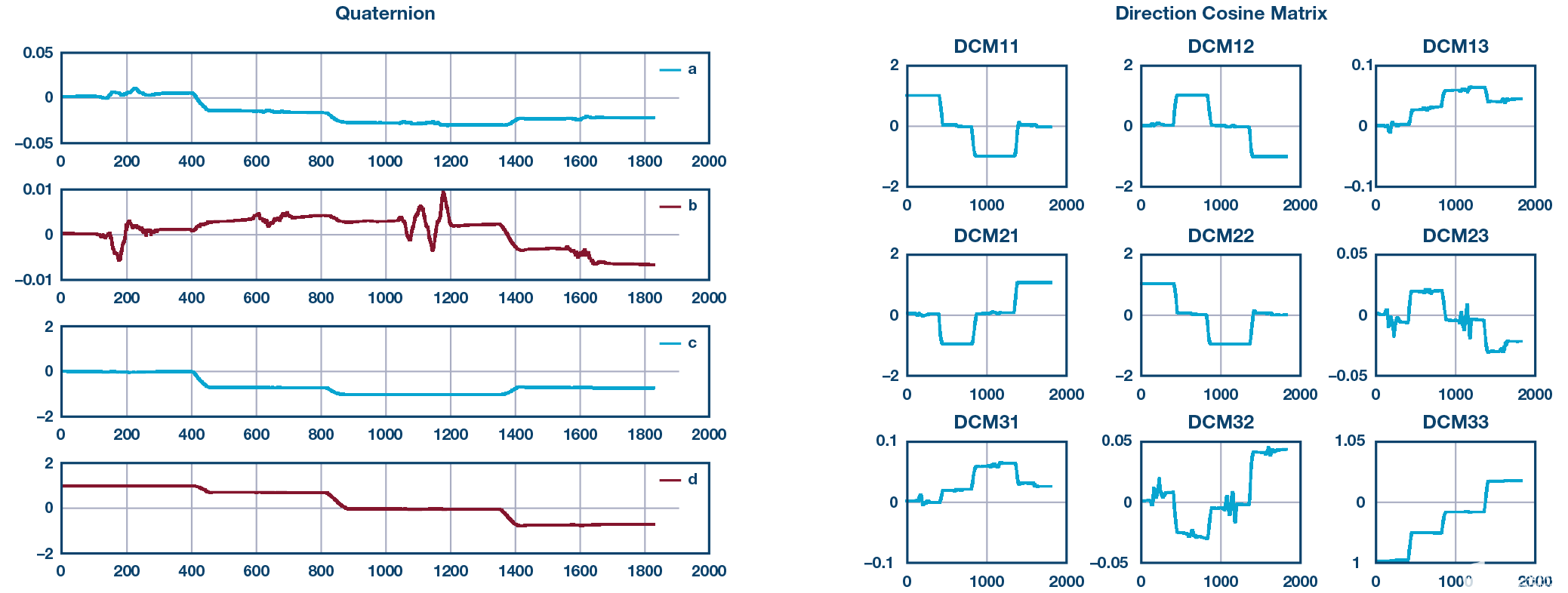
图 14.四元数格式（左）和DCM格式（右）的姿态。

DR 输出：具有 X-Y-Z 位置和 3D 图的航位推算结果如图 15 所示。

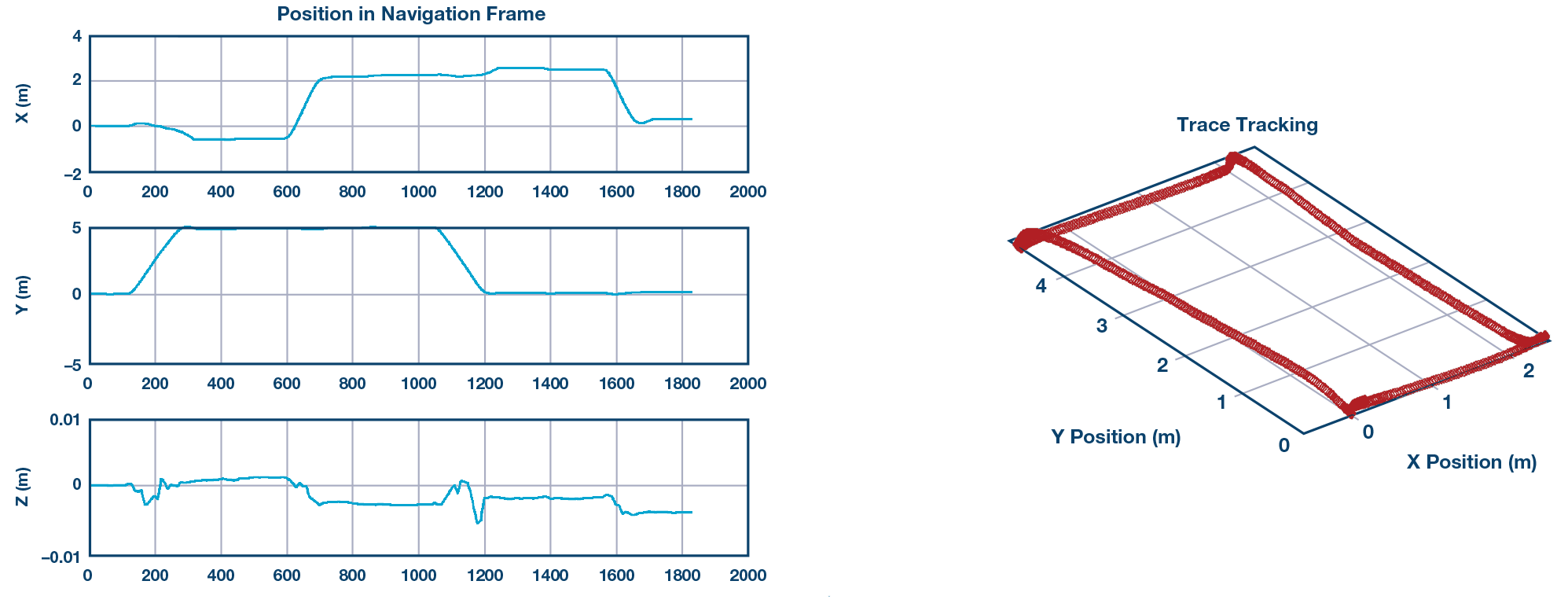
图 15.仓位计算结果。

结论

本文介绍了使用ADI公司的IMU ADIS16470和地磁传感器RM3100构建导航系统的基本过程，介绍了我们使用的校准、AHRS和DR方法。在平台和实验环境等条件有限的情况下，我们很难进一步测试平台和算法。

有很多方法可以用来改善结果，例如：

使用里程表或 UWB 距离测量将加速器与 IMU 融合，以获得更好的 DR 距离。

使用更复杂的运动学模型，在AHRS和DR中涉及传感器级别和系统级别的更多特性，例如系统的振动，加速度和减速模型，地面平整度等。这意味着为我们的计算提供更多的边界条件，以获得更准确的结果。

使用更精确的数值计算方法，如使用辛普森法则或三次样条插值在DR中进行积分，或者使用牛顿法代替高斯-牛顿法求解非线性MSE方程等。

我们在实验中发现的最后一点，也是最重要的一点是，INS与应用或运动学模式密切相关。例如，我们在两个地方进行了实验：一个没有地毯的实验室和一个铺有地毯的办公室。如果我们使用相同的参数集，DR 结果显示出巨大的差异。因此，无论是哪种应用，如患者跟踪、AGV导航、停车定位，还是针对同一应用中的不同工况，我们都需要全面了解其运动学模型。

审核编辑：郭婷