

数字电源中如何把连续频域变换为离散域(一)
描述
从事开关电源研发的工程师,尤其是模拟控制的电源设计师,比较熟悉连续时域、连续频域的传递函数分析。那如何把模拟控制变成数字控制呢?因为计算机或者CPU它本质上是一个采样系统,只能处理离散系统,所以要把连续域变换成离散域,并且离散域的方程才能成为差分方程的形式,也只有差分方程才好写成C代码控制。我们今天分享,如何把连续频域变成离散域的其中一种变换方法:Tustin变换法(双线性变换法),这也是实际研发中非常常用的一种变换方法。
我们开始举例,已知连续校正环节传递函数D(s)为:
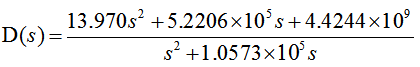
其中变换器的开关频率为fs=250kHz。如何设计双线性变换法所得的离散控制器D(z),并比较D(s)与D(z)的频率特性呢?
1)先利用matlab把D(s)离散成D(z):
① Tustin变换法(双线性变换法):
fs=250000;
T=1/fs;
Ds=tf([13.970 5.2206e5 4.4244e9],[1 1.0573e5 0]);
Dz=c2d(Ds,T,'tustin')
Transfer function:
12.41 z^2 - 23.03 z + 10.68
z^2 - 1.651 z + 0.6509
Sampling time: 4e-006
2)利用matlab绘制离散控制器D(z)的频率特性,代码如下:
T=4e-6;
w=0:1:4*pi/T;
f=w/2/pi;
num_d_s=[13.970 5.2206e5 4.4244e9];
den_d_s=[1 1.0753 0];
num_d_z=[12.41 -23.03 10.68];
den_d_z=[1 -1.651 0.6509];
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_s,p_d_s]=bode(num_d_s,den_d_s,w);
[m_d_z,p_d_z]=dbode(num_d_z,den_d_z,T,w);
subplot(2,1,2),plot(f,p_d_s,'-',f,p_d_z,'-');
xlabel('Frequency(Hz)'),ylabel('phase(deg)');
axis([0 2/T -100 100]);
grid on;
subplot(2,1,1),plot(f,20log10(m_d_s),'-',f,20log10(m_d_z),'-'),title('BodeDiagrams');
xlabel('Frequency(Hz)'),ylabel('Magnitude(dB)');
axis([0 2/T 0 40]);
grid on;
3)连续控制器D(s)与离散控制器D(z)的频率特性如下图1:
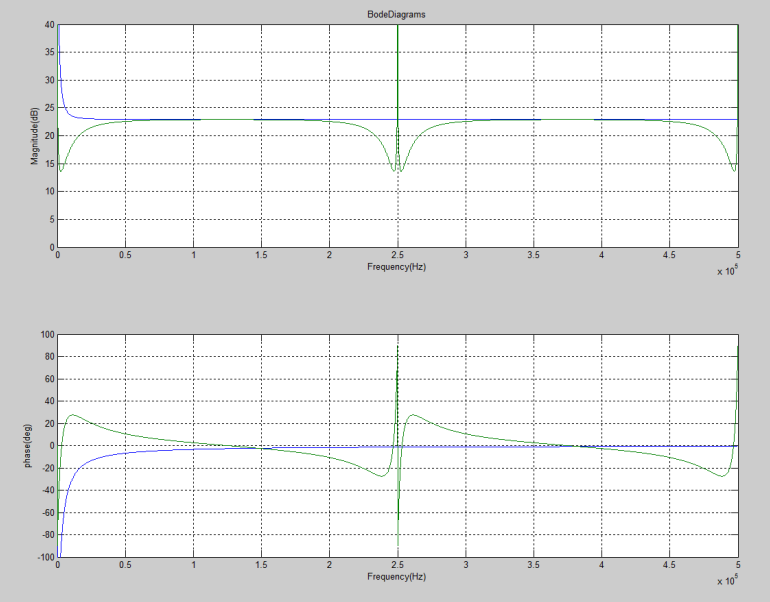
图1 仿真图
以上就是 Tustin变换法(双线性变换法)的简单过程,简单的3个步骤,既可以得到连续域与离散域的仿真图,是不是很简单呢?另一个问题,数字控制还有其他变换方法吗?有的,并且在实际产品开发中也比较常用,我们下次继续分享。
-
实序列的z变换为什么会出现一对相互共轭的复数零点?2023-11-08 4645
-
傅里叶变换对信号处理的意义2023-09-07 3493
-
使用快速Fourier变换法将ADC样本转换为频域频谱的方法和结果2023-08-22 391
-
数字电源中如何把连续频域变换为离散域(二)2022-12-23 2809
-
傅里叶变换是把时域中的非周期连续信号,转换成了频域中的非周期什么性质的信号?2020-07-22 2898
-
图像频率域分析之傅里叶变换2019-05-22 2327
-
离散信号的频域分析之傅里叶变换的应用2019-04-16 11704
-
有限长离散变换-离散傅里叶变换2011-02-23 1227
-
一种基于离散小波变换和HVS的彩色图像数字水印算法2009-09-19 6339
-
连续时间LTI系统的复频域分析.ppt2009-09-16 4116
-
连续时间LTI系统的复频域分析视频教程2009-09-03 850
-
离散时间信号和离散时间系统2008-10-30 1040
全部0条评论

快来发表一下你的评论吧 !

