何为滤波？粒子滤波是怎么来的？

一、前言

粒子滤波（particle filter）是一种常见的滤波算法，广泛应用于目标跟踪、移动机器人等领域。网络上有不少关于粒子滤波的资料，但大多是直接给出了粒子滤波的相关公式和证明，或较为直观上的解释。作者在学习粒子滤波的过程中对一些概念和操作时常感到突兀，后来发现想要完整了解粒子滤波，需要首先了解前因，逐渐深入才能理解粒子滤波，而不是直接学习粒子滤波这个方法。

本文将侧重从“粒子滤波是怎么来的”这个问题介绍粒子滤波。限于篇幅与易懂性，对一些概念并没有展开介绍，读者在了解基本思路后可以根据给出的资料深入学习。本文包含了作者自己不严谨的理解与阐述，如有疏漏，望批评指正。

二、对“滤波”的一些介绍

2.1 何为“滤波”？

贝叶斯滤波、卡尔曼滤波、粒子滤波……种种这些滤波方法，都涉及到了“滤波”这个词。那么到底什么是滤波，不同的领域有不同的定义。比如在信号系统领域，滤波是指将信号中特定波段的频率滤除的操作。而在移动机器人领域，我暂时没有看到较为严格的定义。我认为可以姑且理解为：通过不断地观测，使得对目标状态的估计变得更加准确。

2.2 贝叶斯滤波

卡尔曼滤波与粒子滤波都是基于贝叶斯滤波框架下的滤波算法。讲粒子滤波便不得不提贝叶斯滤波。贝叶斯滤波的基本思想是根据上一时刻的状态对当前状态进行预测，并根据此时的观测进行更新。基本算法是：



（图片来源：《概率机器人》） 可以看出，在预测部分需要求一个积分，而这个积分往往很难求。所以显有方法可以直接利用原始的贝叶斯进行处理。

2.3 卡尔曼滤波

卡尔曼滤波也是非常庞大的一块内容，这里不展开介绍。只在这里说明，卡尔曼滤波是贝叶斯滤波在线性高斯系统下的一种滤波算法。而对于非线性系统，则衍生出来了扩展卡尔曼滤波。同时指出，无论是卡尔曼还是扩展卡尔曼滤波，都是参数化的滤波方法，对于无法用参数化进行表示的，则采用粒子滤波。粒子滤波是一种无参的滤波算法。

三、积分计算：从蒙特卡洛说起

3.1 分段近似法求积分

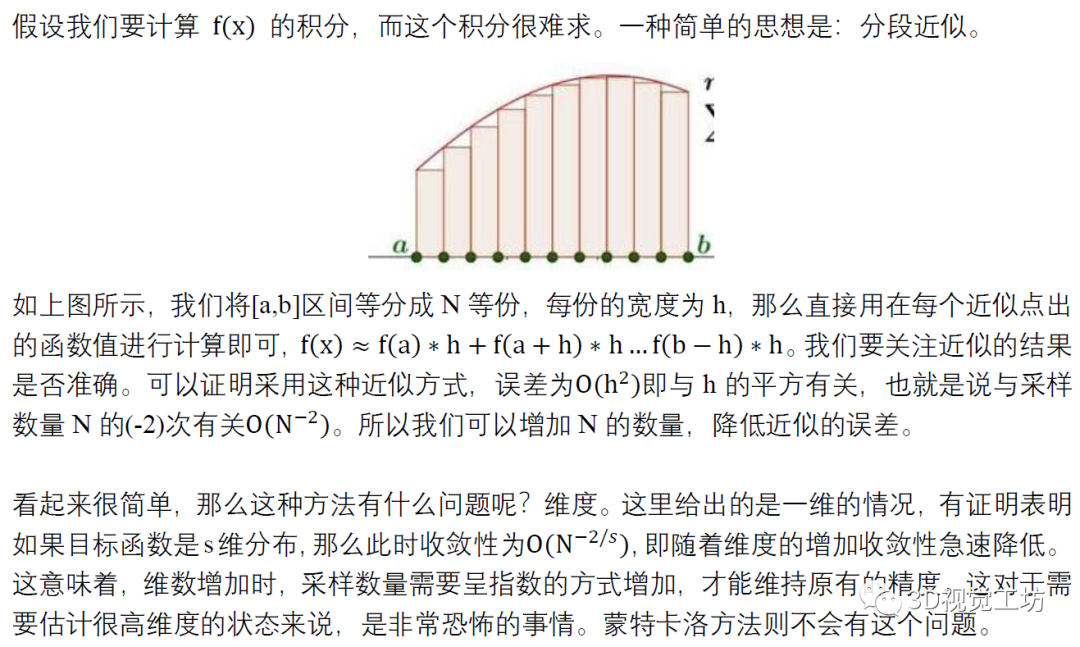
3.2 蒙特卡洛采样求积分

（此处略过蒙特卡洛基本原理）

3.2.1 简单的均匀采样

求积分和求期望是相同的。假设我们对一个分布求取积分，采用最简单的采样方式——均匀采样。我们求取在x满足均匀分布u(x)时，f(x)在[a,b]的期望I。按照分布u(x)进行N次随机采样：

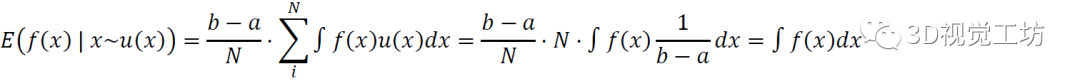
可以发现最后一项对f(x)的积分，就是x的期望。所以我们可以发现，当我们按照均匀分布u(x)对x进行大量采样，计算对应的f(x)的平均值，就是f(x)的积分。

3.2.2 任意分布的采样

下面我们研究，如果不是按照均匀分布u(x)采样，而是任意分布p(x)进行采样，结果如何。此时

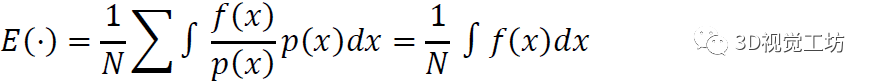
依旧与原始的积分相同。所以我们得出了重要的结论：在蒙特卡洛时，我们可以按照任意分布进行采样，再计算对应f(x)的积分。

这一点很好理解，如果我们选择的分布p(x)就是真实的分布，那么我们从p(x)进行采样，就和直接从真实分布进行采样是一样的，积分结果当然是没有误差的。这提醒我们，在选取p(x)分布时要尽可能的与实际分布接近，从而极大程度的降低方差，从而减少需要采样的数量。

四、重要性采样与序列重要性采样

4.1 重要性采样(Importance Sampling, IS)

4.2 序列重要性采样(Sequential Importance Sampling, SIS)

4.3 重采样(Resampling)

在实际过程中，我们发现利用权重更新公式进行更新时，在几次迭代之后，权重的分布会极其不均匀，出现个别粒子权重很大接近于1，而其他的都接近于0的情况。这时候采用了一种“重采样”策略，即每次权重更新之后，根据当前权重对所有粒子进行重采样，之后将所有权重设定为相同。这样我们用粒子的数量代替了粒子的权重，避免了权重的不均匀。

5. 粒子滤波(Particle Filter)

  此时对权重更新公式进行变形（在不产生歧义情况下部分内容用点省略）：

6. 总结

本文首先从滤波问题说起，指出了贝叶斯滤波框架下积分很难求的问题。由此引出蒙特卡洛方法。之后为了降低误差、减少运算量和避免权重集中，对应出现了重要性采样、序列重要性采样与重采样，顺理成章的得出了粒子滤波的数学原理，之后给出了对应的物理模型。最后给出了简单的粒子滤波的完整算法。





审核编辑：刘清