数字电子技术基础----逻辑函数的化简方法

1逻辑函数的化简方法

 本文通过具体题目来总结逻辑函数的化简方法：

总的来说包括两大部分：公式化简法和卡诺图化简法：

一、公式化简法

①并项法：AB + AB' = A

    例：

 

Y1 = A(B'CD)' + AB'CD = A[(B'CD)' + B'CD] = A;
Y2 = AB' + ACD + A'B' + A'CD = B'(A + A') + CD(A + A') = B' + CD;
Y3 = A'BC' + AC' + B'C' = A'BC' + (A + B')C' = A'BC' + (A'B)'C' = C';
Y4 = B(C'D + CD') + B(C'D' + CD) = B(C^D) + B(C^D)' = B;

 

    这种方法本质上是类似于合并同类项，将剩余部分构造成A + A’的形式；其中Y3和Y4需要稍微注意一下。

[注]^代表的是异或，()'代表的是取非。

②吸收法：A + AB = A

    例：

 

Y1 = ((A'B')' + C)ABD + AD = ((A'B')' + C)BAD + AD = AD;
Y2 = AB + ABC' + ABD + AB(C' + D') = AB + AB(C' + D + C' + D') = AB;
Y3 = A + (A'(BC)')'(A' + (B'C' + D)') + BC = A + (A + BC)(A' + (B'C' + D)') + BC = A + BC;

 

    其中，Y3中，化简出(A + BC)后，将式子乘开，则后面每一项中要么含有A，要么含有BC，所以，可以直接使用吸收法得出最后结果。

    吸收法的本质类似于数学中的大小集合问题，画个卡诺图来解释一下：

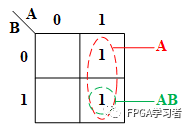
    可以看到，A的范围比AB要大，所以他们属于一个包含关系，在A为真的情况下，则AB一定为真，故A + AB = A；

③消项法：AB + A'C + BC = AB + A'C ,AB + A'C + BCD = AB + A'C

    例：

 

Y1 = AC + AB' + (B + C)' = AC + AB' + B'C' = AC + B'C';
Y2 = AB'CD' + (AB')'E + A'CD'E = AB'CD' + (AB')'E;
Y3 = A'B'C + ABC + A'BD' + AB'D' + A'BCD' + BCD'E'
   = C(A^B)' + D'(A^B) + CD'(B(A' + E')) = C(A^B)' + D'(A^B);

 

    注意出题的时候，不一定按照常规的公式来出，有可能换着字母出题，让人觉得不适应。第一个公式和第二个公式之间，很明显暗含了一个吸收法的公式，因为BC所表示的范围要比BCD大，所以第一个公式成立的话，那么第二个公式一定成立。

④消因子法：A + A'B = A + B;

    例：

 

Y1 = B' + ABC = B' + AC;
Y2 = AB' + B + A'B = B + A + A'B = A + B;
Y3 = AC + A'D + C'D = AC + (A' + C')D = AC + (AC)'D = AC + D;

 

⑤配项法：

    1.根据基本公式：A + A = A；所以，逻辑函数中重复写入某一项，有时能够获得更加简单的化简结果。

 

Y = A'BC' + A'BC + ABC;重复写入A'BC
所以：Y = (A'BC' + A'BC) + (A'BC + ABC) = A'B + BC;

 

    2.根据基本公式A + A'=1；所以，可以在函数式中的某一项乘以(A+A')，然后拆分成两项分别与其他项合并，有时可以得到更加简单的结果。

    例：

 

Y = AB' + A'B + BC' + B'C
  = AB' + A'BC + A'BC' + BC' + AB'C + A'B'C
  = (AB' + AB'C) + (BC' + A'BC') + (A'BC + A'B'C)
  = AB' + BC' + A'C

 

二、卡诺图化简法

    卡诺图化简比较直观简单，一般可以用于公式法化简之后的验证！

三、考研真题解析

（2017山东大学考研906）用公式化简：F=AD+BCD'+(A'+B')C

【解析】

    常规想法：

 

F = AD + BCD' + A'C + B'C
  = AD + C(B' + BD') + A'c
  = AD + C(B' + D') + A'C
  = AD + C(A' + B' + D')
  ……

 

    好像做不动了，怎么去解决这个问题呢？

    用卡诺图！

    虽然题目中，明确规定使用公式法化简，但是此处想不到用什么公式怎么办，那就从卡诺图入手，看看是否有突破口，然后反推公式法化简。

    卡诺图如下：

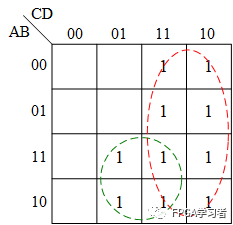
    可以得出最后的结果是：AD + C;

    怎么由这个结果往回推呢？

    首先：前面得到F = AD + BCD' + A'C + B'C

 

F = AD + BCD' + A'C + B'C    //式子中已经有AD，暂时不用处理

 

    在卡诺图中，除去AD的部分，再把其余表达式在卡诺图中标出来，可以看到，剩余的部分无论怎样都无法构成C，少了一项ABCD：

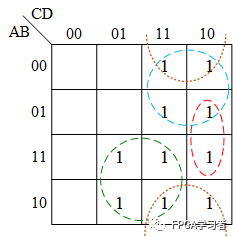
    所以，需要从AD（绿圈）中分出一部分来，即下图中粗长方形圈的部分：

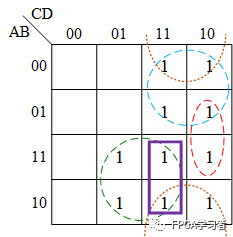
    这便相当于在原有的表达式中添加了一项：ACD

    即：

 

F = AD + BCD' + A'C + B'C
  = AD + ACD + BCD' + A'C + B'C
  = AD + C(A' + AD) + C(B' + BD')
  = AD + C(A' + D) + C(B' +  D')
  = AD + A'C + CD + B'C + CD'
  = AD + C(D' + D) + A'C + B'C
  = AD + C + A'C + B'C
  = AD + C

 

【总结】

    上题旨在分析添加某一项的思想。

    添加某一项来帮助化简，本身就是一个比较难想出来的过程；通过卡诺图画图分析的形式，可以帮助我们理解为什么要添加某一项。并且，这样做也可以在遇到困难的题目，实在解决不了时，当成一个急救的办法。

 

 

　　审核编辑：汤梓红