

基于变换光学的超散射的发展历程
EMC/EMI设计
描述
|作者:陈焕阳1,† 段琦琳1 伍瑞新2 马红孺3
(1 厦门大学物理科学与技术学院)
(2 南京大学电子科学与工程学院)
(3 云南大学物理与天文学院)
本文选自《物理》2022年第12期
摘要 基于变换光学的幻象光学器件能够表现出自然界中不存在的现象,如隐身、超散射和隐形门等。其中电磁超散射现象利用变换光学中的折叠几何变换,使得物体的散射截面远大于其几何截面,颠覆了人们对于传统散射中散射截面通常小于散射体几何截面的认知。这一现象也为现实中实现“穿墙术”提供了可能。文章着重介绍了基于变换光学的超散射的发展历程以及利用超散射实现隐形门的方法。隐形门在自由空间的实现为将来幻象器件的设计提供了新的思路。
1 引言
许多影视和文学作品中对于“隐身”的描绘令人心驰神往,其中最著名的当属《哈利波特》中的隐身衣,当披上隐身衣即不为外部所见。人能感知到物体是由于接收到了物体反射的光,因此隐身的关键就是对于光的操纵。穿墙术在神话中指人作为主体具有穿过实体墙的超能力,现实中“穿墙”则需要通过改变墙的特殊光学性质来实现。对电磁波来说,穿墙术就是物体可以穿过一道特殊的门,而此门却不为观察者所见,即“隐形门”。用隐形门实现的穿墙术与幻象光学息息相关。物体的幻象光学效应是指被观测到的物体和实际物体本身不同的一种光学现象,其中一个典型的例子是超散射效应,散射体的散射截面被极度增大[1],即对观察者而言物体的尺寸变得很大。2009年,上海交通大学马红孺/罗旭东课题组在研究中首先发现超散射。理论研究表明,超散射体可以用补偿介质[2]结合变换光学的方法[3]加以实现。这一方法已被用来设计许多奇妙有趣的幻象光学器件,如基于超散射效应的隐形通道或隐形门[4]、超吸收体[5]、非包裹隐身衣[6]和内窥镜[7]等,其中隐形门是最受关注的幻象光学器件。通过合理设计材料的介电常数ε 和磁导率μ (或折射率n ),2009年研究人员首先在理论上实现了隐形门。然而,此隐形门对所需材料的折射率分布要求极其苛刻[4],在实验上很难实现。后来人们提出一种基于简化参数的隐形门设计方案[8],并用电路等效的方法验证了隐形门的存在性[9]。然而直至2021年,真正的隐形门才在实验上得到证实。南京大学伍瑞新课题组和陈焕阳合作,首次在微波频率的自由空间中验证了超散射现象,在实验中实现了电磁隐形门这一幻象光学器件[10]。
隐形门从首次的理论提出到最终的实验实现经历了十余年。本文将着重介绍隐形门的发展历程,主要从三个方面概述:首先是变换光学这一强有力理论的提出;其次是从准静态极限到电磁超散射的提出;最后是基于超散射效应的隐形门理论设计以及实验验证。隐形门在实验上的成功实现将为今后新型光场调控器件的应用和发展提供新的思路。
2 变换光学
光线在均匀介质中沿直线传播,当光线通过两个介质的交界面时会发生偏折。在生活中,放在盛有水的透明杯中的筷子仿佛被“折断”就是这一原理的体现。当折射率出现渐变分布时,比如由于温度的不均匀导致沙漠上空气的密度不同从而产生渐变的折射率分布,进而出现神奇的海市蜃楼现象。这让我们不禁想到,只要设计出具有一定折射率分布的介质,那么光线就会在其中沿着特定的方向传播。
2006年,Pendry等[3]和Leonhardt[11]分别独立地提出了通过变换光学设计隐身衣的方法。如图1(a)所示,在“虚拟空间”,即真空中,光线沿着直线传播,通过坐标变换,空间中的一个点膨胀开形成一个“物理空间”中的圆(图1(b)),光线会绕着红色圆圈传播,因此红色圆圈内部对外部不可见,呈现出隐形效果[12]。这一理论的提出让《哈利波特》中神奇的隐身衣有了实现的可能。随后,Smith等人利用开口谐振环作为超构材料的结构单元在微波波段的实验上实现了单频的二维隐身器件[13]。自此,变换光学因具有可自由操控光场的能力吸引了人们的广泛关注。
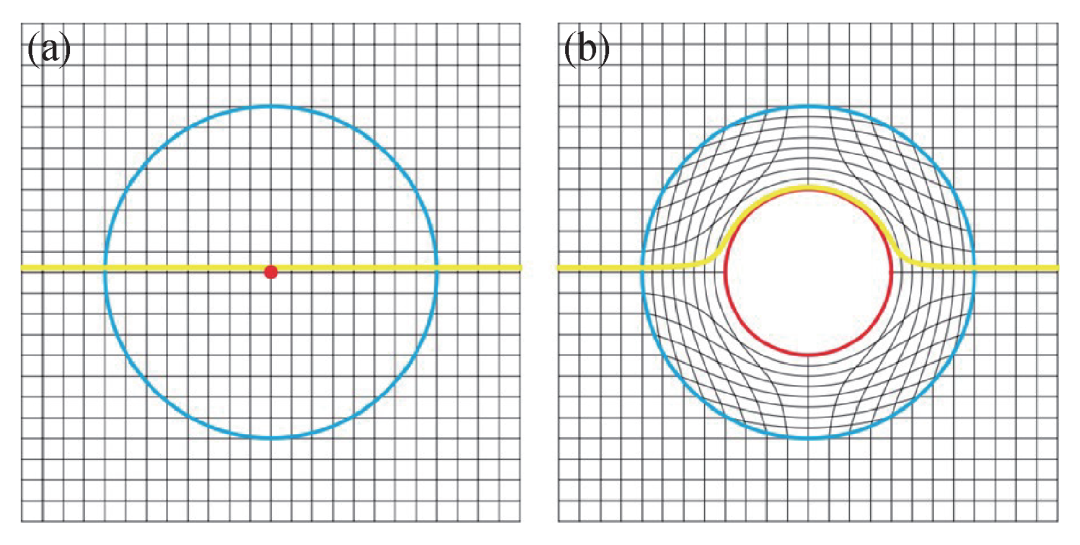
图1 坐标变换 (a)变换前在自由空间沿直线传播的光线;(b)通过变换将一个点膨胀成一个圆(红色圆圈),光线绕过圆形区域传播[12]
变换光学的核心是通过坐标变换在两个空间(虚拟空间和物理空间)建立起变换关系。由于坐标变换前后麦克斯韦方程组具有形式不变性,故两个空间中的电磁参数(介电常数ε和磁导率μ)可以建立起与坐标变换的对应关系[14]:
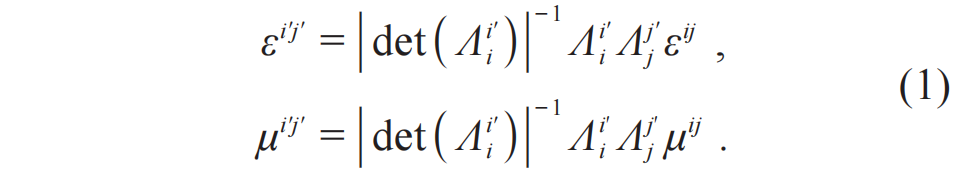
其中
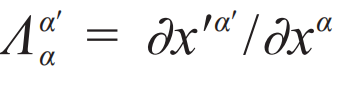
是虚拟空间与物理空间的雅可比变换矩阵,i、j 以及i '、j '从1到3选值以分别表示三个空间坐标。利用变换光学可以设计出许多具有新颖功能的器件,如隐身衣[15]、旋转衣[16,17]、汇聚器[18]以及幻象器件等。

图2 部分幻象光学器件及其对应的坐标变换关系 (a)理想隐身衣;(b)弱化设计后的隐身衣;(c)基于法布里—珀罗共振的隐身衣;(d)折叠变换后的隐身器件;(e—h)相应器件对应虚拟空间r与物理空间r ′的变换关系,其中黄色圆点对应变换的转变点,r与r ′分别表示变换前后同心圆环的半径
变换光学自提出以来,最受关注的就是“隐身衣”的设计,如图2(a)所示,隐身衣可以引导光线围绕物体传播,从而使物体“隐形”。在圆柱极坐标下,该理想二维隐身衣对应的变换关系如图2(e)所示,即:
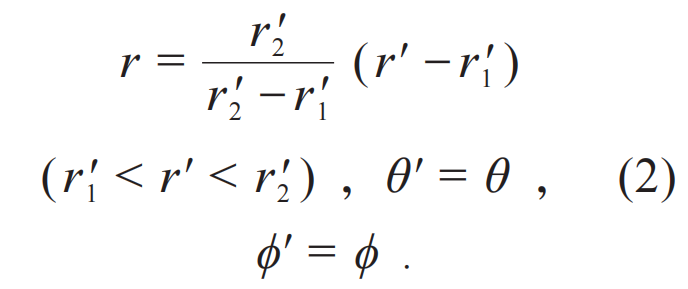
然而这样的理想隐身衣只能在单一的频点下工作,无法在较宽的频率范围内实现完美的隐身效果。针对这一问题,陈焕阳等提出了色散隐身衣[19],这种隐身衣相较于理想隐身衣工作频率有所拓宽,但伴随着部分性能的牺牲。色散隐身衣设计的核心思想是用一个更一般的变换形式,如图2(f)所示,将一个共心圆环区域区域r0 < r ≤ r2′压缩成为另一个共心圆环区域r1′ < r ≤ r2′,当r0 = 0时,该变换就回到理想的隐身衣情况。这样的隐身衣是弱化设计后的隐身衣,如图2(b)所示,该弱化隐身衣相当于自由空间内存在一个半径为r0的微小散射体。因此图2(f)对应的坐标变换的转变点,即在虚拟空间中的r1,相较于图2(e)有所抬高。
2015年,陈焕阳/侯波课题组将法布里—珀罗共振引入了变换光学器件的设计中[20],这样的器件可以在多个共振频率下工作,使得变换光学器件的多频率应用成为可能。如图2(g)所示,其变换的核心是将虚拟空间中的r1 ≤ r < r2映射到了物理空间的同心圆柱层r1′ ≤ r < r2′,当r2′ = r2且r1′ < r1时,这一变换就对应波的隐身汇聚器件。当r1趋近于r2时,对应极端版本的隐身汇聚器件。更进一步地,当r1′ ≤ r < r2′时,令εr = ∞,εθ = εθ(r ′)且μz = 1(横磁模式对应磁场沿着z方向),其中εr 和εθ 对应r 方向和θ 方向的介电常数分量,μz对应z 方向的磁导率分量;而当0 ≤ r ′ < r1′时,令ε = (r2′/r1′)2,μz = 1,则这个器件为法布里—珀罗共振的隐身汇聚器件,其r方向的法布里—珀罗共振条件可写为
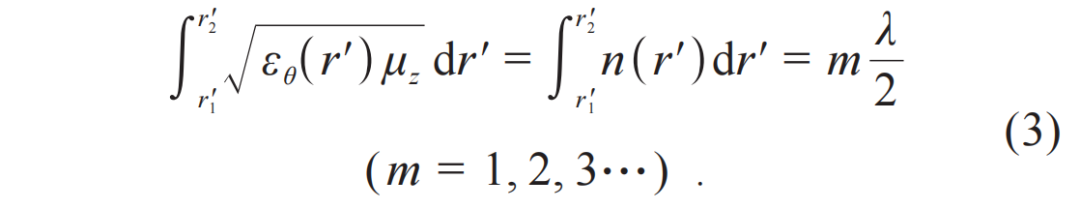
当m = 3,r2′ = 2,r1′ = 1时,εθ(r′) = (3 - r ′)2,其电磁波分布如图2(c)所示,并且这一器件在实验上得到了验证。
当变换选择的标记点位置进一步抬高,则对应折叠几何变换。与之前提到的三种变换不同的是,如图2(h)所示的折叠变换由于斜率为负将会引入负折射率材料(ε<0,μ<0)[21,22]。负折射率材料在自然界中并不存在,但是可以通过人工超构材料构造出ε 和μ 同时为负的负折射率材料[23,24]。在负折射率材料中,光的传播与其在传统材料中的传播特性相反,从而引发许多“违背常理”的光学现象,为人们操控光的传播提供了更多的可能。其中最著名的应用是Pendry提出的可以实现超越衍射极限的完美成像效果[22]。这一成像过程在几何光学方面,可以从变换光学的角度来看,将其理解为空间的折叠变换,由虚拟空间中的单个点对应于物理空间中的三个点[25]。早在2003年,Pendry基于负折射率平板提出了补偿介质的概念[2],补偿介质由两个具有相反电磁特性的区域构成,光在通过补偿介质后没有相位的积累,看起来仿佛这一块区域不存在[26]。在图2(d)中,由内向外三个圆的材料依次是均匀介质(r < r1′)、负折射率材料(r1′ < r < r2′)和空气(r2′ < r < r3′),空气层和负折射率层构成了补偿介质,即在区域(r1′ < r < r3′)之间形成了光学空洞,光线传播后没有相位的积累。这一系统的散射特性主要取决于放置在核层的物体[26]。
结合负折射率和补偿介质还可以设计出许多有趣的幻象光学器件。赖耘等人提出了非包裹式的隐身[6],其原理是利用补偿介质来消除被隐物体的反射以实现隐身效果。这不同于图2(a)中的隐身装置,由于光线无法进入r = r1′内部,故图2(a)中隐身装置内部的观测者是看不到外部情况的,而非包裹式隐身内部的观测者可以看到外部情况。通过折叠几何变换还可以设计出反隐身的器件,破坏由正折射率材料组成的隐身器件的隐身效果[27]。这些神奇的幻象器件不禁让人思考,所见即是真实吗?
3 电磁超散射的提出与发展
电磁波入射到物体表面时会发生散射,电磁散射是非常普遍的物理现象[28]。例如,晴朗的天空呈现蓝色源于瑞利散射:空气中的分子尺寸远小于光的波长,可见光中蓝光波长较短因此更容易发生散射,这就是蔚蓝天空所蕴含的物理奥妙。当空气中存在较多比光波长尺寸大的尘粒和液滴时会发生米氏散射,米氏散射中所有波长的光均等散射,故而天空呈灰白色。电磁散射还具有许多重要的应用。例如,在通信领域中,可以利用对流层对电磁波产生的散射作用进行超视距通信;在军事雷达探测中,通过分析散射特征可以得到散射物体的信息。
可以看到在传统散射中,散射特征与散射体尺寸息息相关,物体的散射截面通常小于其几何截面。普通材料对于电磁波的调控能力有限,即便是相较于波长尺寸较大的散射体,其散射截面仅趋近几何截面。一些基于共振效应获得的超出几何截面的散射截面,也可以通过分析各级米氏散射系数,将其与非共振散射体区分出来。变换光学和超材料的出现,极大增强了人们对电磁场的操控能力,除了可以完美消除散射的隐身效应,还可以使小物体与大物体的散射特征无法区分,即“超散射”现象。这一现象颠覆了电动力学中大尺度物体最大散射截面是其几何截面的传统认知。
超散射通过增强散射截面使得一个物体看起来比其实际尺寸大。该现象在传感[29]、汇聚能量[30,31]、荧光成像[32]、电力无线传输[33]等方面有广泛的应用前景。考虑从如图3(a)所示核层结构的散射问题出发,在准静态极限下(即物体尺寸远小于波长),可以使用近似的麦克斯韦方程组来求解问题,并且可以忽略其他项而只考虑偶极子项[34],分析芯层(ε1)、壳层(ε2)和背景材料(ε3)组成的物体对于以离散电偶极子为源的响应[35]。当ε1+ε2=0且ε2+ε3=0时,物体对于外部场没有影响;而仅当ε2+ε3=0时,芯层的散射会超过壳层的散射,仿佛芯层的半径被放大。在准静态极限下可以产生芯层被放大的现象,从准静态极限过渡到电磁散射(需要考虑其他阶数项的散射)。目前主要有三种方法可以实现超散射:第一种是通过变换光学的方法,并引入补偿介质的概念来放大物体,从而实现超散射[1];第二种是利用多层金属—介质亚波长纳米柱表面等离激元的共振打破单通道散射极限,以此实现超散射现象[36,37],该方法通过共振只能实现有限阶数的放大,并且材料的损耗对散射增强效果影响很大;第三种是利用近零折射率材料来增强物体散射[38,39],该方法需要近零折射率的背景环境,对制备和兼容性提出了进一步的挑战。本文聚焦于第一种实现超散射的方法,下面将做进一步的介绍。
在准静态条件下,低阶散射系数起到决定性作用,当物体的尺寸与波长可比拟时,不能忽略高阶散射,通过变换光学的手段可以实现具有与波长可比拟尺寸的物体的超散射[1]。从图3(b)的负折射率平板出发,在小于负折射率平板(黄色区域)厚度的位置放置点源S,通过几何光学可知点源S会在F2和F1处成像。在R1处设置完美电导体边界(PEC),光线会被反弹回来,而区域R2 < x < R1与区域R3 < x < R2构成一对补偿介质,R1处的完美电导体边界仿佛被移至R3处。再将该平板卷成一个圆柱,如图3(c)所示,利用图2(h)的坐标变换,同理,区域R1 < r < R2与区域R2 < r < R3构成了补偿介质,内部r = R1的完美电导体边界在视觉上被移至r = R3处,物体的几何尺寸被等效放大而实现超散射效果。图3(d)和3(e)为COMSOL仿真计算结果,其中黑色实线表示圆柱边界,黑色虚线表示散射增强后的等效区域。
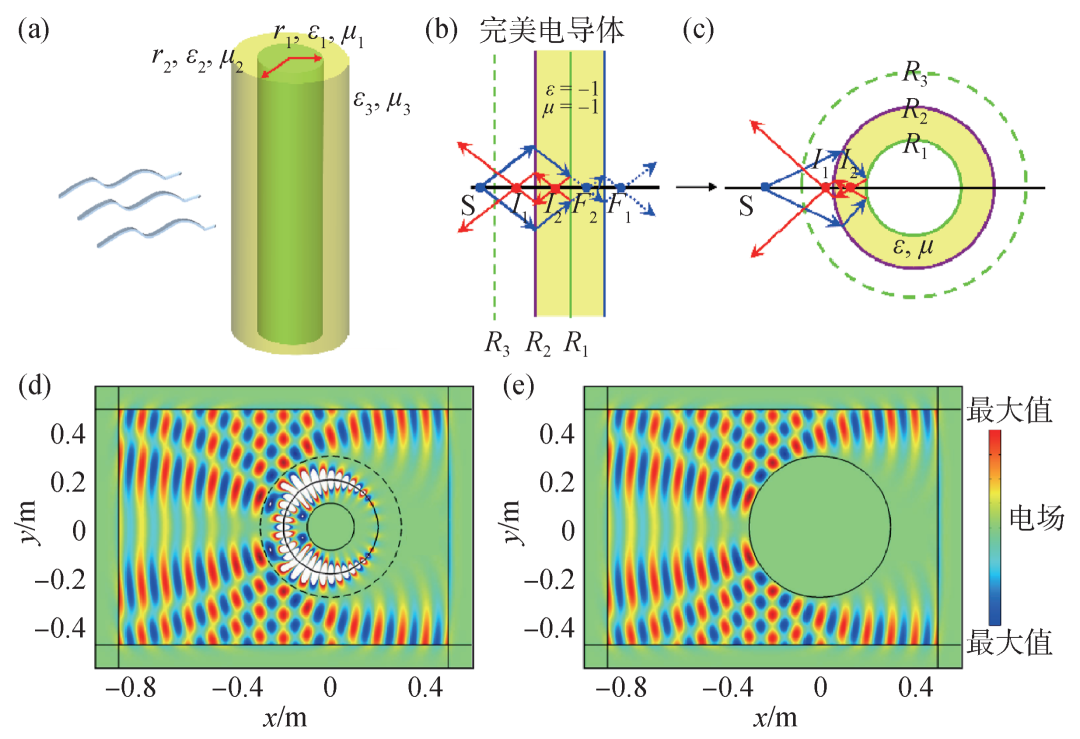
图3 (a)核层结构的电磁散射示意图;光线在平板负折射率材料(b)与圆柱负折射率材料(c)中的传播,其中绿色实线为完美电导体[1];(d)内外半径分别为R1=0.1 m与R2=0.2 m的超散射圆柱周围的总电场分布[1];(e)半径R3=0.3 m的完美电导体的总电场分布,(d),(e)均为平面波入射[1]
当频率为3 GHz的横电模式(电场沿着z方向)平面波入射时,图3(d),(e)的电场分布相同,证明了超散射现象。其背后的物理机制是负折射率壳层对于倏逝波的放大。这种超散射现象不仅可以放大圆柱形状的物体,也被证明了可以放大其他形状的物体[26,40]。
4 电磁隐形门的实现 在电影《哈利波特》中, 站台是登上霍格沃茨特快列车的隐形通道(或隐形门),如图4(a)所示,这既是魔法,也可以是一种幻象光学效应,即这个通道在空间上是实际存在的,但是在通道外的观察者却无法从视觉层面看到。随着变换光学的不断发展,研究人员发现结合超散射技术,便可实现隐形通道效应。
站台是登上霍格沃茨特快列车的隐形通道(或隐形门),如图4(a)所示,这既是魔法,也可以是一种幻象光学效应,即这个通道在空间上是实际存在的,但是在通道外的观察者却无法从视觉层面看到。随着变换光学的不断发展,研究人员发现结合超散射技术,便可实现隐形通道效应。
2009年,上海交通大学马红孺/罗旭东课题组[4]进一步发展了图3(d)中提出的超散射体,将其推广为方形超散射体并置于两个恰当距离的金属墙体之间。如图4(b)所示,其中完美电导体的高度为2b3,隐形通道的区域宽度设计为2a3。当|x| ≤ a3+δ区域不存在超散射体时,则此通道区域( |x| ≤ a3+δ )显然可以通过分析散射电磁波被探测到,而当在该通道区域中放置设计好的方形超散射体时(该超散射体为Γ2边界面包围的区域),由于该超散射体散射截面大于其几何截面,故电磁波无法通过,因此构造了一个“隐形”通道。他们利用COMSOL仿真展示了当入射光源位于隐形门一侧时,观察者在隐形通道两侧时会看到截然不同的“景象”,如图4(d),(e)所示。这样的隐形门设计虽与实际场景相符合,但实现起来需要负折射率材料,并且对材料的折射率分布要求苛刻,限制了隐形通道器件的发展。
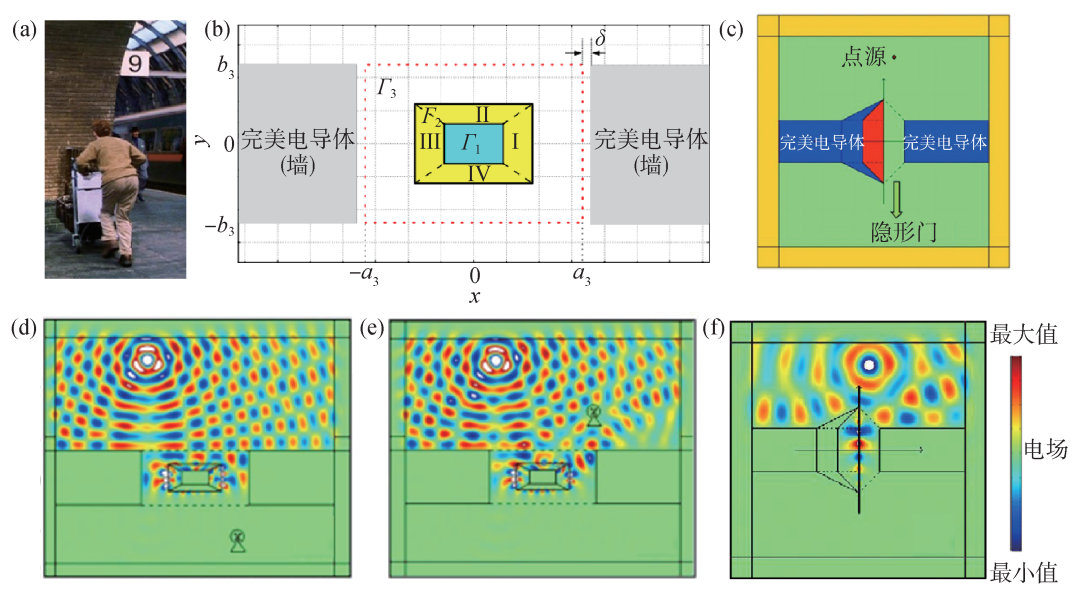
图4 隐形门的理论原型设计[4,8] (a)《哈利波特》中的 站台;(b)一种包裹式的隐形门,其中Γ1为完美电导体区域,Γ2为负折射率包裹区域,Γ3为电磁波无法透过的区域;(c)一种简单化的隐形门;(d),(e)对应(b)中的隐形门,通过仿真演示了观察者分别位于两侧的效果;(f)对应(c)中的隐形门效果
站台;(b)一种包裹式的隐形门,其中Γ1为完美电导体区域,Γ2为负折射率包裹区域,Γ3为电磁波无法透过的区域;(c)一种简单化的隐形门;(d),(e)对应(b)中的隐形门,通过仿真演示了观察者分别位于两侧的效果;(f)对应(c)中的隐形门效果
同年,陈焕阳等[8]提出一种简化的隐形门原型设计,如图4(c)所示。这种新的超散射体不再需要复杂折射率分布的材料,取而代之的是填充部分折射率为-1的材料,并且还具有一定的工作带宽。在光源激励下,由于负折射率材料的存在(图4(c)中的红色区域),会在空气和材料界面激发表面波,进而表现出超散射的现象,其散射截面等效于器件本身附加填充负折射率材料区域的镜像部分。在考虑横电模式的情况下,在超散射体两端放置完美电导体,自然形成了隐形通道。如图COMSOL仿真结果4(f)所示,一侧的电磁波在通过器件的空气通道时被完美“阻挡”,但却可以让物体通过,充当着完美的隐形门。此外,他们还给出了利用磁光子晶体来实现隐形门的方案,并进行了仿真验证。
在隐形门简易化原型提出后不久,研究者们便利用电路模拟方法在实验中予以实现。2010年,中国科学院电子学研究所李超和陈焕阳等人合作,利用传输线模型,在实验中首次模拟验证了隐形门器件[9]。如图5(a)所示,他们利用串联电感和并联电容来模拟空气,利用串联电容和并联电感来模拟负折射率材料,并优化两者的边界,最后在电路板上构造了隐形门器件,通过图5(b)的实验测量结果可以看出,隐形门可以完美阻挡交流信号的传播。
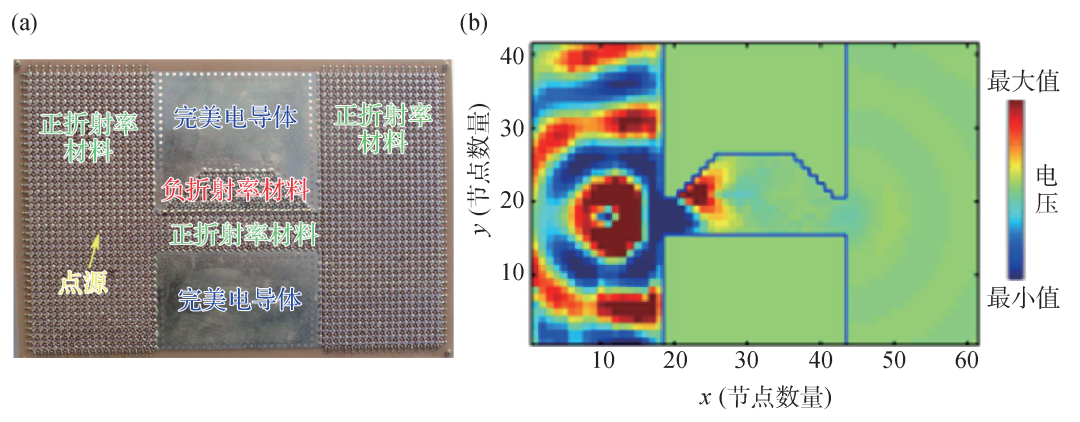
图5 隐形门的电路实验实现[9] (a)利用电路模型模拟的隐形门器件;(b)电路模拟隐形门实验测量结果
电路模拟的验证方法为幻象光学器件的实现提供了一个可行方案,然而这与真实的场景仍有天壤之别,人们期待在真实环境中实现真正的隐形门。直到2021年,南京大学伍瑞新课题组与陈焕阳合作[10],采用简化的隐形门设计方案[8],利用自偏置锶磁铁氧体阵列构建超散射体,并在自由空间中搭建了隐形门,如图6(a)所示。在实验中首次直接观测到空气通道对电磁场有着显著的阻断作用,如图6(b)所示,入射电磁波沿着通道迅速衰减,在空气通道的尽头电场几乎消失,从而实现了自由空间中真实的隐形门。作为对比,如图6(c)所示,置于两完美电导体之间与图6(c)具有相同宽度的空气通道则无法阻挡电磁波的传播,入射电磁波可以穿透空气通道而没有衰减。为了进一步说明该隐形门对电磁波的阻挡效果,图6(d)展示了在图6(a)中标记的从B点到B′点的归一化电场能量密度,可以看到在隐形门中,电场能量密度迅速衰减,从B点到B′点有90%的能量被阻挡,而在金属波导中电场能量密度的衰减仅为15%。图6(e)则展示了在实验中隐形门和金属波导两个端口的电场能量密度比值与频率的关系,可以看到在绿色阴影区间内比值逐渐减小而对应的金属波导的比值则较为稳定。综上说明了该隐形门对电磁波传播的阻挡能力。超构材料隐形门的实现进一步推动了幻象光学器件的发展,使得隐形门在真实场景中的应用成为可能。
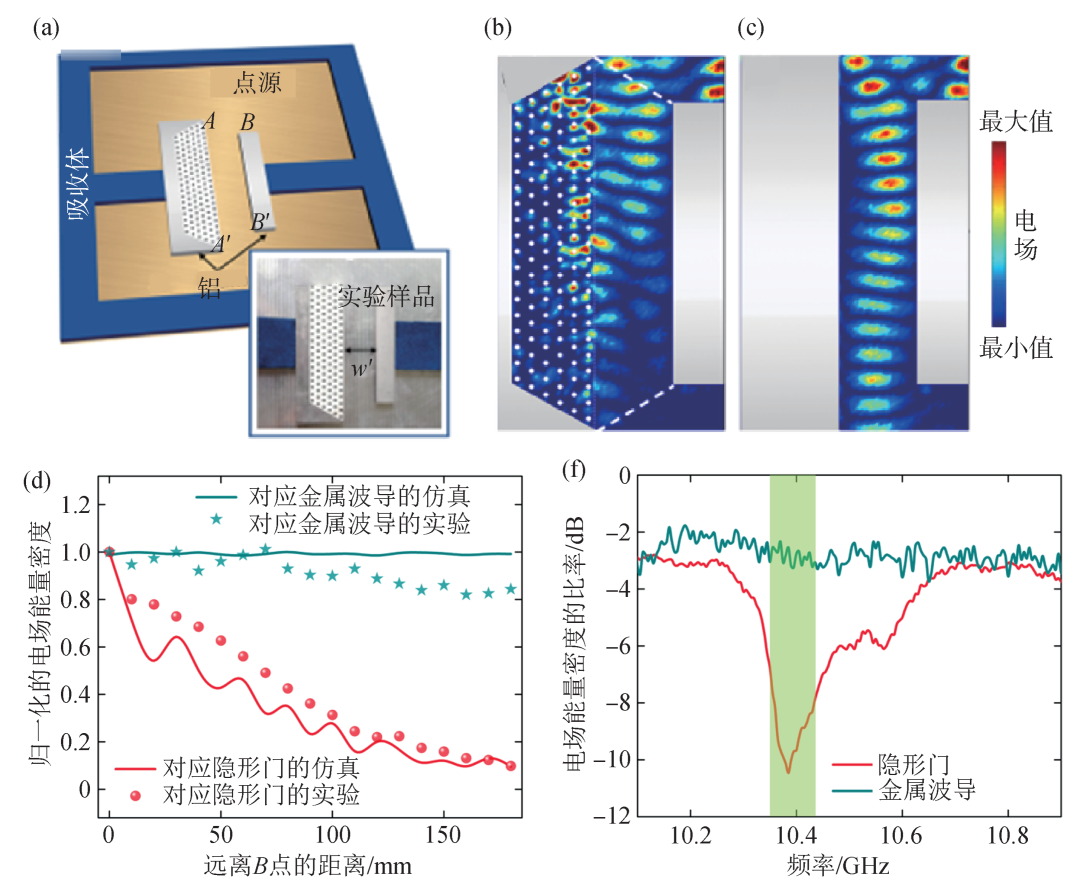
图6 隐形门在微波频段的自由空间的实验实现[10] (a)利用铁氧体阵列(白色梯形阵列区域)搭建的电磁隐形门器件,与铁氧体阵列接合的金属铝作为完美电导体;(b)电磁隐形门实验测量结果;(c)用完美电导体代替铁氧体阵列实验对比结果,在图(b),(c)中,铁氧体用白点标记,铝用灰色表示;(d)实验与仿真中沿着隐形门(对应(b)图)和金属波导(对应(c)图)的空气通道的归一化的电场能量密度;(g)实验中隐形门与金属波导在输出端口与输入端口处的电场能量密度比值与频率的关系
5 总结
一直以来,自由操控电磁波是人们孜孜不倦的追求。应用变换光学使得人们可以通过设计材料的电磁参数实现对电磁波散射的调控。当散射被抑制时可以实现完美的隐身衣,当散射被放大时就可以实现超散射现象。超散射不仅在传感、能量收集等领域有广阔的应用前景,而且还可以用于构造如隐形门等光学幻象器件。隐形门从最开始的电路等效实验到微波频段的自由空间中的实验实现,预示着幻象光学领域又前进了一大步。值得注意的是,由于材料参数的简化,该隐形门器件的横向和纵向电尺寸(物理尺寸/波长)无严格的限制(横向电尺寸通常大于1,纵向电尺寸通常大于2),并且可以拓宽到其他光学频段,例如可见光、红外波段等。然而目前隐形门的实现主要依赖负折射率材料(折射率n=-1),因此在工作带宽上存在一定的限制,且不能推广到几何光学领域。随着声学负折射率材料的提出,该隐形门今后有望推广到三维声学领域中用于声波的调控。
致 谢 有许多合作者都对这一系列工作做出了极大的贡献和影响,不能一一罗列。比如,香港科技大学的陈子亭教授,张昭庆教授和沈平教授,上海交通大学的罗旭东教授和宁夏大学的杨涛教授,南京大学的赖耘教授,苏州大学的侯波教授和徐亚东教授,南方科技大学的吴紫辉教授,复旦大学的林志方教授和浙江师范大学的刘士阳等,和他们在一起的讨论,是极其愉悦的回忆,也是人生的幸事!还要感谢厦门大学的博士生殷玉杭、赵鹏飞、朱杉的辛勤工作与校正。
参考文献
[1] Yang T,Chen H,Luo X et al. Opt. Express,2008,16:18545
[2] Pendry J B,Ramakrishna S A. J. Phys-Condens. Mat.,2003,15:6345
[3] Pendry J B,Schurig D,Smith D R. Science,2006,312:1780
[4] Luo X,Yang T,Gu Y et al. Appl. Phys. Lett.,2009,94:223513
[5] Ng J,Chen H,Chan C T. Opt. Lett.,2009,34:644
[6] Lai Y,Chen H,Zhang Z Q et al. Phys. Rev. Lett.,2009,102:093901
[7] Lai Y,Ng J,Chen H et al. Phys. Rev. Lett.,2009,102:253902
[8] Chen H,Chan C T,Liu S et al. New J. Phys.,2009,11:083012
[9] Li C,Meng X,Liu X et al. Phys. Rev. Lett.,2010,105:233906
[10] Ye K P,Pei W J,Sa Z H et al. Phys. Rev. Lett.,2021,126:227403
[11] Leonhardt U. Science,2006,312:1777
[12] Leonhardt U,Tyc T. Science,2009,323:110
[13] Schurig D,Mock J J,Justice B et al. Science,2006,314:977
[14] Pendry J B,Aubry A,Smith D et al. Science,2012,337:549
[15] Cummer S A,Popa B I,Schurig D et al. Phys. Rev. E,2006,74:036621
[16] Chen H,Chan C T. Appl. Phys. Lett.,2007,90:241105
[17] Chen H,Hou B,Chen S et al. Phys. Rev. Lett.,2009,102:183903
[18] Sadeghi M M,Xu L,Nadgaran H et al. Sci. Rep.,2015,5:1
[19] Chen H,Liang Z,Yao P et al. Phys. Rev. B,2007,76:241104
[20] Sadeghi M,Li S,Xu L et al. Sci. Rep.,2015,5:1
[21] Veselago V G. Sov. Phys. Usp.,1968,10:509
[22] Pendry J B,Phys. Rev. Lett.,2000,85:3966
[23] Smith D R,Pendry J B,Wiltshire M C. Science,2004,305:788
[24] Shalaev V M. Nat. Photon.,2007,1:41
[25] Leonhardt U,Philbin T G. New J. Phys.,2006,8:247
[26] Chen H,Chan C T,Sheng P. Nat. Mater.,2010,9:387
[27] Chen H,Luo X,Ma H et al. Opt. Express,2008,16:14603
[28] Kerker M. The Scattering of Light. New York:Academic press,1969
[29] Wan W,Zheng W,Chen Y et al. Nanoscale,2014,6:9093
[30] Schuller J A,Barnard E S,Cai W et al. Nat. Mater.,2010,9:193
[31] Green M A,Pillai S. Nat. Photon.,2012,6:130
[32] Kinkhabwala A,Yu Z,Fan S et al. Nat. Photon.,2009,3:654
[33] Zhu L,Luo X,Ma H. Appl. Phys. Lett.,2016,109:024103
[34] Alù A,Engheta N. J. Nanophotonics,2010,4:041590
[35] Nicorovici N,McPhedran R C,Milton G W. Phys. Rev. B,1994,49:8479
[36] Ruan Z,Fan S. Phys. Rev. Lett.,2010,105:013901
[37] Qian C,Yang Y,Xiong X et al. Phys. Rev. Lett.,2019,122:063901
[38] Zhou M,Shi L,Zi J et al. Phys. Rev. Lett.,2015,115:023903
[39] Zhou M,Ying L,Lu L et al. Nat. Commun.,2017,8:1388
[40] Pendry J B. Nature,2009,460:579
编辑:黄飞
-
散射体的光学手性响应2025-01-11 701
-
JCMsuite应用:散射体的光学手性响应2024-12-18 659
-
直径测量工具的发展历程2024-10-10 2039
-
NAND闪存的发展历程2024-08-10 3329
-
软件定义超构光学元件未来发展方向2023-10-16 992
-
光学表面的散射测量方法发展的趋势2023-09-08 2775
-
扬尘监测仪监测原理-激光散射 光学原理2023-05-27 1015
-
嵌入式系统发展历程是什么2021-12-22 719
-
压电MEMS微镜与光学超表面聚集,实现动态光束操纵2021-06-29 3784
-
DDR SDRAM的内存发展历程2021-01-06 2128
-
汇编语言的发展历程和特点2020-10-22 1947
-
新型超材料的发展前景怎么样2019-05-28 4129
-
纠正几点对散射屏幕的认识2010-02-11 2216
全部0条评论

快来发表一下你的评论吧 !

