基于PI双闭环解耦控制的三相SVPWM电压型逆变器(1)--数学模型

最近在研究三相逆变，写篇博客分享一下。

电路拓扑

如下图所示，为三相电压型逆变电路的主电路拓扑。主电路主要由四部分组成，直流电源、6个开关管（互补导通）、三个滤波电感和滤波电容组成的滤波电路、负载，实际上是三个星接的电阻。

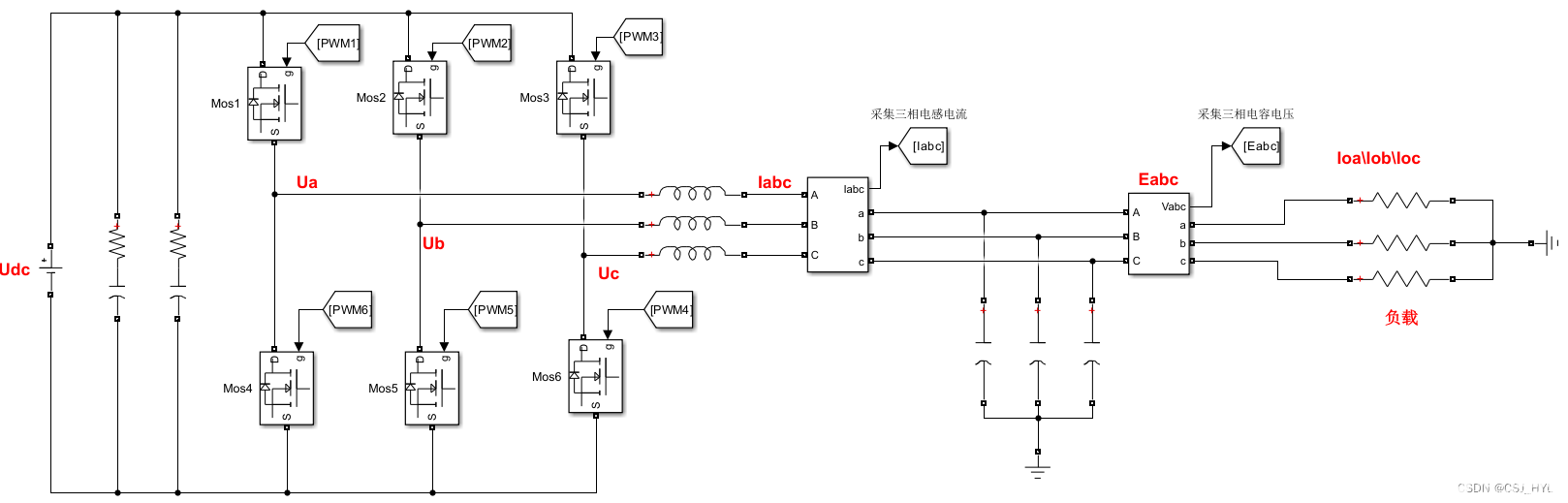
其中Udc表示直流侧电压，靠近直流侧的两个电容为输入滤波电容，Ua、Ub、Uc表示为每个逆变桥臂的中点到直流测电压负极，是逆变桥臂输出的每相脉冲电压，Ia、Ib、Ic表示为三个流经滤波电感的相电流，Ea、Eb、Ec表示为电容电压，也就是负载电压。Ioa、Iob、Ioc表示为流经负载的电流。

逆变器的数学模型

需要通过建立逆变器的数学模型来研究该电路，为下一步设计控制器打好基础。分析这种电路，往往从电感、电容入手，根据KVL、KCL列写电路方程，进而得到电路的数学模型。

2.1 逆变器在三相静止坐标系下的数学模型

根据KVL定理，可列出副边abc三相的电压回路方程，公式（2.1）：

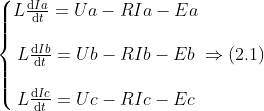
式中，R为相应回路电感的等效阻值，Ua、Uc、Uc分别为a、b、c三相的相电压，Ia、Ib、Ic为流经电感的电流。

根据KCL定理，可以得出副边电流的回路方程，公式（2.2）

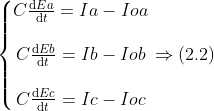
通过公式（2.1）、公式（2.2），我们就得到了该逆变器在三相静止坐标系下的数学模型。三相静止坐标系abc下的数学模型虽然能够很好地买描述电压和电流之间的关系，但是模型中有多个输入、多个输出，表达式和变量比较多，难以设计相应的控制器。

2.2 逆变器在αβ轴坐标系下的数学模型

通过Clack变换可以将模型简化，得到αβ正交坐标系下的表达式。原理如下图所示：

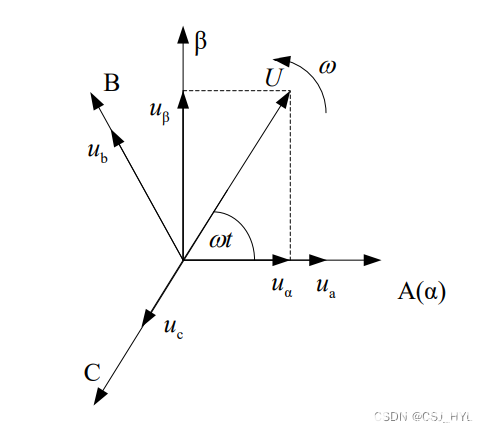
因为 Δ/Yo 变压器的存在使原边线电压和为零，所以原边不存在零序分 量，负载不平衡时作为扰动考虑，因此暂不考虑零轴，对应的变换关系为

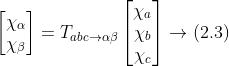
式中，变换矩阵

 

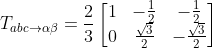
编辑。乘以2/3是因为做的是等电压的变换，原以是合成后的αβ轴的分量最大值是abc静止坐标系的3/2倍。还有一种变换类型是等功率的变换，这里不做讲述。

将式（2.1）、（2.2）、（2.3）联立，可以得出对应在αβ坐标系的方程，式（2.4）

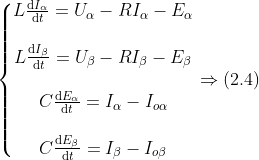
经过Clack变换后，减少了控制变量，简化了控制系统。并且αβ分量相互独立，没有耦合在一起，控制起来比较方便。但是传统的PI控制器对于追踪交流量效果并不好，会有静态误差产生。但对于直流量并不会产生静态误差，所以说还要进行Pack变换，将式（2.4）转换到dq坐标系下。

2.3 逆变器在dq轴坐标系下的数学模型

将两相静止αβ 坐标系中的变量变换到两相旋转 dq 坐标系中称为 Park 变换，其原理如下图所示。

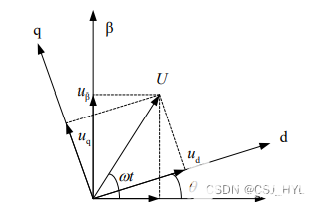
定义Park变换矩阵为，Cpark可以得到如下式(2.5)所示的关系。

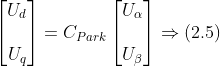
中,变换矩阵

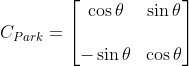
通过联立式(2.4)、(2.5)可以得到对应在dq轴坐标系下的数学模型，表达式为：

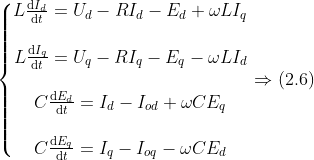
通过 Park 变换可将数学模型转换到旋转坐标系下。因为坐标系与参考旋转矢量的旋转的方向还有速度是相同的，所以它们两个是相对静止，在旋转坐标系下为直流量， 能够简化数学模型，使控制更容易实现。

3.逆变器的等效电路模型

在张兴的《PWM整流器》这本书中写到了这种等效变压器模型电路。

 

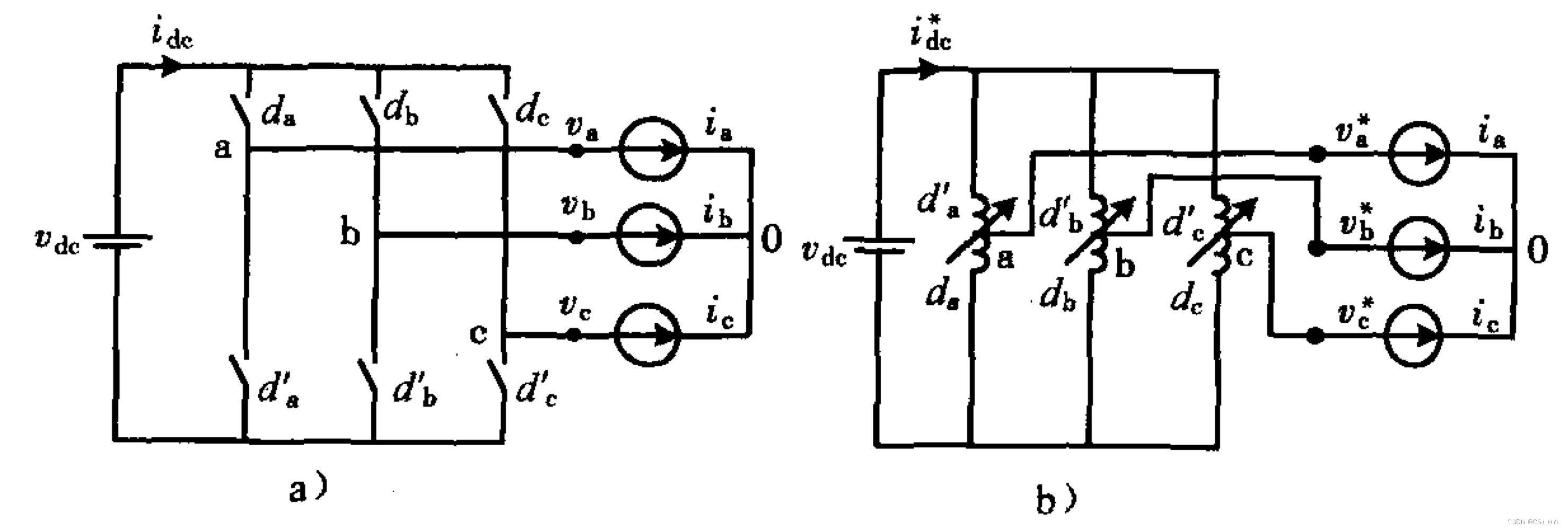
这里的da、db、dc、da'、db'、dc'表示的是对应开关管的PWM占空比，可以用自耦变压器来代替开关管，进而得出变压器模型 。

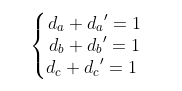
通过前面得出的dq坐标系下的数学模型，进一步可以得到dq坐标系下的变压器模型。通过这种模型可以帮助我们更好的去理解dq坐标系下的数学模型。

 

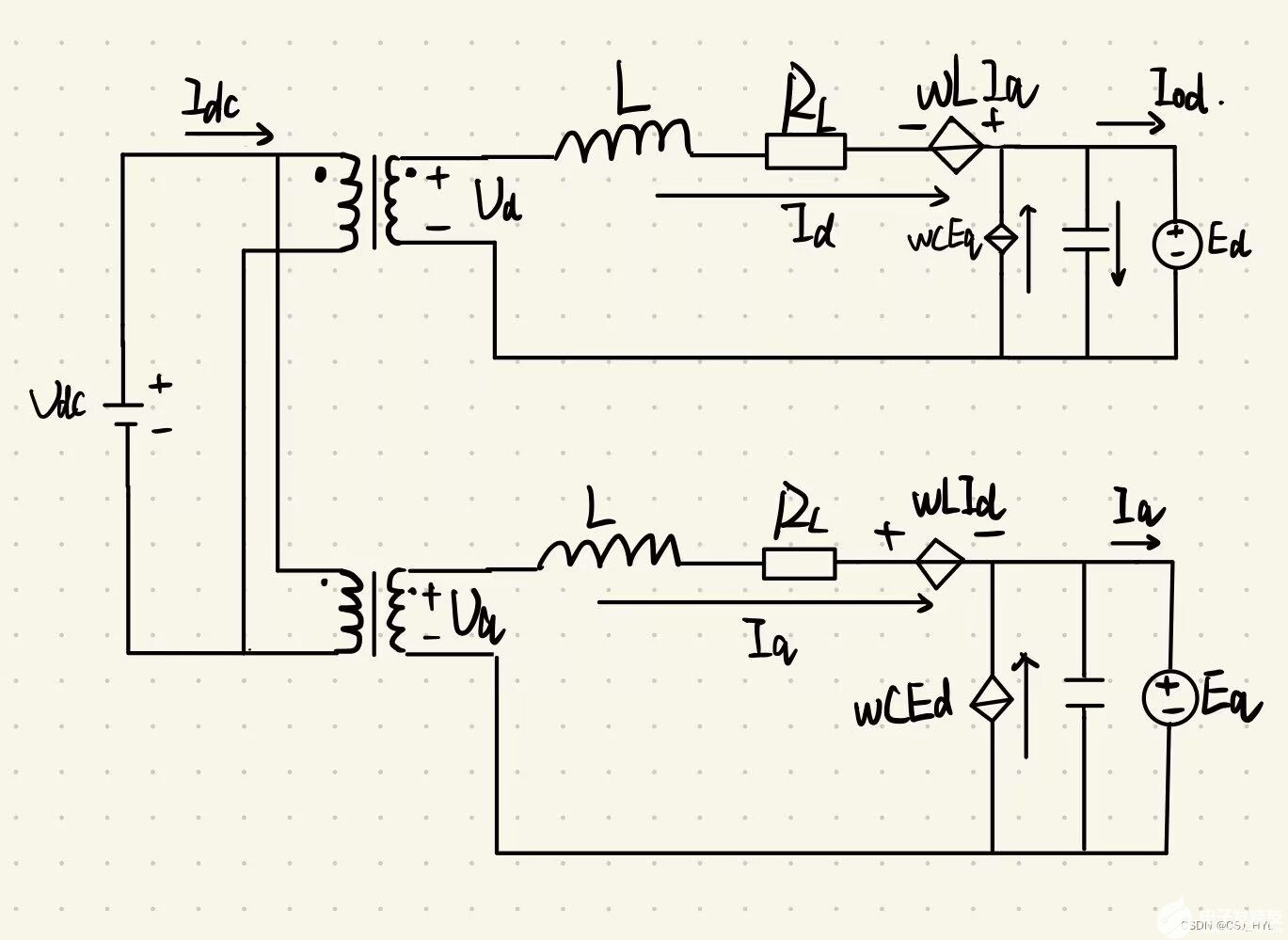
图画的不是太好

4.小结

通过以上变换得到了逆变器在不同坐标系下的数学模型，为控制器的设计打下了良好的基础。实际上控制器是按照dq坐标系下建立数学模型。

这里在建立数学模型的时候并没有去考虑调制的方法，实际上调制的方法是用来产生Ua，Ub、Uc的，完成建立数学模型并且完成设计控制器，我们就能得到目标的Ua，Ub、Uc，然后根据目标的Ua，Ub、Uc去调制，输出PWM，来产生原边电压，进而达到我们的控制要求。

还有一点就是这里的变换是通过矩阵的形式，在坐标系转换的运算过程中也是通过矩阵运算来实现的。

例如：

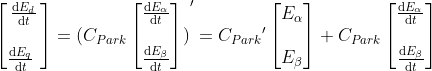
其中，

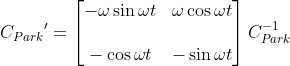
审核编辑：汤梓红