

MEMS振动监测:从加速度到速度
描述
MEMS加速度计终于达到了能够在各种机器平台上测量振动的程度。MEMS加速度计在功能方面的最新进展,以及MEMS加速度计相对于传统振动传感器(尺寸、重量、成本、抗冲击性、易用性)的诸多优势,正在推动MEMS加速度计在新兴的状态监控(CBM)系统中使用。因此,许多CBM系统架构师、开发人员甚至他们的客户都是第一次考虑这些类型的传感器。很多时候,他们面临着快速学习如何评估MEMS加速度计的能力以测量其机器平台上最重要的振动属性的问题。乍一看,这似乎很困难,因为MEMS加速度计数据手册通常用这些开发人员可能不熟悉的术语来表达最重要的性能属性。例如,许多人熟悉用线速度(mm/s)来量化振动,而大多数MEMS加速度计数据手册则以重力参考加速度(g)来表示其性能指标。幸运的是,有一些简单的技术可以进行从加速度到速度的转换,并估计关键加速度计行为(频率响应、测量范围、噪声密度)对重要系统级标准(带宽、平坦度、峰值振动、分辨率)的影响。
基本振动属性
这个过程从从惯性运动的角度回顾线性振动开始。在这种情况下,振动是一种平均位移为零的机械振荡。对于那些不希望他们的机器在工厂车间移动的人来说,零平均位移非常重要!振动传感节点中核心传感器的值将直接关系到它如何代表机器振动的最重要属性。为了开始评估特定MEMS加速度计的这种能力,从惯性运动的角度开始对振动有一个基本的了解是很重要的。图1提供了振动运动曲线的物理图示,其中灰色框表示中间点,蓝色图像表示一个方向的峰值位移,红色图像表示另一个方向的峰值位移。公式1提供了一个数学模型,描述了矩形物体在一个频率(fV),星等为 A有效值.
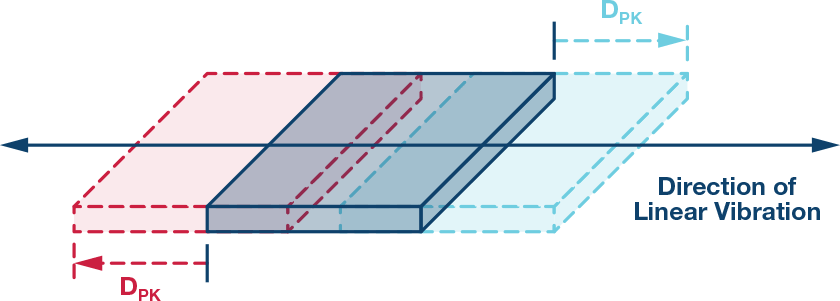
图1.简单的线性振动运动。
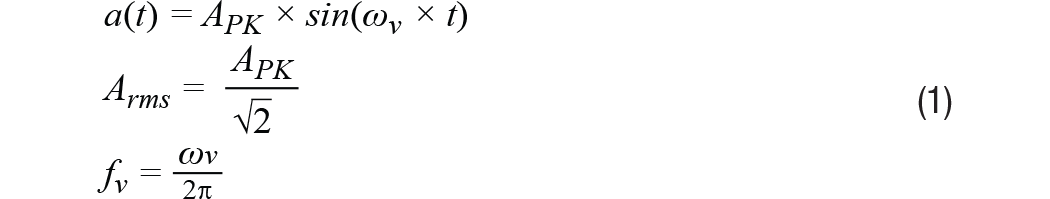
在大多数CBM应用中,机器平台上的振动通常比公式1中的模型具有更复杂的频谱特征,但该模型在发现过程中提供了一个很好的起点,因为它确定了CBM系统经常跟踪的两个常见振动属性:幅度和频率。这种方法在将关键行为转换为线速度方面也很有用(稍后会详细介绍)。图2提供了两种不同类型的振动曲线的频谱图。第一个轮廓(参见图2中的蓝线)在其频率范围内具有恒定的幅度,介于f1和 f6.第二个轮廓(见图2中的绿线)在四个不同频率下具有峰:f2, f3, f4,和 f5.
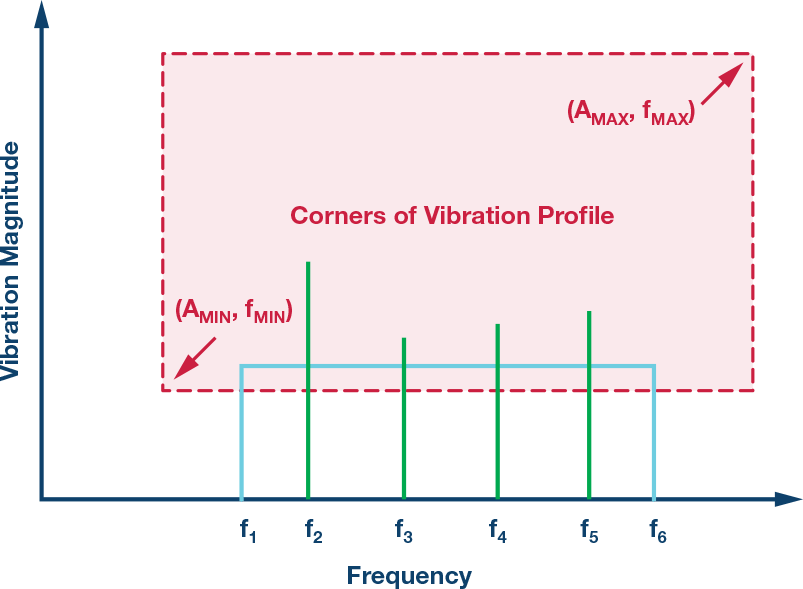
图2.CM振动曲线示例。
系统要求
测量范围、频率范围(带宽)和分辨率是三个常见属性,通常量化振动检测节点的能力。图 2 中的红色虚线通过一个受最小频率 (f ) 约束的矩形框来说明这些属性最低)、最大频率 (f.MAX)、最小星等 (A最低)和最大星等(A.MAX).在考虑将MEMS加速度计作为振动检测节点中的核心传感器时,系统架构师可能希望在设计周期的早期分析其频率响应、测量范围和噪声行为。有一些简单的技术可以评估这些加速度计行为中的每一个,以预测加速度计对给定要求的适用性。显然,系统架构师最终需要通过实际验证和鉴定来验证这些估计值,但即使是这些努力也会重视早期分析和预测加速度计功能的期望。
频率响应
公式2给出了一个简单的一阶模型,描述了MEMS加速度计在时域中对线性加速度(a)的响应(y)。在这种关系中,偏差(b)表示传感器在经历零线性振动(或任何类型的线性加速度)时输出的值。比例因子 (K一个) 表示 MEMS 加速度计响应 (y) 相对于线性加速度 (a) 的变化量。

传感器的频率响应描述了比例因子 (K一个),关于频率。在MEMS加速度计中,频率响应有两个主要因素:(1)其机械结构的响应和(2)信号链中滤波的响应。公式3给出了一个通用的二阶模型,该模型给出了MEMS加速度计对频率响应的机械部分的近似值。在此模型中,fO表示谐振频率,Q表示品质因数。
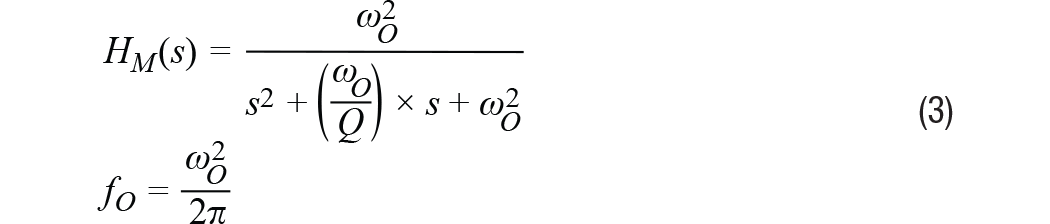
信号链的贡献通常取决于应用所需的滤波。一些MEMS加速度计使用单极点低通滤波器来帮助降低谐振频率下的响应增益。公式4提供了与此类滤波器相关的频率响应的通用模型(H南卡罗来纳州).在这种类型的滤波器模型中,截止频率(fC) 表示输出信号幅度比其输入信号低 √2 倍的频率。

公式5结合了机械结构(HM)和信号链(H南卡罗来纳州).
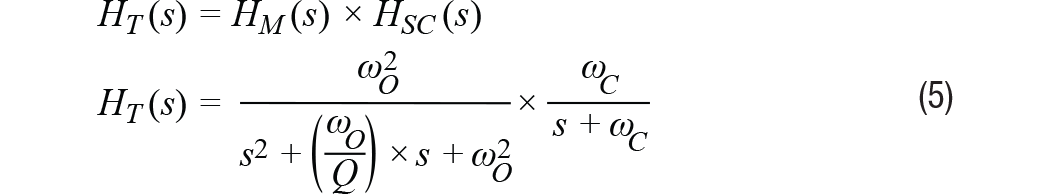
图3提供了该模型用于预测ADXL356(x轴)频率响应的直接应用。该模型假设标称谐振频率为5500 Hz,Q为17,并使用截止频率为1500 Hz的单极点低通滤波器。 注意,公式5和图4仅描述了传感器的响应。此模型不包括考虑加速度计耦合到它所监视的平台的方式。
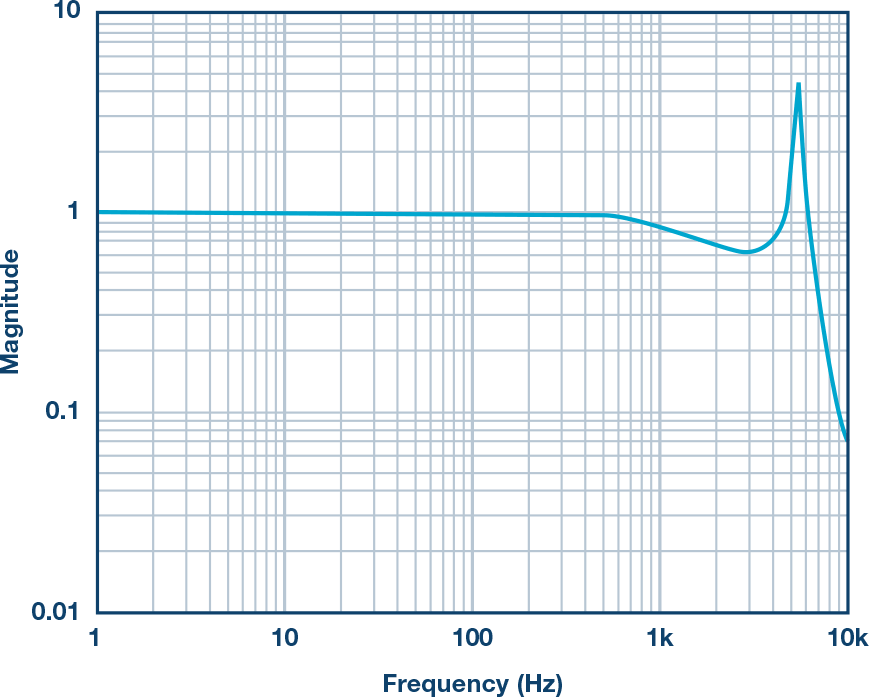
图3.ADXL356频率响应
带宽与平坦度
在利用单极点低通滤波器(如公式4中的滤波器)建立频率响应的信号链中,其带宽规格通常标识其输出信号提供输入信号功率50%的频率。在更复杂的响应中,例如公式5和图3中的三阶模型,带宽规格通常会附带相应的平坦度属性规格。平坦度属性描述比例因子在频率范围(带宽)内的变化。使用图3和公式5中的ADXL356仿真,1000 Hz时的平坦度约为17%,2000 Hz时的平坦度约为~40%。
虽然许多应用由于其平坦度(精度)要求而需要限制它们可以使用的带宽,但在某些情况下,这可能并不那么令人担忧。例如,某些应用程序可能更侧重于跟踪随时间推移的相对变化,而不是绝对准确性。另一个例子可能来自那些将利用数字后处理技术来消除他们最感兴趣的频率范围内的纹波的人。在这些情况下,响应的可重复性和稳定性通常比给定频率范围内的响应平坦度更重要。
测量范围
MEMS加速度计的测量范围指标表示传感器在其输出信号中可以跟踪的最大线性加速度。在超出测量范围额定值的某个线性加速度水平下,传感器的输出信号将饱和。发生这种情况时,它会引入明显的失真,并且很难(如果不是不可能的话)从测量中提取有用的信息。因此,确保MEMS加速度计支持峰值加速度水平非常重要(参见.MAX在图 2 中)。
请注意,测量范围将取决于频率,因为传感器的机械响应会给响应带来一些增益,增益响应的峰值发生在谐振频率处。在ADXL356的仿真响应中(见图3),增益峰值约为4×,从而将测量范围从±40 g减小到±10 g。公式6提供了一种分析方法来预测相同的数字,使用公式5作为起点:
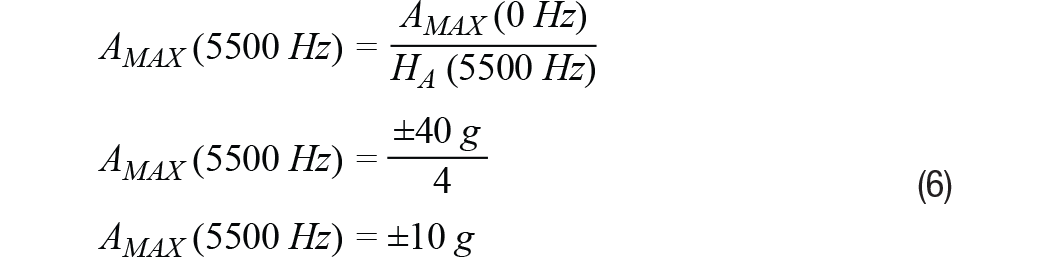
比例因子的大幅变化和测量范围的缩小是大多数CBM系统希望将其振动暴露的最大频率限制在远低于传感器谐振频率的水平的两个原因。
分辨率
“仪器的分辨率可以定义为环境中导致仪器指示发生可检测变化的最小变化。”1在振动检测节点中,加速度测量中的噪声将直接影响其检测振动变化的能力(也称为“分辨率”)。因此,对于那些正在考虑使用MEMS加速度计来检测其机器平台上振动的微小变化的人来说,噪声行为是一个重要的考虑因素。公式7提供了一个简单的关系,用于量化MEMS加速度计噪声对其分辨微小振动变化的能力的影响。在此模型中,传感器的输出信号(yM) 等于其噪声之和 (aN)及其正在经历的振动(aV).由于噪声之间没有相关性(aN)和振动(aV)、传感器输出信号的大小 (|yM|)将等于噪声幅度 (|a 的和方根 (RSS) 组合N|)和振动幅度(|AV|).

那么,需要多大的振动水平才能克服测量中的噪声负担并在传感器的输出信号中产生可观察的响应?根据噪声水平量化振动水平有助于以分析方式探索这个问题。等式8通过比率(KVN),然后推导出一个关系,以预测传感器输出的变化水平,根据该比率:
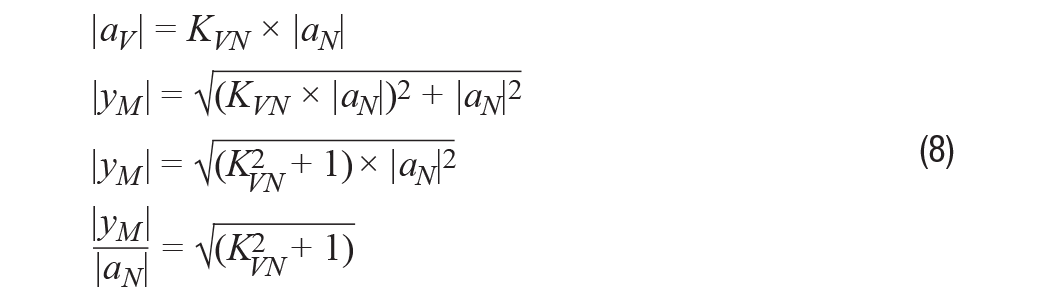
表1提供了这种关系的一些数值示例,以帮助说明传感器输出测量值相对于比率(KVN)的振动和噪声幅度。为简单起见,本讨论的其余部分将假设传感器测量中的总噪声将确定其分辨率。从表1中,这与KVN等于 1,即振动幅度等于噪声幅度。当这种情况发生时,当零振动时,传感器输出的幅度将比其输出幅度增加42%。请注意,每个应用程序可能需要考虑其系统中可观察到的增长水平,以便在这种情况下建立解决的相关定义。
| KVN |
的ML/LANl |
增加 % |
| 0 | 1 | 0 |
| 0.25 | 1.03 | 3 |
| 0.5 | 1.12 | 12 |
| 1 | 1.41 | 41 |
| 2 | 2.23 | 123 |
预测传感器噪声
图4显示了将使用MEMS加速度计的振动检测节点的简化信号链。在大多数情况下,低通滤波器为抗混叠提供了一些支持,而数字处理将在频率响应中提供更明确的边界。通常,这些数字滤波器将寻求保留代表真实振动的信号内容,同时最大限度地减少带外噪声的影响。因此,在估算噪声带宽时,数字处理通常是系统中需要考虑的最有影响力的部分。这种类型的处理可以采用时域技术的形式,例如带通滤波器,也可以采用光谱技术,例如快速傅立叶变换(FFT)。
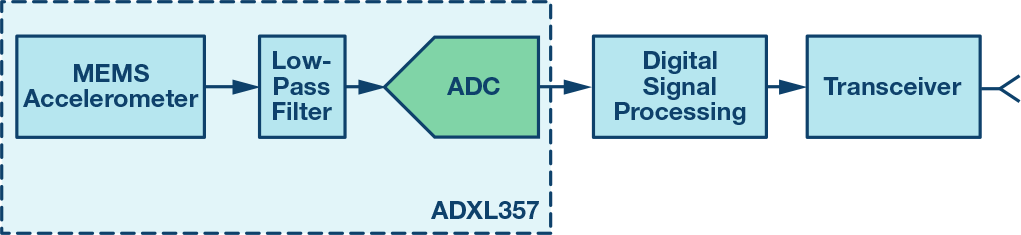
图4.振动检测节点的信号链。
公式9提供了估算MEMS加速度计测量中总噪声的简单关系(A噪声),使用其噪声密度 (φND) 和噪声带宽 (fKB2) 与信号链相关联。

利用公式9中的关系,我们可以估计,在ADXL357上使用噪声带宽为100 Hz的滤波器(噪声密度= 80 μ g/√Hz)时,总噪声将为0.8 mg (rms)。
速度方面的振动
一些CBM应用需要根据线速度评估核心加速度计的行为(范围、带宽、噪声)。进行这种转换的一种方法是从图1中的简单模型和公式1中生成模型的相同假设开始的:线性运动、单频和零平均位移。等式10通过瞬时速度(vV) 中的对象。该速度的大小以均方根 (rms) 表示,等于峰值速度除以 2 的平方根。

等式11采用这种关系的导数来生成图1中物体瞬时加速度的关系:
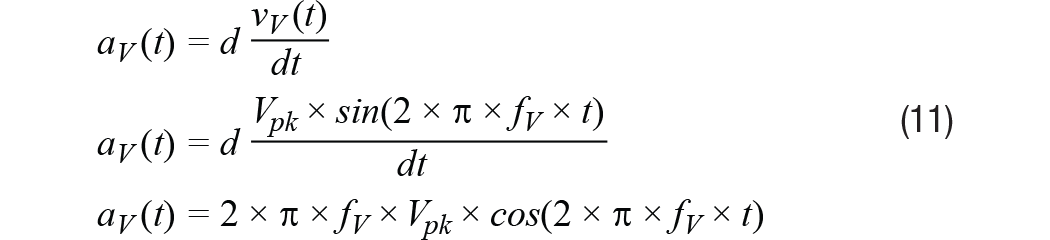
从公式11中加速度模型的峰值开始,公式12推导出一个新的公式,该公式与加速度大小(A有效值) 到速度大小 (V有效值)和振动频率(fV).

个案研究
让我们结合ADXL357的案例研究,该案例研究以线速度表示其在1 Hz至1000 Hz振动频率范围内的范围(峰值)和分辨率。图5提供了有助于本案例研究的几个属性的图形定义,首先是ADXL357在1 Hz至1000 Hz频率范围内的噪声密度图。为了简单起见,本特定案例研究中的所有计算都将假设噪声密度是恒定的(φND= 80 μg/√Hz) 在整个频率范围内。图5中的红色频谱图表示带通滤波器的频谱响应,绿色垂直线表示单个频率的频谱响应(fV)振动,这对于开发基于速度的分辨率和范围估计很有用。
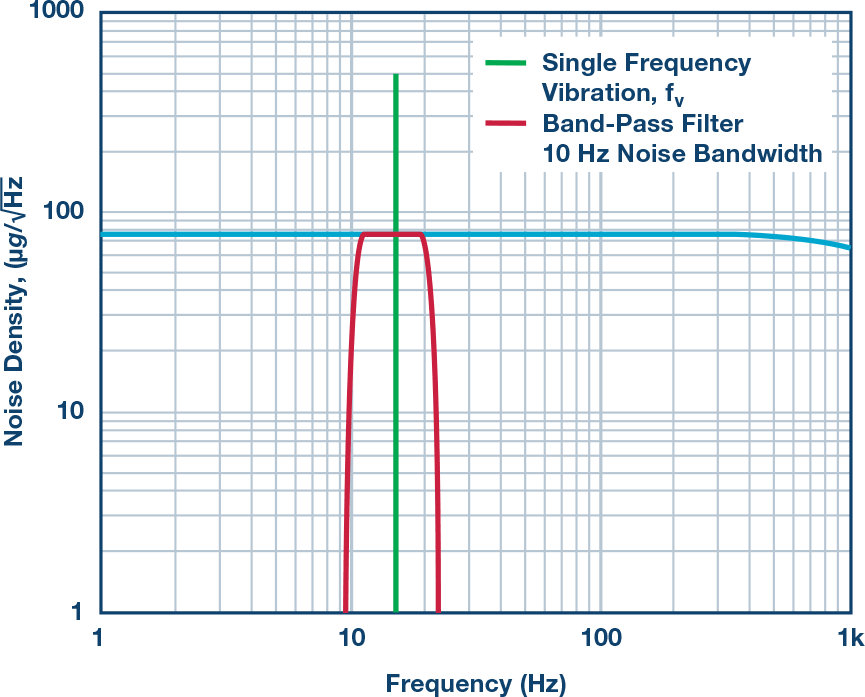
图5.案例研究噪声密度和滤波。
该过程的第一步使用公式9来估计噪声(A噪声),来自四种不同的噪声带宽 (fKB<>):1 Hz、10 Hz、100 Hz 和 1000 Hz。 表 2 以两种不同的线性加速度测量单位表示了这些结果:g 和 mm/s2.g的使用在大多数MEMS加速度计规格表中相当普遍,而振动指标在这些术语中并不常见。幸运的是,g和mm/s之间的关系2是相当众所周知的,可在公式13中找到。

| fKB<>(赫兹) | 一个噪声 | ||
| (米克) | (毫米/秒2) | ||
| 1 | 0.08 | 0.78 | |
| 10 | 0.25 | 2.48 | |
| 100 | 0.80 | 7.84 | |
| 1000 | 2.5 | 24.8 | |
本案例研究的下一步将重新排列公式12中的关系,以推导出一个简单的公式(参见公式14),用于将总噪声估计值(来自表2)转换为线速度(VRES/ 5峰).除了提供这种关系的一般形式外,公式14还提供了一个具体示例,使用10 Hz的噪声带宽(加速度噪声为2.48 mm/s)。2,来自表 2)。图6中的四条虚线表示所有四个噪声带宽相对于振动频率(fV).
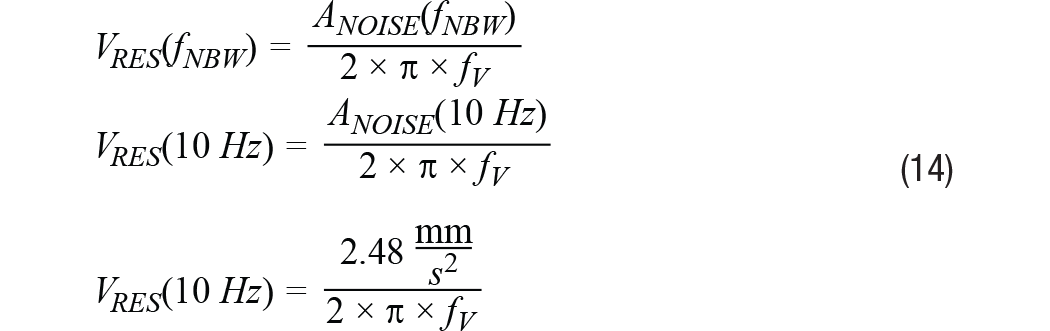
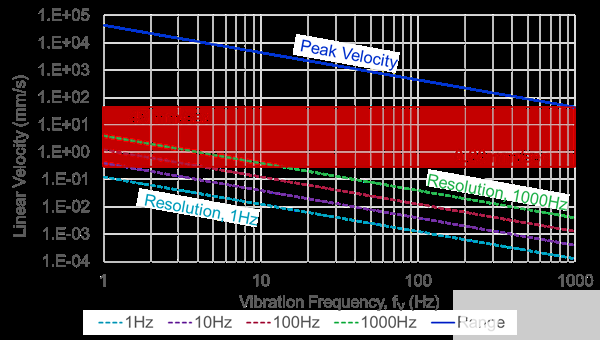
图6.峰值和分辨率与振动频率的关系。
除了显示每个带宽的分辨率外,图6还提供了一条蓝色实线,表示相对于频率的峰值振动水平(线速度)。这来自公式15中的关系,其开头与公式14的一般形式相同,但不是使用分子中的噪声,而是使用ADXL357可以支持的最大加速度。请注意,假设单频振动模型,分子中的 √2 因子会缩放此最大加速度以反映均方根水平。
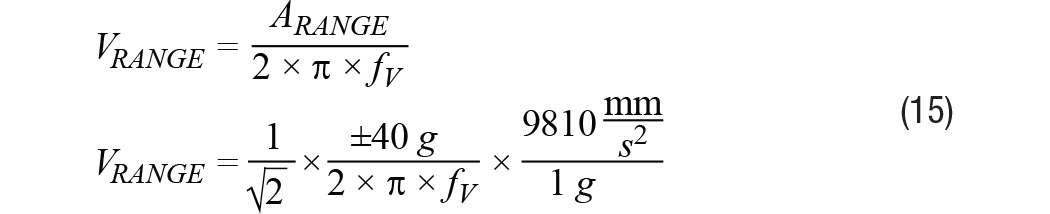
最后,红框表示如何将此信息应用于系统级要求。此红框中的最小 (0.28 mm/s) 和最大 (45 mm/s) 速度级别来自机器振动通用行业标准中的一些分类级别:ISO-10816-1。叠加ADXL357的范围和分辨率图的要求,提供了一种进行简单观察的快速方法,例如:
测量范围最坏的情况是在最高频率下,ADXL357的±40 g范围似乎能够测量与ISO-10816-1相关的大部分振动曲线。
当使用噪声带宽为10 Hz滤波器的滤波器处理ADXL357的输出信号时,ADXL357似乎能够在1.5 Hz至1000 Hz的频率范围内分辨ISO-10816-1 (0.28 mm/s)的最低振动水平。
当使用噪声带宽为1 Hz滤波器的滤波器处理ADXL357的输出信号时,ADXL357似乎能够在整个1 Hz至1000 Hz频率范围内解析ISO-10816-1的最低振动电平。
结论
MEMS加速度计作为振动传感器正在成熟,它们在现代工厂CBM系统中技术融合的完美风暴中发挥着关键作用。传感、连接、存储、分析和安全方面的新解决方案汇集在一起,为工厂经理提供完全集成的振动观察和过程反馈控制系统。虽然很容易迷失在所有这些惊人的技术进步的兴奋中,但仍然需要有人了解如何将这些传感器测量与现实世界的条件以及它们所代表的含义联系起来。CBM开发人员及其客户将能够从这些简单的技术和见解中获取价值,这些技术和见解提供了一种使用熟悉的度量单位将MEMS性能规格转化为其对关键系统级标准的影响的方法。
审核编辑:郭婷
-
MEMS加速度计基本振动特性2023-11-28 561
-
MEMS加速度计的振动校正介绍2023-11-23 410
-
MEMS振动检测:速度到加速度2023-01-04 1913
-
MEMS加速度计中的振动校正是如何发生的?2021-02-26 2115
-
MEMS加速度传感器在电机健康状态监测上的应用2020-04-23 4451
-
MEMS加速度计如何选择2019-07-25 2490
-
数据说话,今非昔比的MEMS加速度计你真的了解吗?2018-11-01 2859
-
MEMS加速度计性能成熟2018-10-29 2805
-
MEMS加速度计性能已臻成熟2018-10-23 2213
-
从一份案例研究MEMS加速度计的振动校正2018-10-22 1767
-
检测监控系统中的MEMS加速度振动2018-06-12 2683
-
MEMS振动监控:从加速度到速度2017-08-16 5979
-
基于MEMS加速度计的振动监控解决方案2017-08-08 8111
全部0条评论

快来发表一下你的评论吧 !

