高分辨率、实时的手持物体360°三维模型重建结构光技术

摘要

真实物体完整形状的数字化在智能制造、工业检测和反向建模等领域具有重要的应用价值。为了构建刚性对象的完整几何模型，对象必须相对于测量系统（或扫描仪必须相对于对象移动），以获取和集成对象的视图，这不仅使系统配置复杂，而且使整个过程耗时。在这封信中，我们提出了一种高分辨率的实时360°三维(3D)模型重建方法，该方法允许人们手动旋转一个物体，并在扫描过程中看到一个不断更新的三维模型。多视图条纹投影轮廓测量系统从不同的角度获取一个手持物体的高精度深度信息，同时将多个视图实时对齐并合并在一起。我们的系统采用了立体相位展开和自适应深度约束，可以在不增加捕获图案的数量的情况下，稳健地展开密集条纹图像的相位。然后，我们开发了一种有效的从粗到细的配准策略来快速匹配三维表面段。实验结果表明，该方法可以在任意旋转条件下重建复杂物体的高精度完整三维模型，而无需任何仪器辅助和昂贵的预/后处理。

引言

光学非接触式三维(3D)形状测量技术已广泛应用于工业检测、智能制造、逆向工程等许多方面的[1]。边缘投影轮廓测量(FPP)[2,3]由于其高测量精度、简单的硬件配置和实现的灵活性，是最流行的三维成像技术之一。到目前为止，大多数关于FPP的研究都集中在单一角度的三维测量上。然而，在工业检查和反向建模等应用中，获取所有对象的三维模型是至关重要的。然而，传统的FPP系统由于其视场有限，无法在单次测量中获得目标的完整三维模型，因此需要对从多个视图测量的数据进行配准。 为了从不同的视图获得和对齐物体的三维形状，通常需要仪器辅助来执行三维配准[7–9]。常见的辅助仪器包括旋转台、机械臂和平面反射镜。通过旋转台，通过旋转台轴的旋转与成像系统[7]之间的关系，可以将多帧点云转换为相同的坐标系。但物体只能围绕旋转台轴旋转，难以获取顶部、底部的三维数据。机械臂可以通过预置一个移动路径[8]来从更多的角度获取信息。然而，机械臂的成本很高，辅助系统需要复杂的硬件连接，因此实现此类系统是困难的。带有两个镜子的测量系统可以在一个测量中重建一个全景三维表面，因为它们同时从三个角度捕捉目标[9]。然而，由于透视信息有限，这类系统仍然无法获得全尺度的三维测量。 由于昂贵的硬件设施、复杂的结构或有限的视角信息，上述仪器辅助配准方法并不是获得360°3D模型的理想手段。理想的方法是在连续执行实时三维配准的同时，任意旋转对象的三维数据。到目前为止，很少有人报道过这种方法，因为（1）由于硬件技术和实时算法的限制，构建基于FPP的动态对象实时，高精度3D测量系统是困难的[4,10]; 无辅助仪器的不间断实时高精度三维配准是一个非常具有挑战性的[11]。2002年，鲁辛克维茨等人[12]提出了一种基于结构光测距仪和迭代最近点(ICP)算法的实时变体的实时三维模型采集方法。与以前的方法相比，它允许用户手动旋转一个对象，并看到一个不断更新的模型，从而提供关于孔的存在和已被覆盖的表面的即时反馈。然而，通过条纹边界编码策略获得的点云相当稀疏，使得三维数据积累过程的效率降低。此外，他们的配准方法的精度较低，因为它们跳过了传统的仪器辅助粗配准，直接进行基于变异icp的精细配准，而没有得到良好的姿态估计。因此，要重建一个高精度的三维模型，就需要进行耗时的后处理。 在这封信中，我们首次在没有任何仪器辅助的情况下，实现了对物体的360°三维模型的实时采集，总体精度高达100μm级。用我们的方法，我们可以手工任意旋转物体。由于从单一角度获取对象的三维数据，可以自动与前一帧的三维数据进行实时配准，并合并在一起，创建一个高精度的三维模型。

方法

为了实现实时的三维配准，必须实时获取每个视角的三维数据。FPP的两种主流条纹分析方法分别是单镜头性质的傅里叶变换轮廓测量[13,14]和相移轮廓测量(PSP)[15]，以较高的测量分辨率和精度而闻名。考虑到精度，我们选择了后一种技术。由于运动会导致帧间的相位误差，并打破PSP的基本假设，因此应该采用尽可能少的条纹图案的PSP。因此，采用了三步移相法。通过三步移相模式，可以很容易地获得物体的包裹相位。为了展开相位，传统的方法是使用时间相位展开技术[16]。然而，需要大量的辅助条纹图案，这增加了对运动的灵敏度。在这封信中，我们使用立体相位展开(SPU)[17,18]方法来消除相位歧义，而不使用任何额外的辅助模式。

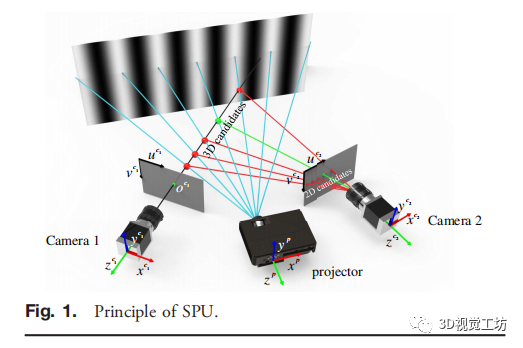
图1：立体相位展开（SPU）原理图 SPU的工作原理如图1所示。对于相机1中的任意点oc1，它有N个可能的绝对相位，通过相机1和投影仪可以重建N个3D候选点。这些3D候选点可以投影到Camera2上得到N个2D候选点，其中必须有一个与oc1最相似的正确匹配点。然后进行相位相似性检查，找到匹配点，也可以解开oc1的包裹相位。然而，SPU不能稳健地消除相位模糊，因为在噪声和系统误差的影响下，错误的候选点的相位可能比正确的点更接近oc1，而边缘频率越高，那么这种情况发生的可能性就越大。自适应深度约束(ADC)[19]策略可以通过实时测量结果提供一个像素级的深度范围，并在很大程度上排除了错误的3D候选对象。因此，我们使用ADC来提高SPU的稳定性。 接下来，我们将讨论实时、高精度的三维配准。有两种：（1）直接进行精细配准，（2）在粗配准后进行精细配准。第一类方法直接使用ICP算法[20]及其改进的变体。然而，由于缺乏合适的初始姿态估计，ICP效果不佳。此外，ICP通常需要花费更高的配准精度，并且不适用于实时场景。然而，在没有仪器辅助的情况下，执行快速粗配准并不简单。在这篇论文中，我们改进了同步定位和映射(SLAM)算法[21]，用于机器人的定位和地图构建，以执行粗配准。将两个相邻的3D帧定义为帧1和帧2，它们具有对应的2D纹理映射I1和I2，和相机坐标系下的3D数据：

图2 检测到的2D特征点（a）通过SIFT和欧氏距离匹配的点（b）通过我们的方法优化后的点

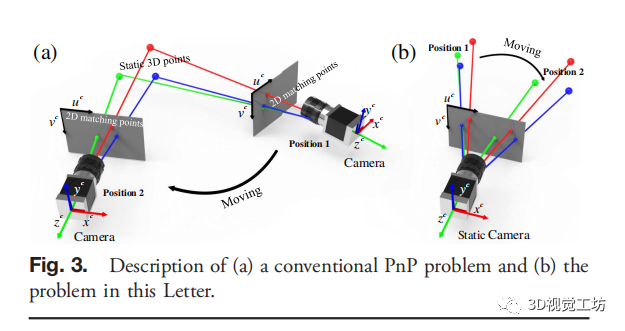
图3 描述：（a）传统PnP方法（b）我们问题的描述 在快速进行二维匹配点识别后，利用求解多视角(PnP)问题的方法，可以快速得到相邻三维帧之间的变换矩阵，这是一种常用的从三维参考点间的n个对应关系中估计摄像机姿态的技术。获取相机姿态的常规PnP问题如图3(a)所示，即当物体保持静止时相机移动，我们知道物体在世界坐标系中的三维数据和相机移动到位置2时的像素坐标。在本文中，PnP问题可以看作是如何求解成像系统静止时运动物体的变换矩阵，并知道物体移动前的三维数据和物体移动后的像素坐标，如图3(b)所示。我们采用EPnP方法[23]，这是一个PnP问题的非迭代解，由于其精度和效率的平衡来解决PnP问题，在视觉SLAM系统中被广泛应用。

图4：结果：（a）粗配准（b）精配准  

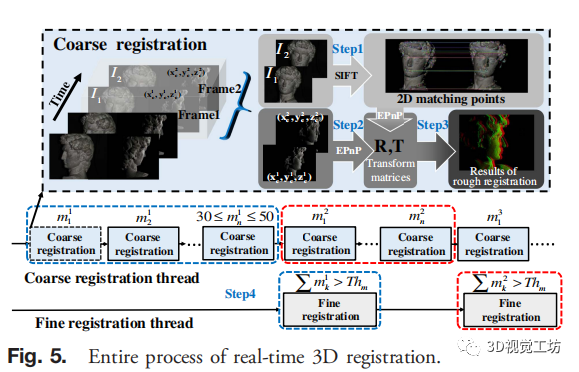
图5：实时3D配准的流程 实时三维配准的整个过程如图5所示。步骤1：利用SIFT算法找到二维匹配点，并利用相应的三维数据对其进行优化；步骤2：采用EPnP方法得到变换矩阵；步骤3：粗配准线程粗配准点云，保留运动在30到50之间的结果；步骤4：如果累积运动达到阈值，在精细配准线程中降采样后执行ICP算法，实现点云的精确配准；步骤5：返回到步骤1，并重复上述过程。

实验

为了验证我们的算法的有效性，我们构建了一个四相机3D成像系统，包括一个轻型4500Pro(100Hz速度)，三个用于SPU的acA640-750um相机（640×480分辨率）和一个用于彩色纹理的acA640-750uc相机。使用了48段PSP条纹。我们使用一台HPZ230计算机(IntelXeonE3-1226v3CPU，NVIDIAQuadroK2200GPU)来开发我们基于OpenCV和PCL的算法。我们的软件系统的接口是用Qt软件开发的。该系统的成像速度为45Hz，单次扫描精度为45μm。

图6：David 模型的场景以及配准结果（整个过程请看可视化1）

图7：David模型配准后的结果（a）点云结果（b）（a）的三角化结果 在第一个实验中，我们任意旋转了David模型，实现了其360°建模。不同时间段的配准结果和场景如图6所示。单次粗配准和细配准的时间分别为0.4s和2s。整个模型的重建时间是70秒。图7显示了配准后的结果，从中我们可以看到David模型的所有3D形状都很好地对齐。实验结果表明，该方法可以实时获得高质量的360°手持物体三维模型。

图8：David模型与陶瓷球配准结果（a）,（b）：两个视角的测量图像（c），（d）相应的配准结果（e），（f）：球配准的误差分布 在第二次实验中，测量了两个半径分别为25.3989和25.4038mm的陶瓷球，中心间距离为100.0532mm。由于球体没有二维特征，所以它们可以借助David模型进行注册。测量结果如图8所示。对两个球体的测量结果进行了球面拟合。它们的误差分布如图所示。8(e)和8(f)。整个重建球的半径分别为25.3580和25.3543mm，偏差分别为40.9μm和49.5μm。测量到的中心-中心距离为99.9345mm，误差为118.7μm。本实验表明，该方法重建的整个三维模型的总体精度可达到100μm水平。

结论

总之，据我们所知，我们首次提出了一种基于FPP的高分辨率实时360°三维模型重建技术。与以往传统的复杂、耗时的三维模型采集系统相比，我们的设计允许用户手动旋转物体，并在被扫描物体时看到不断更新的模型。最后，可以获得一个精度高达100μm水平的完整的三维模型。这封信使低成本、高速、高精度、任意自动的3D配准、快速反馈和易于使用的全方位三维实时建模成为可能。我们相信，这封信将为360°的工业检测和快速逆向成型打开一扇新的大门，并具有广阔的应用前景。

审核编辑 ：李倩