基于MSP430F1611单片机的音频信号分析

 

 

　　本系统将采用集成有μC/OS-Ⅱ操作系统的单片机，利用快速傅里叶变换并加窗函数的方法来实现对音频信号各项参数的分析。

　　1 系统总体方案

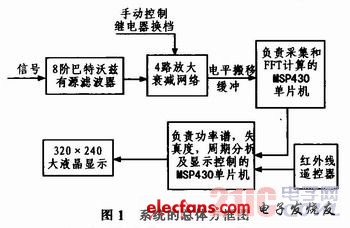
　　信号首先通过8阶有源巴特沃兹滤波器进行抗混叠处理，然后通过放大衰减，电平搬移缓冲网络后，送单片机处理。

　　系统的2片MSP430F1611单片机，一片负责对模拟信号进行采样，并对采集得到的信号进行4096点的FFT计算，另一片负责控制显示设备以及完成对信号功率谱，周期性，失真度的分析。

　　系统的总体方框图如图1所示。

　　

 

　　2 系统各硬件设计

　　2.1 抗混叠滤波器的设计

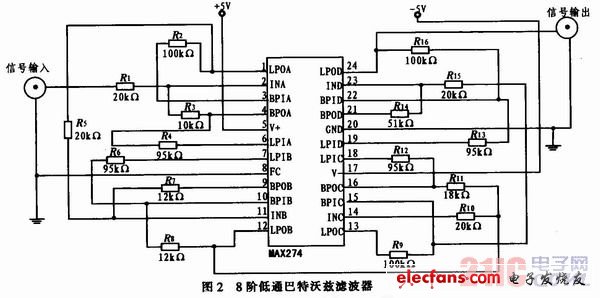
　　根据Nyquist定理，AD模数转换器以fs的频率采样输入信号时，频率f>fs/2的信号将被关于fs/2的频率镜像到2fs-f处，带外杂散信号所引起的混叠现象如果没有经过适当的滤波处理，这些频率成分将会影响到带内数据采集的性能指标。本系统选择了约40 kHz的换档采样频率，而输入信号最高为10 kHz，过采样率较低，故对滤波器提出了比较高的要求。考虑到巴特沃兹滤波器平坦的带内幅频特性，使用了连续时间有源滤波器MAX274设计了8阶的巴特沃兹滤波器(如图2所示)，使20 kHz外的信号得到有效地衰减，经过试验，效果比较好。

　　

 

　　2.2 前端放大器的设计

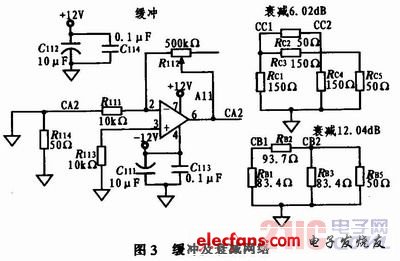
　　由于输入音频信号的幅度可能会较大，我们假设外界给予的信号能达到10 V峰峰值，而MSP430F1611单片机片内AD采集信号范围为0～2.51 V，故需将信号进行压缩。经综合考虑，本系统分为4档，并保证每档都有重叠的部分。100 mV以下通过低失调运放op07放大27.6 dB(24倍)，90 mV～2.5V范围内直通，而在2～5 V范围内通过电阻分压衰减6.02 dB(2倍)。同样在4～10 V范围内衰减12.04 dB(4倍)，然后通过输入设备进行手动选档，控制每路继电器的通断，选择到最适合的档位，再将此信号经过电平搬移电路后缓冲输入单片机采样进行FFT计算。本模块在级联时注重了对前后级的隔离，加入了缓冲级，使测量信号幅度的误差减小，如图3所示。

　　

 

　　2.3 音频信号周期性的判断及周期测量

　　本系统通过设定功率门限值，能有效地判断所送入的信号是否具有周期性，并计算出周期信号的周期值。对于一般的周期信号f(t)，将f(t)展开成傅里叶级数得：

　　

 

　　将式(1)两边取傅里叶变换得：

　　

 

　　可看出一般的周期信号是由一系列的冲激函数组成的离散频谱，且冲激发生在信号的谐波频率处(0，±w1，±2w2...)，而非周期信号的频谱是连续的，所以信号频谱分布较分散，在频谱上不可能有大的阶跃，这样可通过设定一功率门限值，如果有大于此门限值的频谱存在就是周期信号，反之则不是，当判断信号为周期信号时，将信号送入比较器，产生的脉冲信号送入单片机计数从而判断其周期。经过多次试验，选择一个较好的门限值，这样就能判断很大部分的信号(如三角波、锯齿波、正弦波)是否具有周期性，从而准确计算出信号的周期。

　　2.4 音频信号失真度的测量

　　对于正弦信号来说，基波频谱的功率值总是最大的，可通过此方法来判断基波的频谱，从而得到基波的功率。正弦信号的失真度定义为信号中全部谐波分量的能量与基波能量之比的平方根值，设正弦信号的基波功率为P1，信号的总功率为P，则正弦信号的失真度为

　　

 

　　通过所分析出来的各频谱功率即可计算出正弦信号的失真度。

　　3 系统软件设计

　　3.1 嵌入式系统设计

　　本设计在MSP430F1611单片机中嵌入了μC/OS-Ⅱ操作系统，可以很方便地实现多任务的调度与协调，极大地节约了软件开发时间和减少了出错几率。系统的软件流程图如下：图4为FFT的软件流程图，图5为负责信号采集并进行FFT计算的从机MSP430F1611的流程图，图6为负责外设信号分析的主机MSP430F1611的流程图。

　　

 

　　3.2 FFT算法的具体设计

　　3.2.1 FFT点数与采样频率的分析

　　本系统应用基2的傅里叶变换进行计算，考虑到使用的16位MSP430F1611单片机的RAM存储空间为10 k，由于经过FFT计算后谱线的幅值关于中心对称，为了节省硬件资源，将FFT计算后的2048个点舍去，故可节省一半的资源，由于2 048x16 bitx2=8.192 k，故最大取N=4 096个点作FFT。本系统将频率分辨力设定为20 Hz，如果取采样频率fs=40kHz，那么此FFT的频率分辨力△f=fs/N=10 Hz。但在实际情况下，由于FFT只能分析有限个点，必须对连续时间的信号进行截断，相当于在时域信号加了一个窗，使信号频谱向两边扩散产生频谱泄漏效应;再加上FFT的频率分辨力有限，使信号频谱不能完全与FFT的谱线重合，从而产生栅栏效应，这两种效应使分析出来的谱线扩散分布;对两个相距只有20 Hz的信号，所以可采取提高FFT的频率分辨力△f即减小采样频率或提高FFT点数，或通过加窗的方法来更精确地分析频谱。本系统将所采集信号的频率分成两段，当信号频率较高时，可利用fs=40 kHz的采样频率采样，当所采集信号的频率较低时，通过输入装置改变采样频率至fs=20kHz，这样FFT的采样频率甚至可提高到△f=fs/N=5 Hz，通过此方法可提高整体系统的频率分辨力，而分析FFT的点数受到硬件资源的限制，最后也可通过加窗的方法来提高分析精度。

　　3.2.2 窗函数的选择

　　不同的窗函数对信号会产生不同的作用，旁瓣幅度比较小的窗函数有利于减小频谱泄漏，对信号频谱幅值的测量较为准确，但这种窗函数的主瓣宽度较大，会使分析出来的谱线向两边扩散得比较多，导致测量单频，多频信号频率的准确度下降，如blackman窗，Flattop窗等。而旁瓣幅度衰减较弱的窗函数主瓣宽度较窄，这样有利于对频率准确度的测量，如矩形窗，也有兼顾两者的如banning窗，bumming窗等。所以频率与幅度的测量准确性是矛盾的。本系统利用matlab仿真初步估计应选用的窗函数，所分析的信号为单频率函数

　　

 

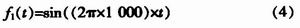
　　将此信号加上各窗函数后的matlab仿真结果如下：图7为加blackman窗后的频率谱线，图8为加hanning窗后的频率谱线。

　　

 

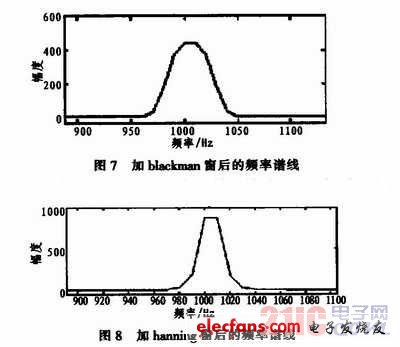
　　根据上图可以看出1 000 Hz和1 005 Hz的频谱被分成了几根幅值比较高的谱线，这是由于泄漏效应与栅栏效应所造成的，当加banning窗时，信号频率刚好是FFT频率分辨率fs/N=10 Hz的整数倍时，信号谱线分成了7根幅值比较高的谱线。当加blackman窗时，谱线分成了将近20根幅值较高的谱线。但在实际情况下，当加hanning窗时，中心谱线处分成了3或4根幅值比较大的谱线，比仿真结果要好些，但加blaekman窗谱线分布得比仿真结果更广，但计算出来的幅度值会比banning窗的精度稍微高些，为了提高音频分析仪的频率分辨力，应尽量使相邻的谱线不相互重叠，这样才能计算各个频率信号的功率和提高频率分辨力，经过综合考虑，本系统选择加hanning窗。

　　4 测试方法与测试结果

　　4.1 测试环境及测试仪器

　　对该音频信号分析仪在30℃室温下进行测试，测试仪器如下：南京盛普40 M函数发生器2台，泰克60 M数字示波器1台，晶体管毫伏表DA-16，失真度测试仪ZC4128。

　　4.2 信号功率谱的测量

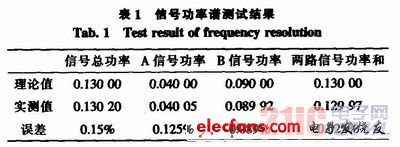
　　使用两台函数发生器产生两路信号进行叠加后测试，A，B两路输入电压为VppA=2.000 V(0.04 W)，频率为1 kHz，VppB=3.000V(0.09 W)，频率为1 kHz。表1为测试的结果，可知单信号功率谱测量误差在0.2%之内，而总功率测量误差也在0.2%左右。

　　

 

　　4.3 信号频率分辨率及周期性的测量

　　通过函数发生器输入一般的周期信号，输入50 Hz的正弦波，以及1 000 Hz的方波，三角波，锯齿的周期波和非周期噪声信号，表2为测试结果，可见对一般的信号的周期性判断很准确，频率测试误差在1%以内。

　　

 

　　4.4 信号失真度的测量

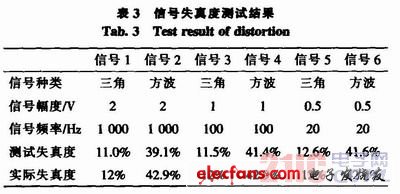
　　用函数发生器分别产生1 000 Hz、100 Hz、20 Hz的三角波以及1 000 Hz、100 Hz、20 Hz的方波，并将各信号分成两路，一路送失真度测试仪，一路送音频信号分析仪，通过对比所得结果来判断测试的精度。表3为测试结果，可见由于1 k左右的的谐波分量较高，抗混叠滤波器将高次谐波的能量滤除，故会使失真度偏差较大，当信号的频率降低时，失真度会测量得比较准确。

　　

 

　　5 结束语

　　本系统利用快速傅里叶变换(FFT)的算法，综合外围采样电路，利用两块MSP430F1611单片机对信号进行处理，并借助了matlab工具进行预估计和判断，有效地减小了软件设计的盲目性。并通过加缓冲电路减小了前后级电路的相互影响，使音频信号分析仪的精度得到了有效地提高。