关于边缘检测算子的实现原理

当前，边缘检测算法在实际应用中越加广泛，技术趋势也是快速发展，热火朝天。很多朋友或多或少了解，需要实现各类功能，尤其是一些复杂的需求，实现更好的滤波、满足更佳的提取效果，一时半会儿无从下手。

下面小编就带大家了解关于边缘检测算子的实现原理。由于边缘检测算子常用方法较多（Sobel算子，Kirsch算子，Laplacian算子，Canny算子等），在此以Canny算子为例，带大家了解简单的实现原理。

边缘检测有什么作用？

 

简单通俗讲，边缘检测主要应用于一些数据信息的处理，提取想要的目标，剔除一些不相关的干扰及无用信息，通过更少的数据信息量获取更多关注的信息。

Canny算子简介

 

Canny 边缘检测算法 是 John F. Canny 于 1986年开发出来的一个多级边缘检测算法，此算法被很多人认为是边缘检测的最优算法，相对其他边缘检测算法来说其识别图像边缘的准确度要高很多。

最优边缘检测的特征：

低错误率: 标识出尽可能多的实际边缘，同时尽可能的减少噪声产生的误报

高定位性: 标识出的边缘要与图像中的实际边缘尽可能接近

最小响应: 图像中的边缘只能标识一次

Canny算子边缘检测流程

 

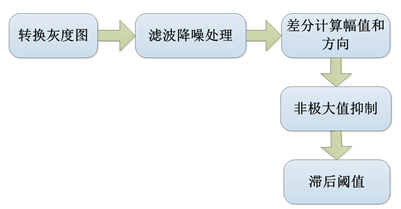
01 转换灰度

鉴于Canny算子只能对单通道灰度图像进行处理，因此在进行边缘检测之前需要将原图像进行灰度转换，以OpenCV为例，使用其封装的函数实现彩色到灰度的转换。

02 滤波降噪处理

完美的图像信息是无噪声的,图像质量很好,但是现实中由于采集设备、环境干扰等多方面的原因导致采集到的图像信息都是含有大量噪声信息的,这些噪声最常见的就是椒盐噪声和高斯噪声。

Canny算子是一种综合在抗噪声干扰和精确定位之间寻求最佳折中方案的边缘检测方法,一般使用高斯滤波来去除噪声,下面是常见的3X3的卷积核模板：

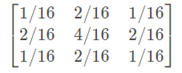
高斯滤波可以将图像中的噪声部分过滤出来，避免后面进行边缘检测时将错误的噪声信息也误识别为边缘了。

滤波核的维数不应选的过大，否则可能会将边缘信息给平滑掉，使得边缘检测算子无法正确识别边缘信息。

03 差分计算幅值和方向

使用一阶有限差分计算梯度可以得到图像在x和y方向上偏导数的两个矩阵，Canny算子中使用的是 Sobel 算子作为梯度算子，当然还可以自己构造其它的如：Roberts算子、Prewitt算子等一阶边缘检测算子来作为梯度算子。

下面以Sobel算子为例来计算梯度的幅值和方向：

【Y方向】 

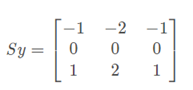
【X方向】

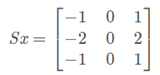
预设H（i , j）为计算的图像

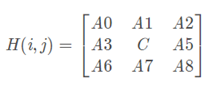
其中点C ( i , j ) 是要计算的梯度

【Y方向梯度】

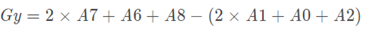
【X方向梯度】

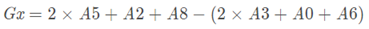
【此处C点的梯度幅值】

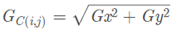
【此处C点的梯度方向】

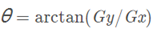
04 非极大值抑制

对非极大值的数据进行抑制，也可以理解成对非极大值数据排除其是边缘的可能性。8邻域内图像梯度幅值矩阵中的元素值越大，说明图像中该点的梯度值越大，再结合检测点的梯度方向，就可以定位出大概的边缘信息。

非极大值抑制两个特点：

当前位置的梯度值与梯度方向上两侧的梯度值比较

梯度方向是垂直于边缘方向

举例如下图所示

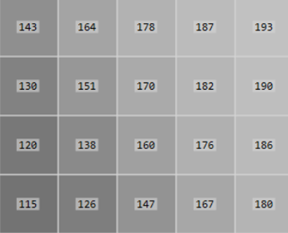
每个点的X方向和Y方向梯度方向矩阵

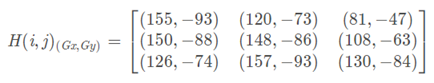
每个点的梯度方向的梯度角矩阵

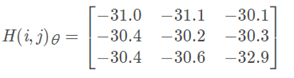
Canny算子将Gy/Gx的值求绝对值，OpenCV中的梯度角矩阵

每个点的梯度矩阵

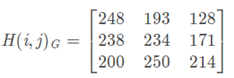
综上所示，计算出来的梯度值、梯度方向可以大致判断出此 8 邻域内的值的边缘信息如下图

梯度方向是同时包含多个梯度值的，因此需要将梯度方向两边的梯度值进行线性插值，插值系数β有如下要求：越靠近梯度方向的梯度值，其所占比例越大。

完成非极大值抑制后，会得到一个二值图像，非边缘的点灰度值均为0，可能为边缘的点灰度值为255。这样的一个检测结果还是包含了很多由噪声及其他原因造成的假边缘，还需要双阈值筛选处理。

05 滞后阈值

使用双阈值来对二值化图像进行筛选，通过选取合适的大阈值与小阈值可以得出最为接近图像真实边缘的边缘图像。

具体实现方法为：根据高阈值得到一个边缘图像，这样一个图像含有很少的假边缘，但是由于阈值较高，产生的图像边缘可能不闭合，解决该问题就采用了另外一个低阈值。

在高阈值图像中把边缘链接成轮廓，当到达轮廓的端点时，该算法会在断点的8邻域点中寻找满足低阈值的点，再根据此点收集新的边缘，直到整个图像边缘闭合。

编辑：黄飞