ADC中的集成容性PGA：重新定义性能

作者：Miguel Usach Merino and Gerard Mora Puchalt

获得专利的ADI电容可编程增益放大器（PGA）提供优于传统阻性PGA的性能，包括模拟输入信号的更高共模电压抑制。

本文介绍斩波电容放大器的工作原理，重点介绍当来自传感器的小信号需要在靠近电源轨的地方放大时，例如在温度测量（RTD或热电偶）和惠斯通电桥中，这种架构的优势。

Σ-Δ模数转换器（ADC）广泛用于具有小响应度和低带宽的传感器的应用，例如应变计或热敏电阻，因为这种架构提供了高动态范围。高动态范围背后的原因是与其他ADC架构相比，噪声性能较低。

Σ-Δ转换器的工作原理基于两个原理：过采样和噪声整形。当ADC对输入信号进行采样时，与采样频率无关的量化噪声会在整个频谱中传播到采样频率的一半。因此，如果输入信号的采样频率远高于奈奎斯特定理规定的最小频率，则目标频带中的量化噪声会降低。

图1显示了不同采样频率的量化噪声密度示例。

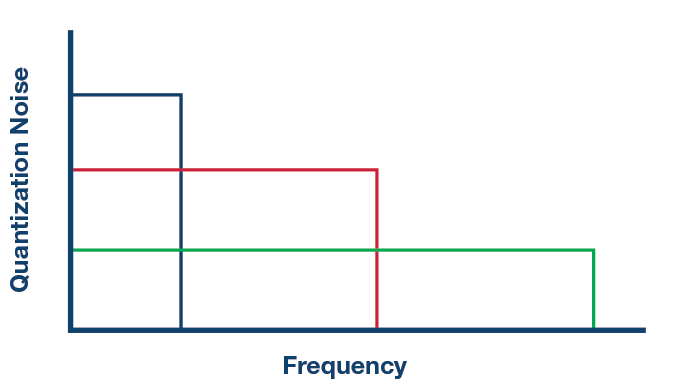
图1.不同采样频率随频率变化的量化噪声密度。

一般来说，对于给定的目标频段，过采样因子每为2，动态范围就会提高3 dB（假设白噪声频谱）。Σ-Δ转换器的第二个优点是噪声传递函数。如图2所示，它将噪声整形到更高的频率，从而进一步降低了目标频段的量化噪声。

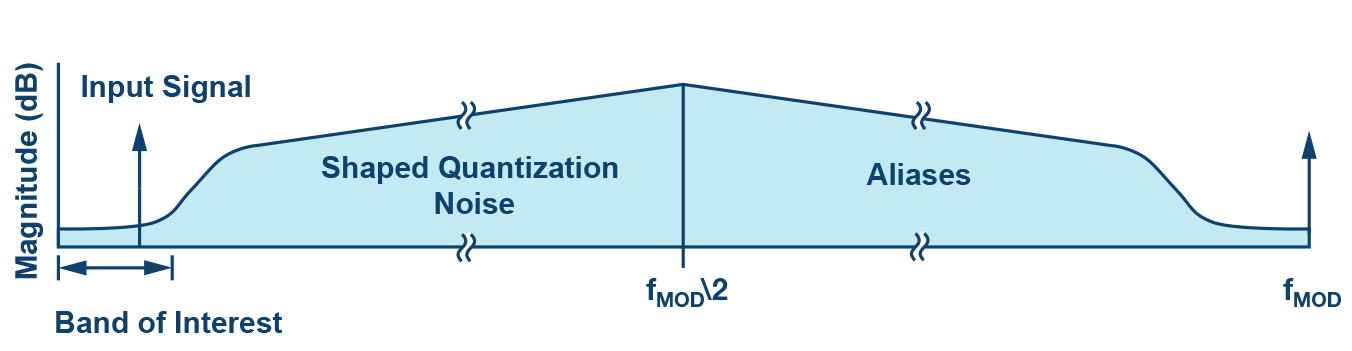
图2.Σ-Δ噪声整形。

此外，Σ-Δ可以集成数字滤波器，以消除目标频带之外的量化噪声，相当于出色的动态范围性能，如图3所示。

图3.LPF后的量化噪声。

输入缓冲器

过采样架构的缺点之一是，与在较低采样频率下工作的其他架构相比，驱动Σ-Δ调制器的输入缓冲器的要求可能会变得更加严格。采集时间变短，因此缓冲器需要更高的带宽。现代Σ-Δ转换器在片上集成了输入缓冲器，以最大限度地提高易用性。

此外，在传感系统中，为传感元件提供非常高的高精度输入阻抗对于测量精度至关重要。这使得对输入缓冲器的要求更加重要。

集成输入缓冲器会产生其他挑战。Σ-Δ调制器在低频时具有非常低的噪声，但输入缓冲器等任何其他组件都会增加热噪声，更重要的是，在低频时会增加闪烁噪声，如图4所示。

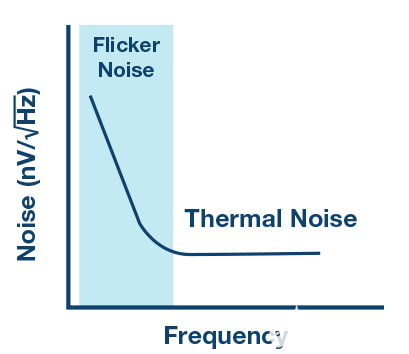
图4.闪烁噪音。

此外，缓冲器的偏移可能会导致整体系统误差。失调可以通过系统校准进行补偿，但如果失调漂移相对较高，这种方法可能变得不切实际，因为它要求每次工作温度变化时重新校准系统以补偿缓冲失调贡献。

例如，当失调漂移为500 nV/°C时，10°C的温度增量将相当于5 μV失调变化，在±2.5 VREF 24位ADC中，相当于16.8 LSB，约为4位。

解决这两个问题的典型方法是斩波缓冲器的输入和输出，如图5所示。

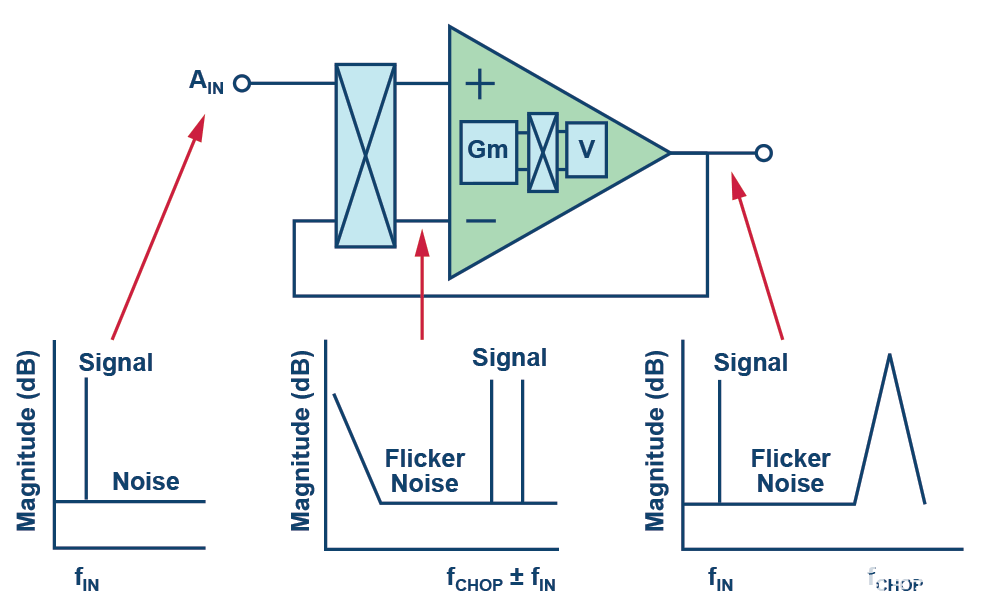
图5.斩波放大器。

通过斩波输入，输入频率被调制到更高的频率。缓冲失调和闪烁噪声保持在原来的低频，因为它们不受输入斩波的影响。

输出斩波器机制将输入频率解调回基带，同时将缓冲器增加的失调和闪烁噪声调制至更高的频率，这些频率将由ADC低通滤波器消除。

在某些情况下，输入缓冲器被基于电阻的仪表放大器（阻性PGA）取代，以在整个调制器输入范围内容纳小传感器信号，从而最大化动态范围。请注意，由于分立传感器需要更高的输入阻抗，因此基于电阻的仪表放大器优于差分电阻放大器。阻性PGA实现了类似的斩波方案，如图6所示。

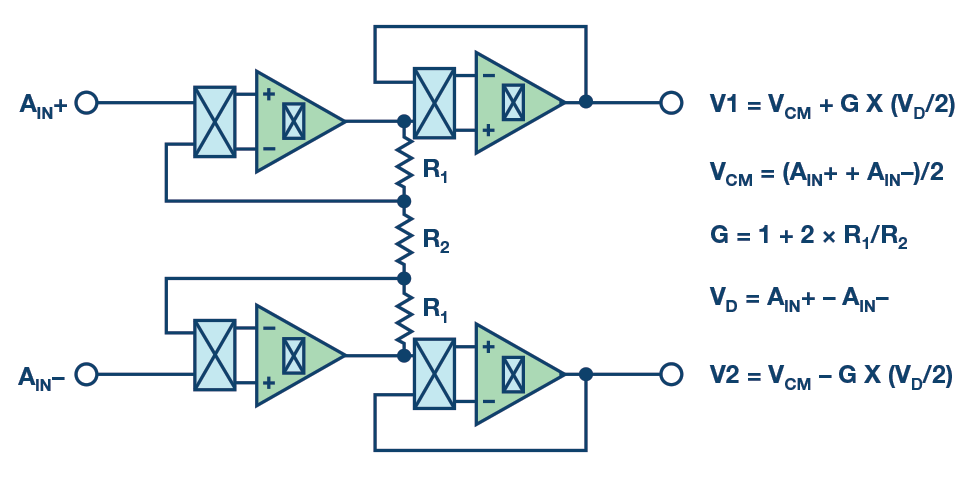
图6.电阻式PGA。

阻性PGA可能需要第二组级联连接的缓冲器，因为放大器可能无法提供足够的带宽来直接驱动调制器。同时，电流消耗应保持在较低水平，这决定了电阻的值，从而决定了放大器的带宽。

使用这种放大器拓扑的主要限制是共模电压的限制，特别是增益不是1，因为阻性PGA具有取决于输入信号的浮动共模，如图6所示。

此外，阻性网络失配及其漂移也是整体误差预算中的一个问题，因为它可能会影响大多数精密规格。

为了避免这些限制，最近的ADI Σ-Δ转换器采用了容性PGA。

电容式PGA放大原理与阻性PGA相似;增益取决于电容比，如图7所示。

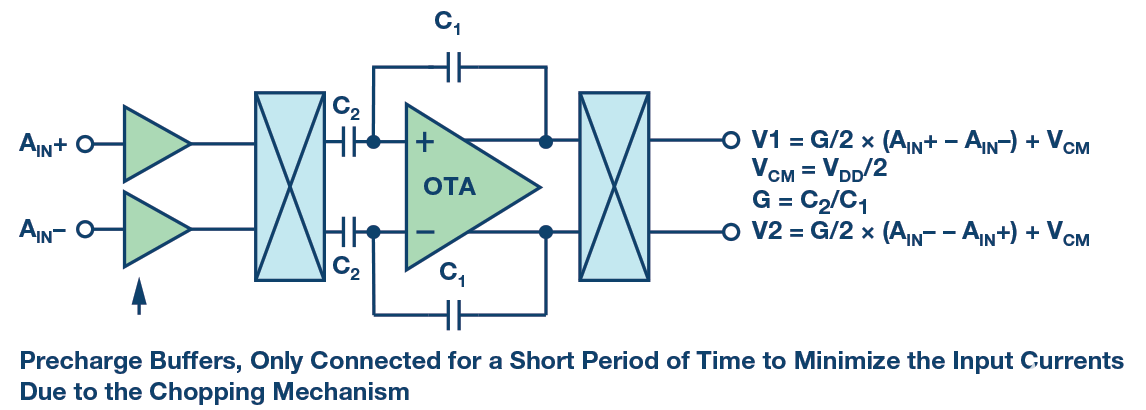
图7.电容式PGA（为清楚起见，已删除某些块）。

为了放大直流信号，电容PGA在PGA输入端引入斩波机制，将直流输入信号调制到斩波频率，然后由容性放大器放大。最后，信号通过输出斩波器解调回直流。此外，放大器失调和闪烁噪声被调制到斩波频率，并在稍后阶段进行低通滤波。

与阻性架构相比，这种电容式架构有一些优点：

它提供了更好的噪声与功率权衡，因为它包含的噪声源更少。与电阻相比，需要的放大器更少，电容不会产生噪声。

与电阻器相比，电容器具有广泛的优势。除了无噪音外，它们不会受到自发热的影响，并且通常提供更好的匹配和温度漂移。这对失调、增益误差和漂移规格有积极影响。

电容将输入共模与信号链共模的其余部分去耦。这在CMRR、PSRR和THD方面具有优势。

最强大的优势之一是容性PGA输入共模范围可以是轨到轨甚至更高。这样就可以将传感器共模电压偏置到从正电源轨到负电源轨的几乎任何地方。

这种电容式架构结合了仪表放大器的优点，由于其输入是电容器，因此它具有非常高的输入阻抗。与作为增益元件的电阻相比，电容器的另一个优点是放大器的动态范围增加，不仅在信号摆幅方面，而且在噪声效率方面。

克服阻性PGA共模限制的常见解决方案是增加或移动电源轨，或者将传感器信号共模重新居中。这是以更高的功耗、电源设计复杂性、额外的外部元件和成本为代价的。

实例

在惠斯通电桥中，共模电压由连接在每个支路中的阻抗定义，并与施加的电源成正比。由于应变计中的线性检测优势，电子秤应用实现了这种检测拓扑，图8显示了II型半桥。

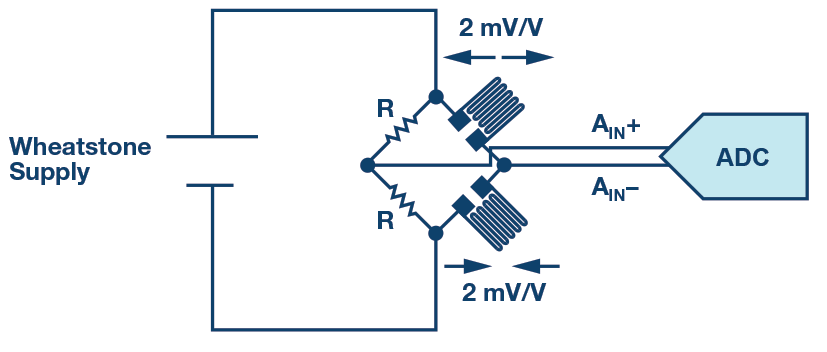
图8.惠斯通拓扑中带应变计的称重秤。

应变计的灵敏度通常为2 mV/V。惠斯通供应量越高，获得的灵敏度就越高。为了增加应变计的动态范围并最大化SNR，电桥的供电电源可能高于ADC。

在阻性PGA中，由于其共模限制，电桥应以与ADC电源相同的电源电压供电，以最大化动态范围，而在容性PGA中，电桥的供电几乎是ADC电源电压的两倍，因为没有输入共模限制。

例如，假设标准电源电平并以3.3 V电压为ADC供电，则在相同选定增益下，容性PGA优于阻性PGA的改进可总结为表1。

表 1.假设标准电源和增益的惠斯通电桥中阻性和电容性PGA的比较

 

职业高尔夫球协会	电阻式PGA	电容式PGA
最大惠斯通供应量	3.3 伏	6 V
应变计差分灵敏度	3.3毫伏	6 mV
动态范围改进 （dB）		5.2分贝

 

另一个可能的问题是，当电桥与ADC保持一定距离时，接地之间的电位差。这可能会改变共模电压，使ADC输入共模相对于电桥不平衡，并降低阻性PGA中的最大允许增益。

将容性PGA性能与阻性PGA相匹配的一种可能方法是在更高的电源电压下为电桥供电。例如，使用双极性电源（±3.3 V）为电桥供电，以提高应变计的灵敏度，但会增加系统复杂性和功耗。

另一个可以从电容式PGA中受益的例子是使用电阻温度检测器（RTD）或热电偶进行温度测量。

常用的RTD电阻（如PT100）可用于直接或间接检测热电偶冷端的温度，如图9所示。

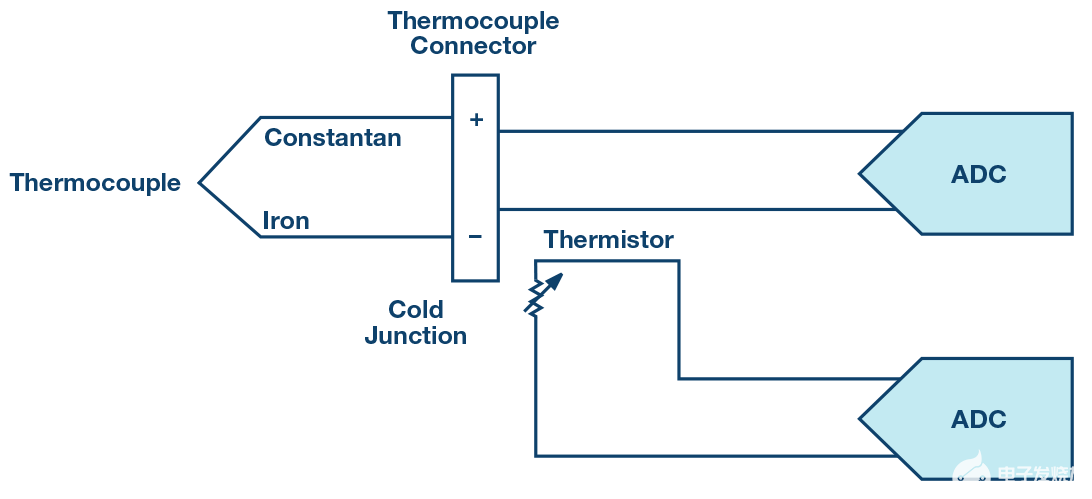
图9.典型的热电偶设置。

PT100 为每个元件提供不同的导线，是最受欢迎和最具成本效益的 3 线配置。

图10提出了一种在消除导联误差的同时测量温度的传统方法。在本例中，带PGA的Σ-Δ型ADCAD7124-8的内部电流源以相同的电流驱动RTD的两根导线，从而在两根引线上产生相等且与引线电阻成比例的失调误差。

由于引线电阻值小，AD7174-8提供的电流将自发热效应降至最低，RL3中产生的失调电压接近负供电轨，大大降低了阻性PGA的最大允许增益，因为其输入共模也将非常接近供电轨，而电容PGA则在内部将共模电压设置为电源轨的一半， 允许更高的增益配置，从而增加整体动态范围。

所提出的解决方案显著降低了系统和硬件连接的复杂性，因为第三根电缆不应返回到ADC PCB，并且可以连接到RTD位置附近的地。

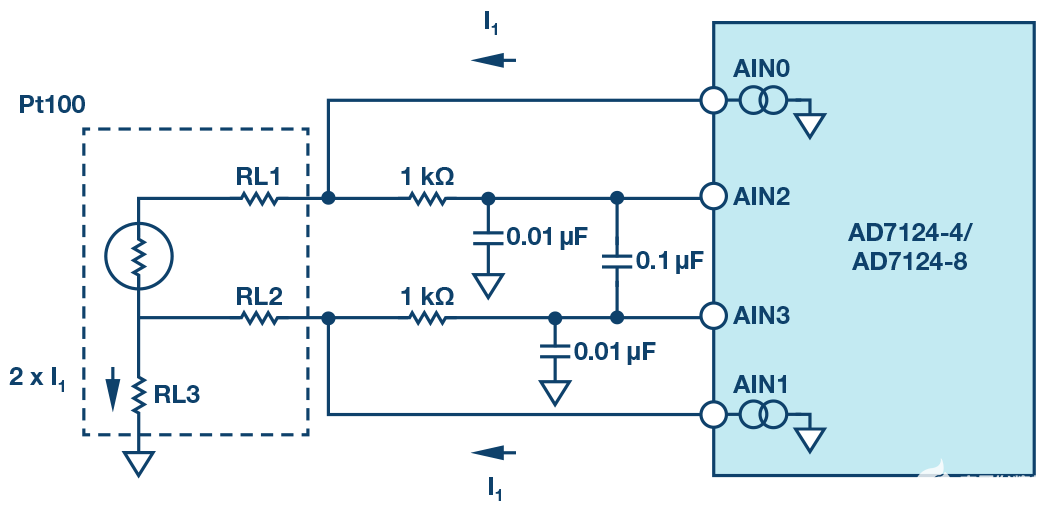
图 10.3线RTD测量。

为了提高温度测量的精度，首选4线测量。在这种情况下，仅使用一个电流基准。为了避免电流源的不精确性，可以使用比例测量和精密电阻作为ADC基准电压发生器，如图11所示。

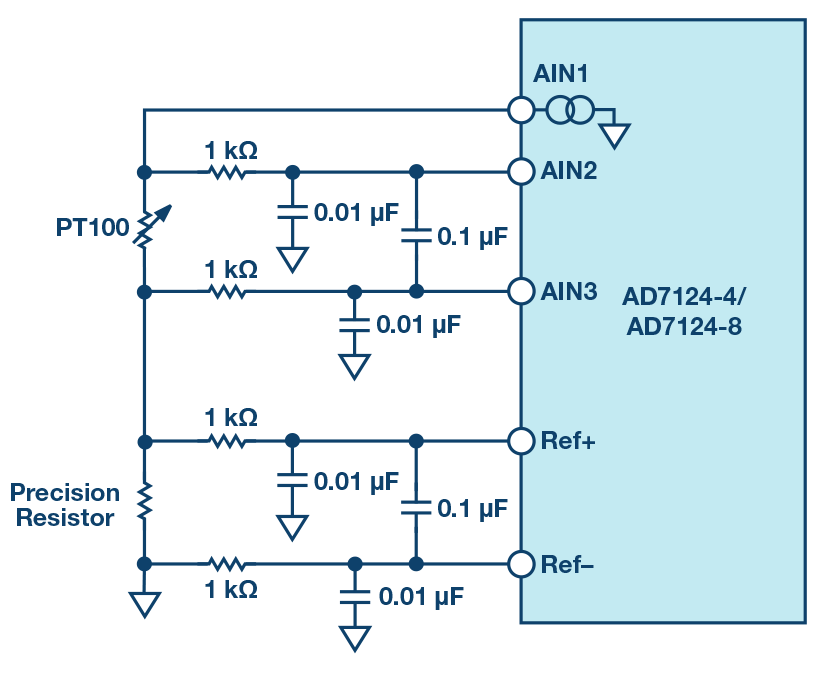
图 11.比率式 4 线 RTD 测量。

选择外部精密电阻的值，使RTD两端产生的最大电压等于基准电压除以PGA增益。

对于3.3 V电源，在阻性PGA中，精密电阻上产生的电压应在1.65 V左右，否则PGA共模电压将限制最大增益。结果是最大增益信号应等于1.65 V。在容性PGA中，没有输入共模限制，因此，RTD共模信号可以靠近顶轨，从而使精密电阻产生的ADC基准电压最大化，从而可以最大化最高的可选增益和动态范围。

表2总结了阻性PGA相对于容性PGA的最大增益，最大电流源为500 μA，以限制Pt100自发热，假设B类RTD，最高温度为600°C，最大VREF为2.5 V。

表 2.4线RTD比率测量中阻性和电容性PGA的比较

 

职业高尔夫球协会	电阻	电容的
Pt100 输出电压	500 μA × 313.7 = 156.85 mV	500 μA × 313.7 = 156.85 mV
VREF	1.65 伏	2.5 伏
最大PGA增益	1.65 V/156.85 mV ≈ 11	2.5 V/156.85 mV ≈ 16
改进（分贝）		3.6

 

结论

与阻性PGA相比，电容式PGA具有许多重要优势。由于作为增益元件的电容器固有的温度稳定性和匹配特性，噪声、共模抑制、失调、增益误差和温度漂移等关键规格得到了改善。

另一个关键特性是输入共模电压与放大器内部共模电压的去耦。当要放大的输入信号位于接近供电轨的共模电压上时，这一点至关重要。阻性PGA选择增益将受到其共模限制的严重限制，或者需要更高的电源轨或外部元件将输入信号重新偏置到电源轨的一半。相反，电容式PGA可以轻松处理这种传感场景。

审核编辑：郭婷