关于模拟噪声分析的11个误区

噪声是模拟电路设计中的一个中心主题，直接影响从测量中提取多少信息以及获得所需信息的经济性。不幸的是，存在大量关于噪声的混淆和错误信息，这可能导致性能不佳、代价高昂的过度设计或资源使用效率低下。本文探讨了模拟设计中噪声分析的11个最持久的误区。

1. 降低电路中的电阻值始终可以提高噪声性能

众所周知，根据约翰逊噪声方程，噪声电压随电阻值的增加而增加，这是一个众所周知的关系，e有效值= √4kTRB，其中 e有效值是均方根电压噪声，k是玻尔兹曼常数，T是以开尔文为单位的温度，R是电阻，B是带宽。这导致许多工程师得出结论，为了降低噪声，应该减小电阻值。虽然这通常是正确的，但不能假设，因为有一些特定的例子表明较大的电阻可以改善噪声性能。例如，在大多数情况下，电流是通过电阻器通过并测量产生的电压来测量的。根据欧姆定律，产生的电压与电阻值成正比，V = I × R，但如上所示，电阻的约翰逊噪声与电阻值的平方根成正比。由于这种关系，电阻值每加倍，信噪比就会提高3 dB。这种趋势一直持续到产生的电压过大或功耗过高。

2.所有噪声源的噪声谱密度可以相加，计算结束时可以考虑带宽

将多个噪声源的噪声频谱密度（nV/√Hz）组合在一起（电压噪声源组合为平方根和）可以节省时间，而不是单独计算每个噪声源的均方根噪声，但这种简化仅适用于每个噪声源看到的带宽相同的情况。如果每个噪声源看到的带宽不同，它就会成为一个危险的陷阱。图1显示了过采样系统的含义。从噪声频谱密度来看，增益放大器将主导系统的总噪声，但一旦考虑带宽，每级贡献的均方根噪声非常相似。

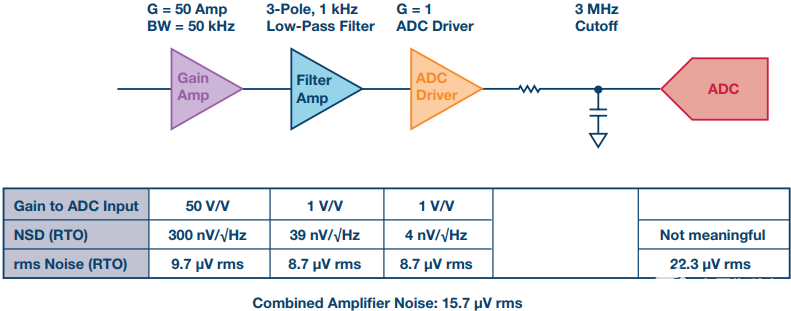
图1.使用均方根噪声而不是频谱密度进行噪声计算的理由。

3. 在手动计算中包括每个噪声源非常重要

在设计中考虑每个噪声源可能很诱人，但设计人员的时间是宝贵的，这在大型设计中可能非常耗时。全面的噪声计算最好留给仿真软件。但是，设计人员如何简化设计过程中所需的手噪计算呢？忽略低于特定阈值的次要噪声源。如果噪声源1/5e有效值主要噪声源（或参考同一点的任何其他噪声源）的值，它对总噪声的贡献小于2%，可以合理地忽略。设计师争论在哪里绘制阈值，低于该阈值就没有必要考虑噪声源，而是该水平是否1/3,1/5或1/10（分别增加了总噪声的5%、2%和0.5%），在设计足够固定以完全仿真或计算之前，不值得担心比这更小的噪声源。

4. 选择噪声仅为ADC噪声1/10的ADC驱动器

模数转换器（ADC）数据手册可能建议使用低噪声ADC驱动放大器驱动模拟输入，该放大器具有类似1/10ADC的噪声。但是，这并不总是最佳选择。在系统中，通常值得从系统级考虑ADC驱动器噪声的权衡。

首先，如果ADC驱动器之前的系统中的噪声源远大于ADC驱动器噪声，则选择噪声极低的ADC驱动器不会带来任何系统优势。换言之，ADC驱动器噪声应与系统其余部分相称。

其次，即使在只有一个ADC和一个放大器驱动它的简单情况下，检查噪声权衡并确定对系统的影响仍然可能是有利的。其原因可以通过数值示例更清楚地说明。考虑一个系统，该系统使用16位ADC，SNR值相当于100 μV rms噪声，以及10 μV rms噪声的放大器作为ADC驱动器。将这些源组合为平方根和时，总噪声为100.5 μV rms，非常接近ADC的单独噪声。可以考虑以下两个使放大器和ADC更接近平衡的选项，以及对系统性能的影响。如果将16位ADC替换为类似的18位ADC，其SNR相当于40 μV rms噪声，则总噪声将变为41 μV rms。或者，如果保留16位ADC，但将驱动器替换为功耗较低的放大器，该放大器产生30 μV rms噪声，则总噪声将为104 μV rms。与原始组合相比，这些权衡之一可能是更好的系统性能选择。这只是评估权衡及其对整个系统的影响的问题。

5. 在直流耦合电路中必须始终考虑1/f噪声

1/f噪声对极低频电路构成威胁，因为它无视许多常见的噪声抑制技术，如低通滤波、平均和长积分。然而，许多直流电路以白噪声源为主，以至于计算1/f噪声没有用，因为它不会增加总噪声。要看到这种效果，请考虑具有1/f噪声转折点f的放大器。数控，在 10 Hz 和 10 nV/√Hz 的宽带噪声下。计算10秒采集中的噪声，用于计算具有和不使用1/f噪声的各种带宽，以确定将其排除在外的影响。在这种情况下，当带宽为100倍f时，宽带噪声开始占主导地位数控，当带宽超过1000倍f时，1/f噪声不显著数控.良好的现代双极性放大器的噪声角可能远低于10 Hz，而零漂移放大器几乎完全消除了1/f噪声。

 

带宽（赫兹）	带宽/英尺数控	宽带 （nV rms）	1/f 噪声 （nV 均方根）	总噪声（ nV rms）	由于 1/f 而增加
100	10	100	220	240	140%
300	30	170	250	310	77%
1000	100	320	290	430	36%
3000	300	550	330	640	16%
10000	1000	1k	360	1.1k	6%
30000	3000	1.7千米	400	1.8千米	3%
100000	10000	3.2k	440	3.2k	1%

 

6. 由于1/f噪声在较低频率下增加，因此直流电路具有无限噪声

尽管直流是电路分析的有用概念，但事实是，如果认为直流在0 Hz下工作，那么实际上没有这样的事情。随着频率越来越低，接近0 Hz，周期变得越来越长，接近无穷大。这意味着即使在理论上响应直流的电路中，也可以看到最小频率。该最小频率取决于采集的长度或孔径时间，即监视设备输出的时间。如果工程师打开设备并观察输出 100 秒，他们可以观察到的最低频率伪影将是 0.01 Hz。这也意味着在这种情况下可以观察到的最低频率噪声也是0.01 Hz。

为了通过数值示例进行扩展，请考虑一个直流至1 kHz电路，其中输出受到连续监控。如果在电路的前100秒内观察到一定量的1/f噪声，从0.01 Hz到1 kHz（5个十倍频程的频率），那么30年内观察到的噪声量，即大约1 nHz（12个十倍频程），可以计算为√12/5 = 1.55，或比前100秒观察到的噪声多55%。这种有点平庸的增加甚至假设了最坏的情况：1/f噪声继续增加到1 nHz，到目前为止，还没有测量到的证据。理论上，当孔径时间定义不明确时，1/f噪声可以计算到在电路使用寿命期间等于1的频率。实际上，这些很长的时间线变化主要是由老化效应和长期漂移而不是1/f噪声主导的。许多工程师为直流电路中的噪声计算设置了最小频率，例如0.01 Hz或1 mHz，以保持计算的实用性。

7. 噪声等效带宽是噪声的乘数

噪声等效带宽（NEB）是噪声计算的有用简化。来自电路带宽之外的一些噪声能够进入电路，因为高于截止频率的增益不为零。NEB是计算出的理想砖墙滤波器的截止频率，该滤波器将允许与实际电路相同的噪声量。NEB大于–3 dB带宽，并且已针对常见滤波器类型和阶数进行了计算，例如，它比1极点低通滤波器或方程形式的NEB的–3 dB带宽大1.57×1 极= 1.57 ×带宽3分贝.然而，对于在噪声方程中放置乘法因子的位置，似乎一直存在混淆。请记住，NEB 是对带宽的调整，而不是噪声的调整，因此它位于平方根之下，如下所示：

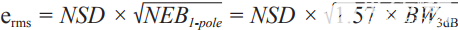
8.电压噪声最低的放大器是最佳选择

选择运算放大器时，电压噪声通常是设计人员考虑的唯一噪声规格。重要的是不要忽视当前的噪声。除输入偏置电流补偿等特殊情况外，电流噪声通常是输入偏置电流的散粒噪声：我n= √2 × q × 我B.电流噪声通过源电阻转换为电压，因此当放大器输入前面有一个大电阻时，电流噪声可能比电压噪声贡献更大。电流噪声成为问题的典型情况是，当低噪声运算放大器与输入串联时具有大电阻。例如，考虑低噪声运算放大器ADA4898-1，其10 kΩ电阻与输入串联。ADA4898-1的电压噪声为0.9 nV/√Hz，10 kΩ电阻的电压噪声为12.8 nV/√Hz，2.4 pA/√Hz电流噪声乘以10 kΩ电阻为24 nV/√Hz，是系统中最大的噪声源。在这种情况下，电流噪声占主导地位，通常可以找到电流噪声较低的器件，从而降低系统的噪声。对于精密放大器尤其如此，但也有高速FET输入运算放大器可以帮助高速电路。例如，与其选择ADA4898-1，也不想获得0.9 nV/√Hz电压噪声的优势，不如选择JFET输入放大器，如AD8033或ADA4817-1。

9. 在第一级获得大量增益可实现最佳噪声性能

通常建议在第一级采用增益以获得更好的噪声性能，这是正确的，因为与后续级的噪声相比，信号会更大。但是，获取增益的缺点是它减少了系统可以容纳的最大信号。在某些情况下，与其在第一级获得大量增益，这提高了测量的灵敏度，但限制了动态范围，不如限制第一级的增益量并以高分辨率进行数字化，以最大限度地提高灵敏度和动态范围。

10. 对于给定电阻，所有电阻类型都具有相同的噪声

电阻器的约翰逊噪声是基本噪声，从而产生特定电阻器在特定温度下的噪声的简单方程。然而，约翰逊噪声是电阻器中可以观察到的最少的噪声量，这并不意味着所有电阻类型都与噪声相同。此外，还存在过多的噪声，这是电阻器中1/f噪声的来源，与电阻器类型高度相关。过量噪声，有点令人困惑，也称为电流噪声，与电流在不连续介质中的流动方式有关。它被指定为噪声指数 （NI），以 dB 为单位，以 1 μV rms/V 表示直流每十年。这意味着如果有 1 V直流在NI为0 dB的电阻上，给定频率十进制内的多余噪声为1 μV rms。碳和厚膜电阻具有一些最高的NI，范围高达大约+10 dB，最好避免在信号路径的噪声敏感部分使用它们。薄膜电阻器通常在–20 dB左右要好得多，而金属箔和绕线电阻器可以低于–40 dB。

11. 如果采集足够多，平均可以无限期地降低噪声

平均被认为是一种通过平均值数的平方根来减少噪声的方法。当 NSD 持平时，这是有条件的。但是，这种关系在 1/f 范围和其他一些情况下中断。考虑在恒定频率f下采样的系统平均情况s，使得 n 个样本被 n 取平均值和抽取，并返回一些数字 m 抽取的样本。取 n 个平均值会将抽取后的有效采样率移动到 fs/n，将系统看到的有效最大频率降低 n 倍，并将白噪声降低 √n。但是，获得m个样本也需要n倍的时间，因此系统可以看到的最低频率也降低了n倍（请记住，没有0 Hz这样的东西）。取的平均值越多，这些最大和最小频率在频带上的移动就越低。一旦最大和最小频率都在1/f范围内，总噪声仅取决于这些频率的比值，因此增加平均值的数量不会对噪声产生进一步的好处。对于多斜率等积分ADC，相同的逻辑也适用于较长的积分时间。除了这个数学练习之外，还有其他实际限制。例如，如果量化噪声是主要噪声源，使得具有直流输入电压的ADC的输出是没有闪烁的恒定代码，则任意数量的平均值都将返回相同的代码。

审核编辑：郭婷