

一种了解非理想效应对电机驱动电流环路影响的系统方法
描述
作者:Jens Sorensen and Dara O’Sullivan
任何数控电机驱动器的一个重要部分是相电流反馈。测量质量直接关系到系统参数,如转矩脉动和转矩建立时间。虽然系统性能与相电流测量之间存在很强的相关性,但很难转化为对反馈系统的硬要求。从系统角度出发,本文讨论如何设计针对电机控制优化的反馈系统。确定错误源并讨论缓解效果。
1. 简介
电机驱动器或伺服中的电流环路性能(见图1)直接影响电机的扭矩输出,这对于平滑响应以及准确的定位和速度曲线至关重要。平稳扭矩输出的关键衡量标准是扭矩脉动。这对于扭矩脉动直接转化为可实现的最终应用精度的仿形和切割应用尤其重要。与电流环路动力学相关的参数,如响应时间和建立时间,对于生产效率直接受可用控制带宽影响的自动化应用非常重要。除了电机设计本身,驱动器内的多个因素也会直接影响这些性能参数。
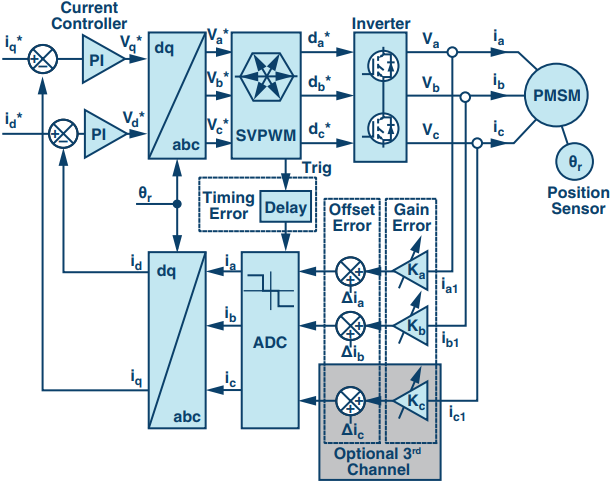
图1.电机驱动器中的电流环路,反馈路径中具有非理想元件。
电机驱动器中有多种扭矩脉动源。有些来自电机本身,例如由于定子绕组和槽布置以及转子电动势谐波引起的齿槽转矩。1转矩脉动的其他来源与相电流反馈系统中的失调和增益误差有关2(见图1)。
逆变器死区时间也直接影响转矩脉动,因为它增加了低频(主要是5吨)h和 7千)3定子电频率的谐波分量为PWM输出电压。在这种情况下,对电流环路的影响与电流环路在谐波频率下的干扰抑制有关。
本文将重点介绍相电流测量引起的转矩纹波。分析了每个误差,并讨论了最小化测量误差影响的方法。
2. 电流测量误差引起的转矩脉动
三相永磁电机的电磁转矩方程为:
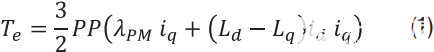
Te是电磁转矩,PP是极对数,λ下午是永磁磁通量,Ld和Lq是同步旋转参考系中的定子电感,以及我d和我q是同步旋转参考系中的定子电流。在稳态和理想条件下,我d和我q是直流量,因此,产生的扭矩也将是直流量。当有交流分量时,会出现转矩脉动我d或我q.因为 i 之间的直接关系DQ以及产生的扭矩 本文中使用的方法是分析各种测量误差如何影响我d和我q.作为此分析的基础,请考虑三相电机的电流反馈:
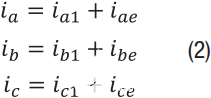
哪里我x是测量的相电流(x = a,b,c), ix1是实际相电流和我氙气是测量误差。不对错误的性质做出任何假设;它可以是失调、增益误差或交流分量。使用克拉克变换,电流被投射到静止的 两相量我α和我β:
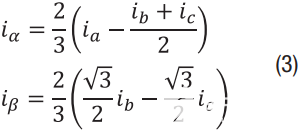
使用Park变换,将电流投影到旋转的两相量上我d和我q:
其中 θ 是转子的角度。对于三相电机的磁场定向控制,必须知道所有三相电流。一种常见的方法是测量所有三个电流,这自然需要三个传感器和三个反馈通道。另一种常见的方法是仅测量两个通道并计算第三个电流。出于成本和复杂性的原因,最好使用较少的传感器和测量通道,但正如将要解释的那样,测量所有三个电流会使系统对测量误差的鲁棒性更强。
2.1 两相测量
首先考虑具有两相电流测量的三相驱动器。第三相电流的计算假设电流之和为0。如果我一个和我b被测量,我c计算公式为:

使用公式(2)和(5):
在静止参考系中,电流为:
在旋转参考系中,电流为:
注意两者我d和我q有一个与真相电流相关的项和一个与测量误差相关的项(我DQ= iDQ1+ 我DQE).对于此分析,误差项我德和我量化宽松最感兴趣的是:
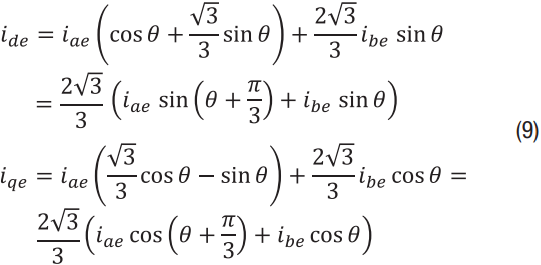
2.2 三相测量
现在考虑一个测量所有三相电流的三相驱动器。按照与两个通道相同的过程,得出静止量和旋转量:
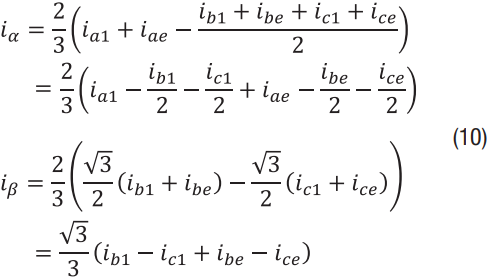
在旋转框架中:
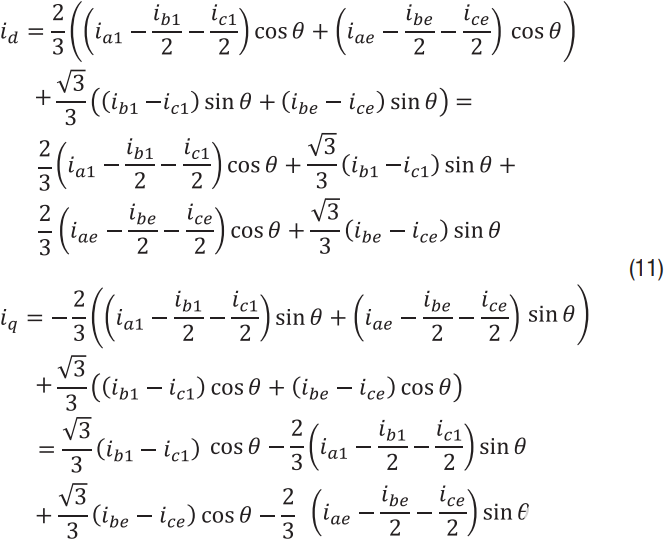
同样,方程有一个与真实相电流(iDQ1) 以及与测量误差相关的术语 (我DQE).错误项 i德和我量化宽松是:
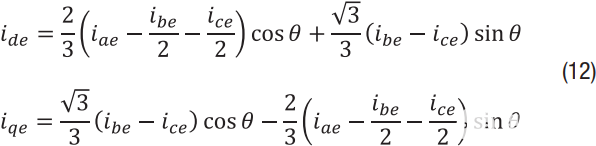
3. 采样即时不正确
当三相电机由开关电压源逆变器供电时,相电流可以看作是两个分量:基波分量和开关分量(见图2A)。
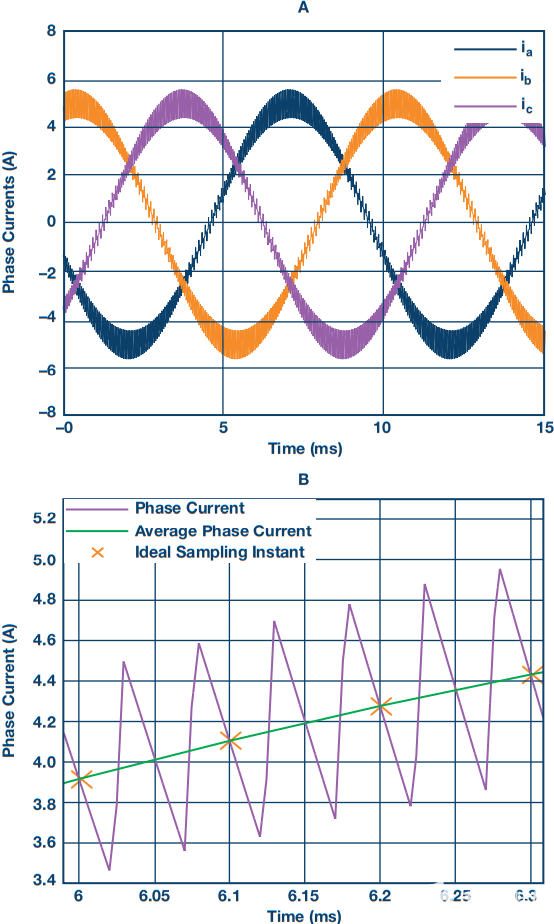
图2.(A) 由开关电压源逆变器驱动的三相电动机的相电流。(B) 相电流的变焦,说明电流纹波如何通过采样衰减。
出于控制目的,必须消除开关元件,否则会影响电流控制环路的性能。提取平均分量的常用技术是对与PWM周期同步的电流进行采样。在PWM周期的开始和中心,电流取平均值,如果采样与这些实例紧密同步,则开关分量被有效抑制,如图2B所示。但是,如果电流采样时出现时序误差,则会发生混叠,从而导致电流环路性能下降。本节讨论时序误差的原因,对电流环路的影响,以及如何使系统对采样时序误差具有鲁棒性。
3.1 电机驱动器中的采样时序误差
由于相电流的基本分量通常在几十Hz范围内,电流环路的带宽在几kHz范围内,因此,很小的时序误差会影响控制性能似乎违反直觉。然而,由于只有相位电感来限制di/dt,即使是很小的时序误差也会导致明显的电流失真。例如,在5 mH电感上250 V持续1 μs,电流将改变50 mA。此外,假设系统使用满量程为10 A的12位ADC,则由于时序误差,ADC的较低4.3位将丢失。如将要显示的,丢失位是最好的情况。混叠还会导致反馈系统中的转矩纹波和增益误差。
采样时刻不正确的最常见原因是:
PWM和ADC之间的链路不足,无法在正确的时间采样。
缺乏足够的(两个或三个,取决于被测量的相数)独立的同步采样保持电路。
栅极驱动信号的传播延迟,这将使电机电压与PWM定时器同相。
通常,任何可能影响di/dt的因素都决定了不正确采样时刻的严重程度。当然,时序误差的大小很重要,但电机速度、负载、电机阻抗和直流母线电压等系统参数也会直接影响误差。
3.2 采样误差对系统性能的影响
使用推导方程,可以确定采样误差的影响。对于 2 相电流测量,假设我一个在理想时刻(我AE= 0) 和我b以延迟采样,导致我是 ≠ 0.在这种情况下,公式9定义的误差项为:
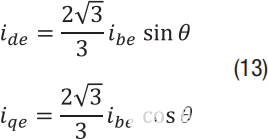
对于三相电流测量,假设我一个 和我c在理想的瞬间(我AE = 我公元= 0),ib 以延迟 (我是≠ 0)。在这种情况下,公式12定义的误差项为:
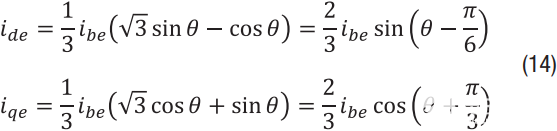
从等式13和14可以得出一些有趣的结论。首先,克拉克/帕克变换获得的测量误差不同:
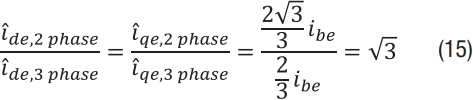
因此,如果反馈系统对其中一个电流测量有延迟,则对具有两个通道的驱动器的影响将比系统具有三个通道时高1.73倍。
使用公式13和14,还可以确定测量延迟对电机扭矩的影响。对于此分析,假设在向电机端子(V000或V111)施加零电压时对相电流进行采样,在此期间,驱动di/dt的唯一电压是BEMF。对于正弦 BEMF,di/dt 也将服从正弦函数——即 di/dt = 0 在 BEMF 零交叉时,di/dt 在 BEMF 达到峰值时最大。现在,如果相电流相对于理想采样时刻具有固定延迟进行采样,则误差为正弦:
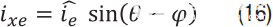
其中 x = a,b,c 和 φ 是相对于 dq 参考系的相位角。用我德 以公式13为例:
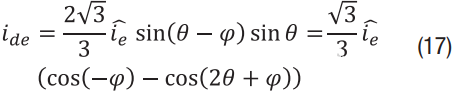
术语 cos(– φ) 是偏移量,而 cos(2 θ – φ) 是以基频两倍振荡的交流分量。在dq电流中使用这些分量时,电机转矩将具有类似的分量。需要注意的另一件事是,对于三次电流测量,dq帧的选定方向φ = –π,这意味着偏移项为零。也就是说,三个通道没有增益误差。双传感器和三传感器系统之间的差异如图3所示。
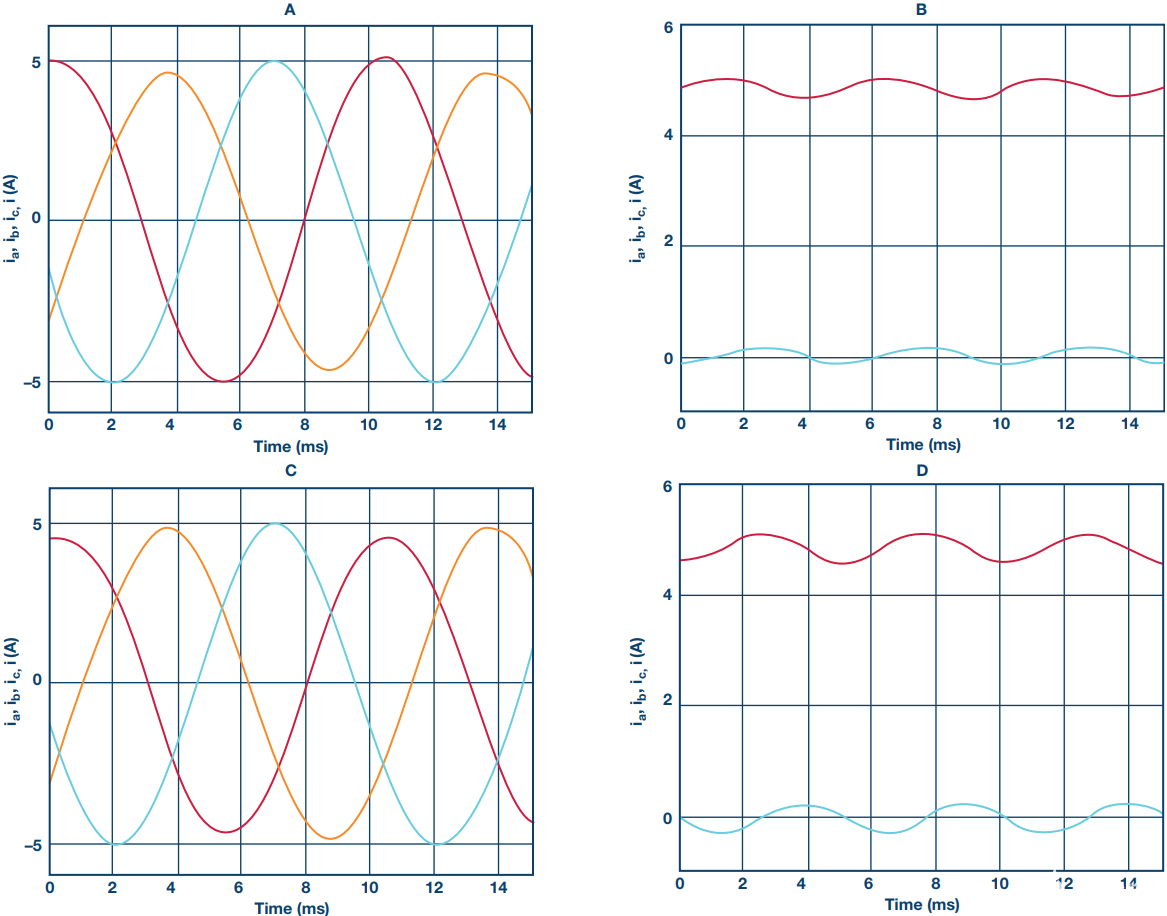
图 3:不正确采样时刻的影响。我一个我b我c和我d我q带有两个电流传感器(A、B)和三个电流传感器(C、D)。
在图 3A 和 3B 中的三个传感器案例中,请注意延迟如何我b测量结果是基频的 2 倍电流(转矩脉动)。另请注意 DC 组件如何我d和我q不受影响。
在图 3C 和 3D 中的两个传感器案例中,请注意延迟如何我b 测量结果的交流分量比使用三个传感器高 1.73 倍。此外,两者的直流分量我d 和智商也受到影响。
3.3 最小化效应采样时序误差
随着控制环路性能要求的提高,最好将采样时序误差的影响降至最低,尤其是在考虑到ADC分辨率提高的趋势时。几年前,10至12位ADC很常见,但现在16位分辨率正在成为常态。应利用这些额外的位,否则高性能ADC的值将因系统延迟而损失较低的位而受到影响。
最小化采样时序误差影响的最有效方法是尽可能接近所有相位的理想采样时刻。这可能会导致选择针对数字控制开关电源转换器优化的控制器。此外,优化栅极驱动电路中的传播延迟/偏斜将产生积极影响。
如果时序误差最小化仍然不能满足要求,则使用三个电流传感器和一个具有三个独立采样保持电路的ADC可以实现显著的性能改进。
4. 失调误差
推导的方程还可以描述系统如何对测量电流的偏移做出反应。首先,通过查看两个传感器外壳并使用我德以公式9为例,误差分量可以表示为:
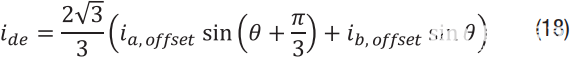
跟我a,偏移和我b,偏移量分别为 A 和 B 通道的偏移。可以看出,偏移将导致电流中的交流分量(和 扭矩)在电机的基频下。如果系统在启动时进行了失调校准,则任何剩余的失调都将是由于漂移造成的。在这种情况下,假设传感器以相同的方式漂移,则近似值我a,偏移 = 我b,偏移量 =我抵消可以制作。
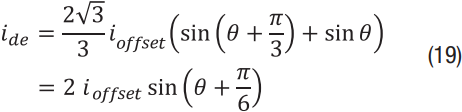
这意味着误差分量的幅度是相位偏移幅度的两倍。对于误差电流的q轴分量,也可以找到类似的结果。使用三个电流传感器执行相同的练习,发现我德 公式 12 为:
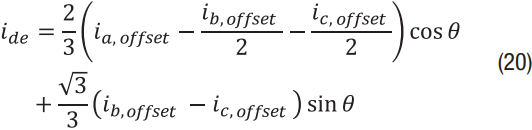
根据初始偏移被校准并且所有传感器漂移相等的推理,我a,偏移= ib,偏移量= ic,偏移= i抵消:
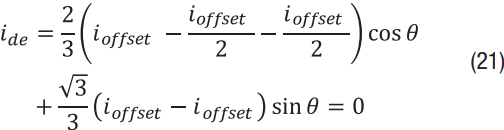
同样,拥有三个传感器的好处是显而易见的——电流传感器上的偏移不会受到转矩脉动的影响。即使传感器的漂移方式不完全相同,它们也可能表现出相同的趋势。因此,在具有未校准失调误差的系统中,三传感器设置将始终具有显着较低的转矩脉动。
4.1 最小化失调误差的影响
电流反馈偏移是电机驱动器中转矩脉动的主要来源之一,希望尽可能将其降至最低。一般来说,电流反馈有两种类型的失调误差。首先,在任何时间点和任何温度下都存在静态偏移。其次,失调漂移是温度和时间等参数的函数。将静态失调的影响降至最低的常用技术是进行失调校准,可以在制造时或每次电机电流为0时(通常在电机停止时)进行。如果使用这种方法,静态偏移通常不是问题。
失调漂移处理起来更复杂。由于这是通常在电机运行时发生的缓慢漂移,因此很难进行在线校准,并且通常不能选择停止电机。已经提出了一些基于观察者的在线校准技术,4但观察者依赖于电机的电气和机械系统模型。为了使在线估算有效,需要对电机参数有准确的了解,而通常情况并非如此。
如前所述,最有效的失调漂移缓解方法是使用三种电流测量。假设通道使用相同类型的组件,则通道的漂移可能相似。如果是这种情况,偏移会抵消,并且不会导致转矩脉动。即使通道不以相同的速率漂移,只要它们沿同一方向漂移,三通道方法也会对偏移产生抵消作用。
通过两次电流测量,即使通道以相同的速率漂移,转矩脉动也存在。换句话说,双传感器系统对失调漂移非常敏感。在这种情况下,避免转矩脉动的唯一方法是确保漂移保持在较低水平,这可能会增加反馈系统的成本和复杂性。对于一组给定的性能要求,3通道反馈系统可能被证明是具有成本效益的解决方案。
5. 增益误差
当系统在电流反馈、误差信号、我氙气,与实际相电流成正比,我x1(x = a, b, c):
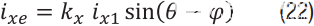
这是基频处的正弦误差。可以看出,增益引起的误差性质与采样时序不正确引起的误差相似(参见公式16)。因此,可以得出同样的结论:
如果所有通道上都存在相同的增益误差,则不会有转矩纹波;只有增益误差。这适用于 2 通道和 3 通道系统。
如果增益误差因通道而异,则会导致基频两倍的转矩纹波分量。
2通道电流测量对增益误差的敏感度是3通道电流测量的1.73倍。
6. 实验验证
失调误差和增益误差对测量电流和输出转矩的影响在图4所示的实验设置中得到了验证。
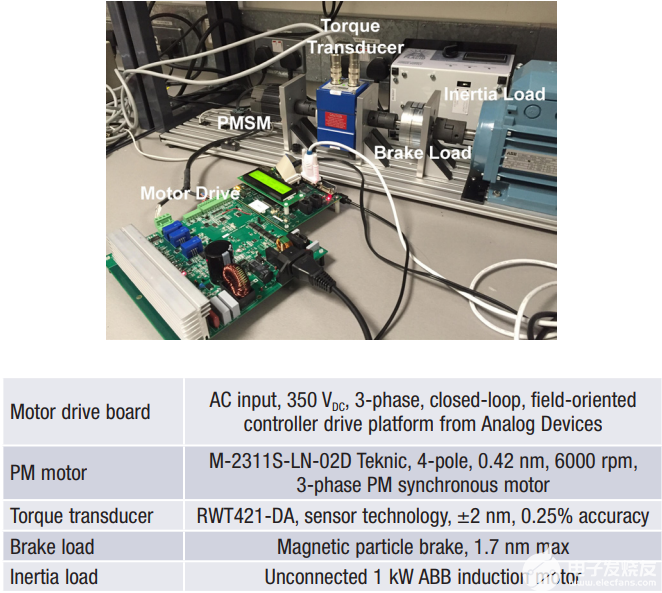
图4.测试台设置。
驱动板中的电流反馈电路在三个电机相位中使用霍尔效应传感器。可以在软件中选择 2 相或 3 相电流测量。失调校准是在电机不运行时执行的,因此在正常工作(不留时间产生漂移效应)下,失调和增益误差非常小。为了说明这些误差的影响,这些误差通常是由于温度漂移而存在的(尽管有校准程序),在校准程序之后,控制软件中引入了人为的失调和增益误差。控制算法看到的测量数量将与实际数量不同,实际数量将包含前面各节中讨论的误差的影响。图 5 说明了设定转速参考为 520 rpm 时的情况,因此电机电频率为 35 Hz。
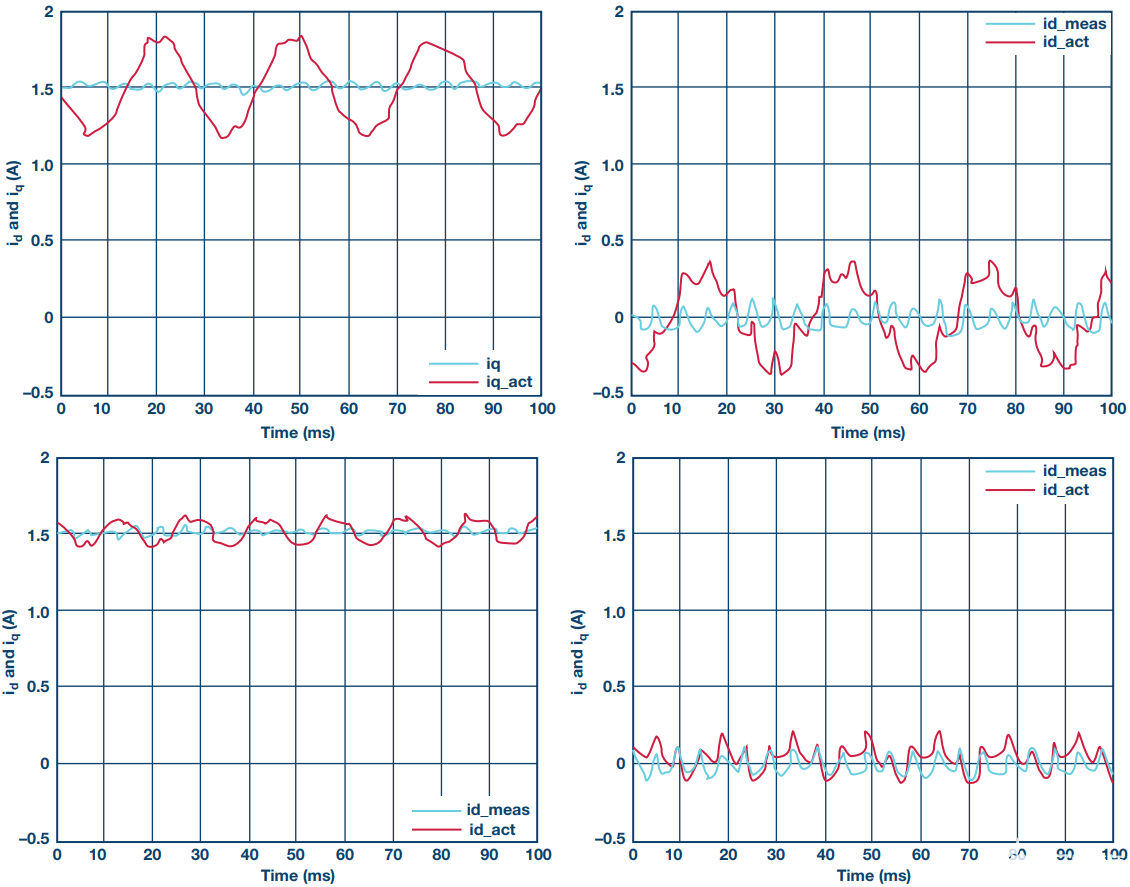
图5.实际(红色)和测量(蓝色)(从上到下);我q和我d具有1%的失调误差;我q和我d具有非对称增益误差 (1.05/0.95)。
很明显,当驱动器将d轴和q轴电流控制在相对恒定的值以保持设定速度时,实际电流包含显着的谐波成分,特别是在失调误差的情况下。这些谐波分量直接影响输出转矩脉动。如图 6 所示。必须注意的是,由于试验台中的轻微轴不对中,存在显着的机械扭矩脉动。这存在于机械频率和一些低次谐波中。但是,仍然清楚地看到与失调和增益误差源相关的谐波含量变化。对于失调误差,如图所示,电频率(35 Hz)处的谐波分量与失调误差百分比成比例增加,而电频率两倍处的谐波成分随增益误差不对称性而增加,如理论预测的那样。
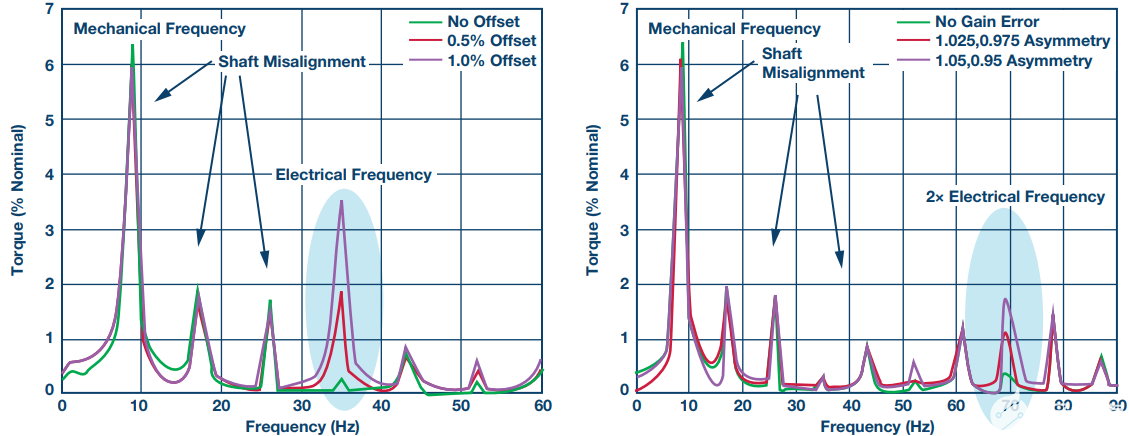
图6.通过两相电流测量测得的转矩纹波占标称值的百分比,(左)失调误差增加,(右)增益误差增加。
此外,图7清楚地显示了三相测量的影响,其中完全消除了失调误差引起的转矩纹波,增益误差引起的转矩纹波降低了1.73倍,再次证明了理论计算。
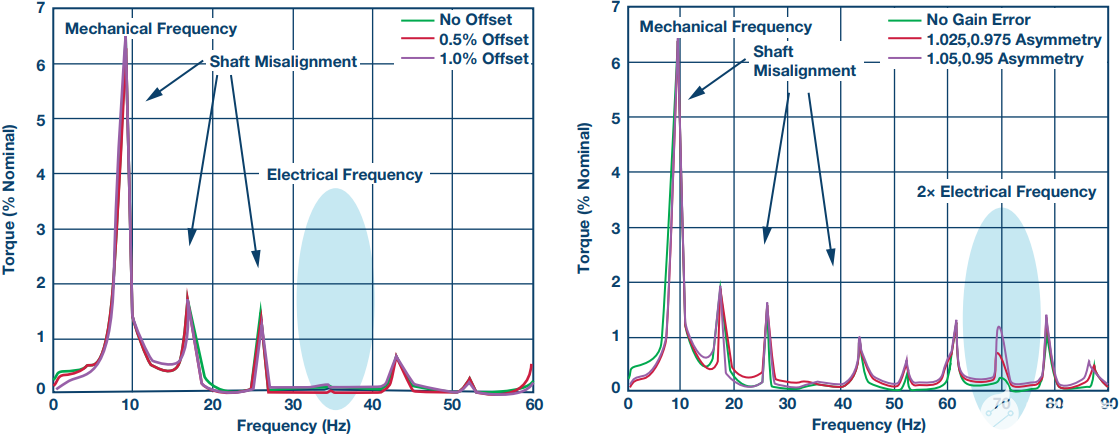
图7.通过三相电流测量测得的转矩纹波占标称值的百分比,(左)失调误差增加,(右)增益误差增加。
总结
通过分析和测量,本文展示了电流反馈系统中的非理想效应如何影响系统性能。已经表明,具有三个电流测量的系统比具有两个电流测量的系统在测量误差方面明显更可靠。
审核编辑:郭婷
-
为电机一体化应用提供一种大电流单通道集成电机驱动芯片2024-12-18 888
-
介绍一种扁线电机趋肤效应和邻近效应的新型解决方案2023-07-18 3127
-
网络突发环路你的应对方法是什么?2023-05-22 4451
-
PWM驱动有刷电机时的电流再生方法及其区别2023-02-24 2220
-
一种伺服电机的控制方法2021-09-03 2156
-
开发一种电机驱动控制系统面临哪些挑战?2021-06-17 1413
-
求一种应对压电效应失效的电容器解决方案2021-06-08 1906
-
新型非联网2.4GHz技术为什么会是一种理想的选择?2021-05-28 1306
-
电机驱动器电流环路中非理想效应影响的系统方法2018-10-18 2768
-
一种集成反馈环路的自举升压驱动电路设计_杨令2017-01-07 778
-
一种采用正弦电流环PWM驱动方法的混合式步进电机驱动装置及其在经2016-05-11 760
-
一种LED芯片非接触式在线检测方法2012-07-31 3797
-
一种斩波式电流型步进电机驱动电路方案2010-05-06 609
-
一种新型步进电机驱动电源的研制2010-01-10 459
全部0条评论

快来发表一下你的评论吧 !

