介绍导航坐标系与载体坐标系之间的姿态旋转矩阵

01 

说在前面的话 

在 MEMS 惯性传感器06 - 再说坐标系定义（导航坐标系与载体坐标系）这篇章中，在介绍导航坐标系与载体坐标系之间的姿态旋转矩阵使用的是用欧拉角表示旋转矩阵。

我们知道用来表示姿态的方法有： 1）欧拉角  2）方向余弦矩阵  3）四元数  4）等效旋转矢量。   本篇我们介绍采用四元数表示姿态矩阵。 以下内容摘抄 《惯性导航》- 秦永元 姿态更新计算的四元数算法章节。

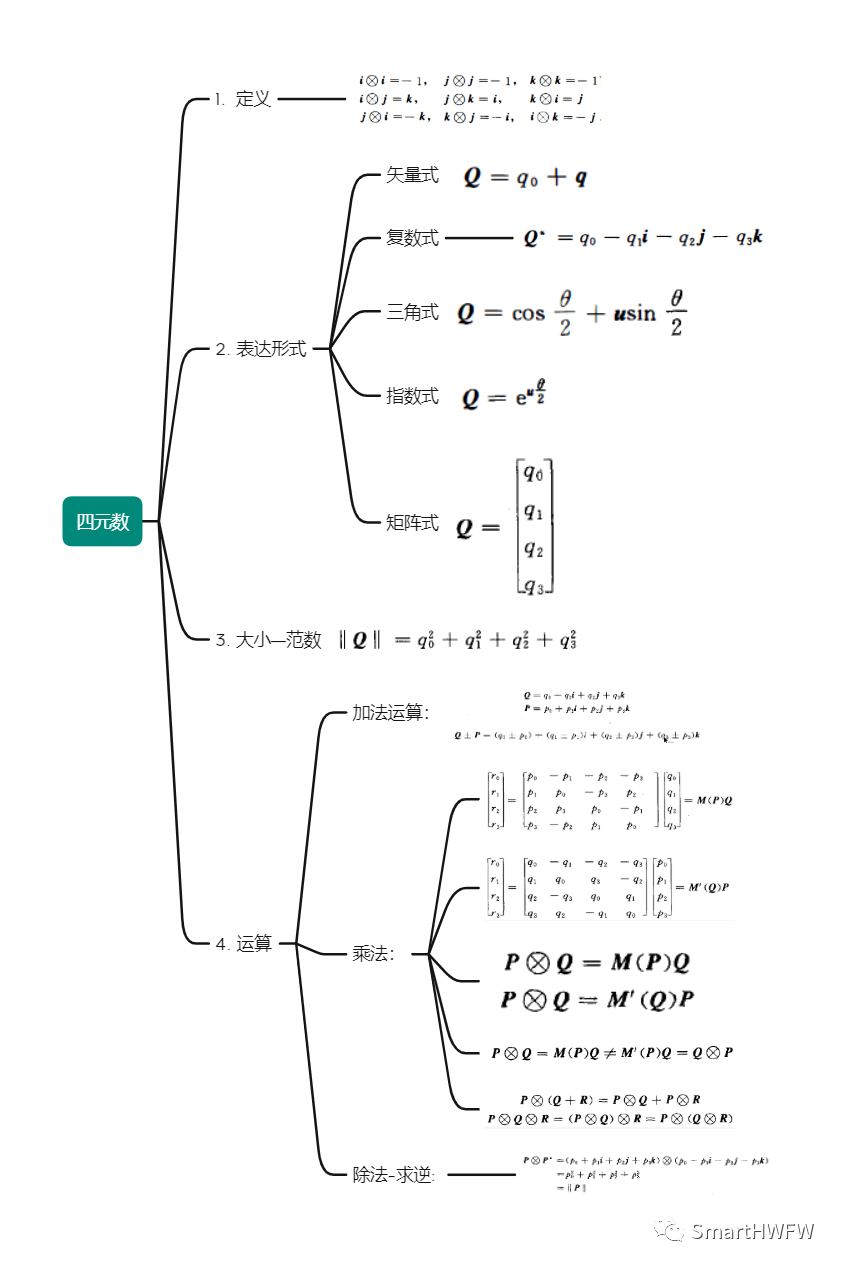
关于四元数的介绍和运算规则可以看前期文章。这里简单的汇总一下：

02 

 四元数表示矩阵 

三维空间的任意旋转，都可以用绕三维空间的某个轴旋转过某个角度来表示（即轴角，Axis-Angle表示方法）。这种表示方法里，Axis可用一个三维向量(x,y,z)来表示，θ可以用一个角度值来表示，直观来讲，一个四维向量(θ,x,y,z)就可以表示出三维空间任意的旋转。    

注意，这里的三维向量(x, y, z)只是用来表示axis的方向朝向，因此更紧凑的表示方式是用一个单位向量来表示方向axis，而用该三维向量的长度来表示角度值θ。这样，可以用一个三维向量(θx, θy, θ*z)就可以表示出三维空间任意的旋转，前提是其中(x,y,z)是单位向量。这就是旋转向量(Rotation Vector)的表示方式。  

Axis-Angle的表示方法还可以推导出另一种很常用的三维旋转表示方法，叫四元数(Quaternion)。同上，假设(x, y, z)是axis方向的单位向量，θ是绕axis转过的角度，那么四元数可以表示为 [cos(θ/2), xsin(θ/2), ysin(θ/2), z*sin(θ/2)]。  

注意，这里可以推导出，用于表示旋转的四元数向量也必须是单位向量。四元数的神奇之处在于，对于三维坐标的旋转，可以通过四元数乘法直接操作，与上述旋转矩阵操作可以等价，但是表示方式更加紧凑，计算量也可以小一些。捷联惯导中的姿态更新实质上是如何计算四元数Q。  

审核编辑：刘清