开关电源环路补偿设计

ps：上篇讲述TL431的文章中有点小错误，现更正见下图。
 

1. 理论讲解

在上一篇文章中我们推导了TL431补偿器的2型传递函数，本文将讲述实际环路补偿的设计步骤。

对于硬件工程师来说，开关电源和运放的信号处理电路是最常遇到的，都是典型的带负反馈的闭环控制系统。因此，这两类电路设计的稳定性和控制理论密切相关。简化的闭环控制系统框图如图1所示，被控对象的传递函数为H，反馈部分的传递函数为G。

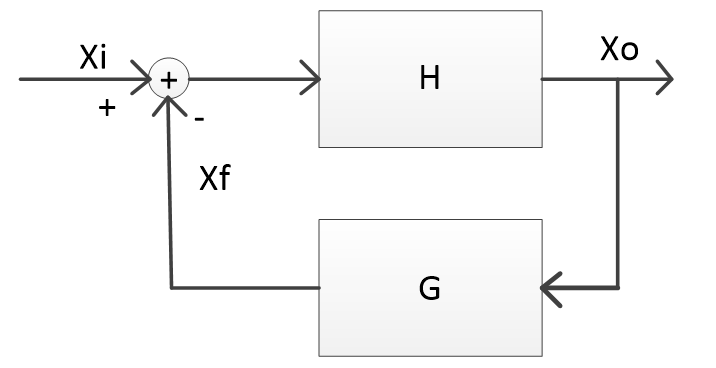
图1

以上各式中的GH一般称为系统的环路增益或者开环增益。

根据式（2）可知，当1+GH=0，即GH=-1时，意味着环路增益为1，相位滞后180°，系统不稳定发生自激振荡。当然也可以从另一个角度进行理解，系统发生自激振荡时，不需要输入量Xi，即净输入量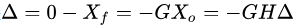，可得GH=-1，即反馈量Xf和输出量Xo形成彼此互相维持的关系。

从稳定性条件出发，我们可以知道环路增益小于1时系统可以稳定，相位滞后不到180°时系统可以稳定。这表明左半平面的极点和零点都在某一方面提升稳定性，另一方面降低稳定性。比如左半平面极点可以使增益降低，这能提升稳定性；但是极点增加了相位滞后，这降低了稳定性。比如左半平面零点使相位超前，这能提升稳定性；但是零点使增益增加，这降低了稳定性。只有右半平面零点是最特殊的，增加增益的同时相位滞后，这会加剧系统不稳定。

根据控制理论的稳定性条件可知，相位裕量至少为45°，转化为伯德图的话，就是要求在增益为0dB时的穿越频率处，斜率应该为-20dB/decade，即负20dB每十倍频，或斜率为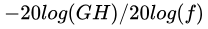，两者等价。

根据式（3）可知，当GH>>1时，即引入深度负反馈后，Xf=Xi。这就是为什么运放的虚短需要在引入深度负反馈时才成立的原因。由于运放本身的开环放大倍数H已经非常大，引入负反馈后一般都能满足深度负反馈的要求。

根据式（4）可知，如果想要直流稳态误差为0，则应满足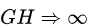。这就是为什么控制系统的低频环路增益（开环增益）要尽量大的原因，这点在开关电源环路设计中很重要。

对于一般的运放电路而言，图1即是其控制系统框图。而开关电源的系统框图则较为复杂，如图2所示，可以将PWM调制器，开关管和LC滤波器合并统称为功率级，用H表示，误差补偿器用G表示，反馈分压系数用k表示，实际设计中我们经常将k和G合并在一起称为G，则简化后的框图和图1类似，环路增益为GH。另外，实际系统中还经常存在输入扰动和负载扰动，通过线性叠加定理，总输出则可表示为下式：

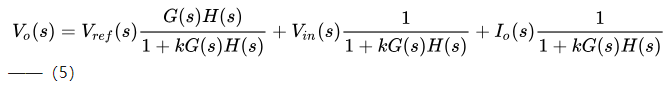
通过式（5）可以比较清楚地看到输入扰动和负载扰动对输出的影响，输入扰动对应线性调整率指标，负载扰动则对应负载调整率指标。另外通过前述结论我们知道，要想稳态误差越接近于0，则GH直流环路增益应该越大越好。

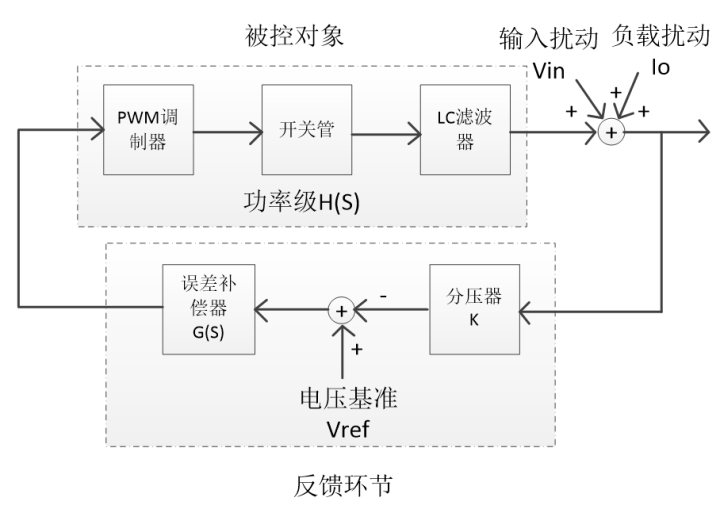
图2

以笔者平常设计中遇到最多的反激式开关电源为例，控制芯片采用的基本都是电流峰值模式。反激式开关电源是从buck-boost拓扑演变而来，拓扑示意如图3所示，该拓扑中所有参数为转化为到副边侧后的等效参数。

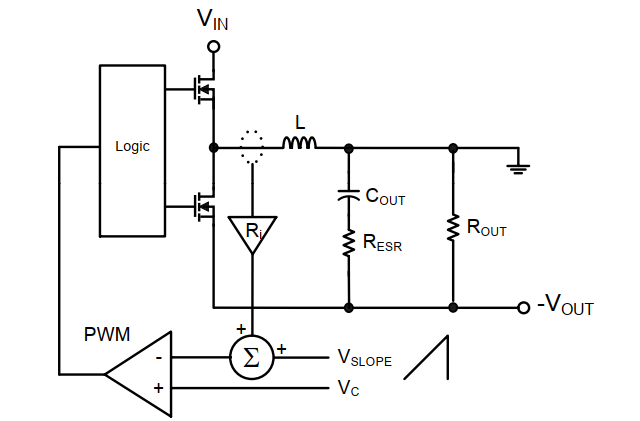
图3

电流模式的的功率级传递函数为：

 

 

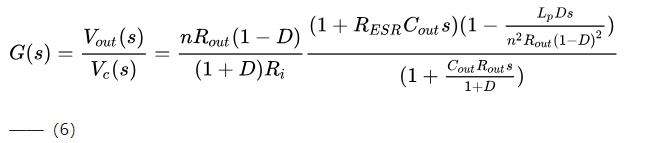
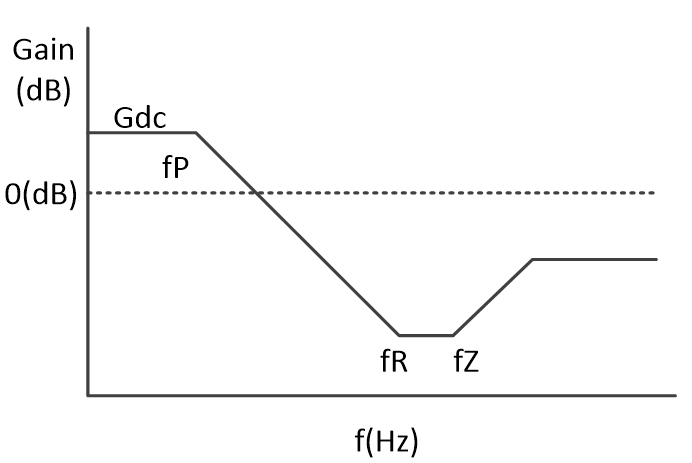
图4

在开头所说的文章中我们已经得到了使用TL431的2型补偿器传递函数，此例采用如图5所示的环路接法，其传递函数为：

 

图5

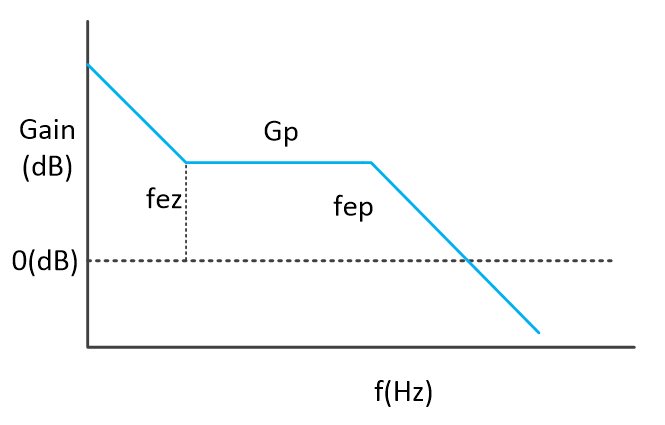
图6

将功率级传递函数和补偿器传递函数的伯德图进行相加叠加，就得到环路增益GH的伯德图，如图7中的橙色曲线所示。

图7

记补偿后的穿越频率为fc（即我们人为想要设置的截止频率，已知），补偿器传递函数的积分器部分的穿越频率为fp0，功率级传递函数的极点（补偿器传递函数的零点）为fp，补偿器的中频带增益为Gp，由于伯德图将传递函数从乘除关系转化为了加减关系，各曲线之间可以通过平移关系进行求解，因此可以推导得出以下结论：

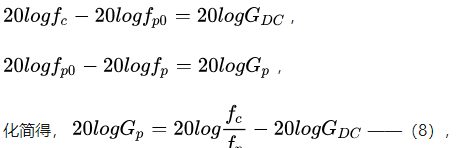
据此求得Gp大小。

当然以上所有推导都基于一个前提条件：电路工作于CCM（连续导通模式）。

设计实例

假设设计好完毕功率级的反激电源输出12V，1A（负载12Ω），轻载时电流为0.5A（负载24Ω），输入为220V市电，原边侧电感Lp=10mH，匝数比n=9.8，输出电容为470uF，其ESR=50mΩ，开关频率fs=55KHz，电流检测电阻Ri=1Ω，最大占空比D=0.45。

 

现在我们得到了式（9）（10）（11），根据上篇文章静态工作点的计算方法，假设算的R4=2K，R5=1K，光耦的CTR=1，R6=6K，由于输出12V，基准电压为2.5V，所以可选择R1=15K，R2=3.9K。

因此，根据式（9）可求得：R3=10K。

根据式（10）可求得：C1=14nF，选为15nF。

根据式（11）可求得：C=3.8nF，选为3.9nF。当然最后要根据电路板实测再进行参数调整。