RLC振荡原理详解 RLC振荡通俗解释

PS：由于本篇文章较长，为了不影响阅读体验，所以一分为二，本篇先讲述振荡原理，下一篇再讲实际的Snubber电路。

RLC谐振电路广泛应用于选频电路中，但由于本人从事非射频相关工作，所以实际接触的选频应用并不多。但是RLC阻尼振荡却在平时的电路设计中经常遇到，尤其是与各种电源场合相关的波形振荡、RC Snubber吸收电路等，其背后的本质都是RLC二阶电路动态响应过程的阻尼振荡。在之前的继电器和电源文章中都简单提及到过这个问题，本系列文章将进行详细讲述。

1. RLC振荡原理

常见的串联RLC和并联RLC电路，其原理类似相通，本文以串联RLC为例进行说明，但并不进行公式推导，而是从结论出发，与实际电路情况进行对应说明。

1.1 零输入响应

零输入响应的RLC电路如图1所示，初始条件为电容电压UC等于U0，电感电流I等于0，然后开关从左往右拨，根据电路参数的不同，零输入响应有四种情况：

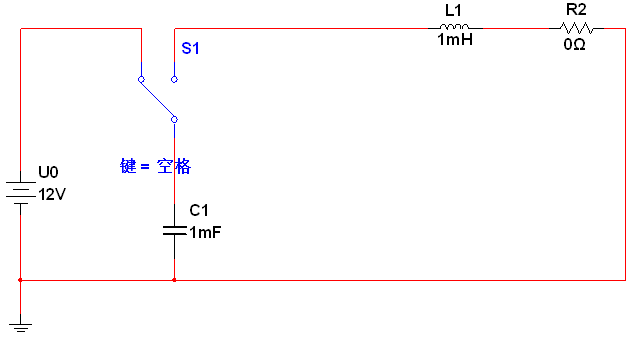
图1

（1）过阻尼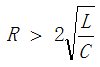，，电路中的电流在放电过程中永不改变方向，电容在全部时间内一直在非振荡放电，对应波形示意如图2所示；

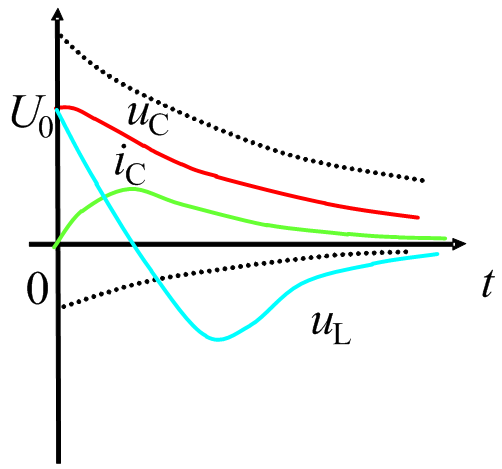
图2

（2）临界阻尼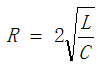，，电容非振荡放电，波形与过阻尼类似，如图2所示；

（3）欠阻尼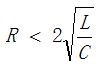，，电容电压在零值附近做衰减振荡放电，电流也在零值附近做衰减振荡，对应波形示意如图3所示。这三种有阻尼的情况下，振荡角频率为，

；

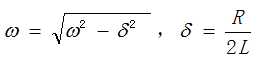
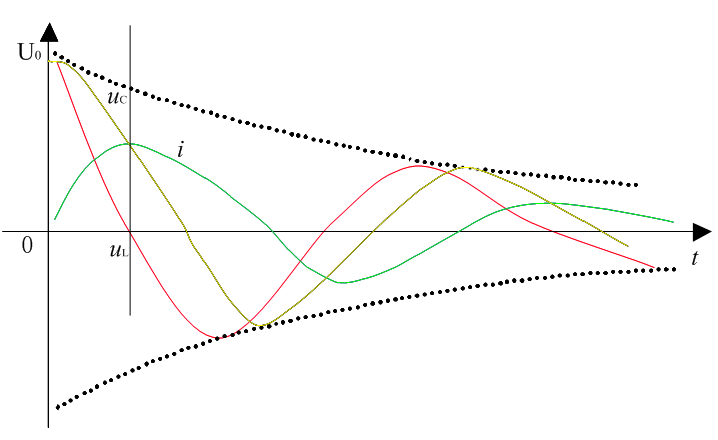
图3

（4）无阻尼，R=0，电容电压按正弦规律做等幅振荡，振荡角频率为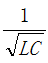，对应波形示意如图4所示，现实情况中阻尼R不可能为0，所以不存在这种现象。

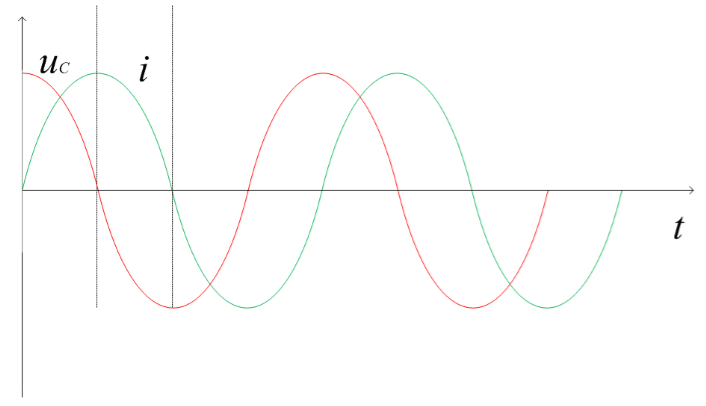
图4

1.2 零状态响应

零状态响应的RLC电路如图5所示，初始条件为电容电压UC和电感电流I均等于0，然后输入激励。与零输入响应类似，零状态响应也有四种情况：

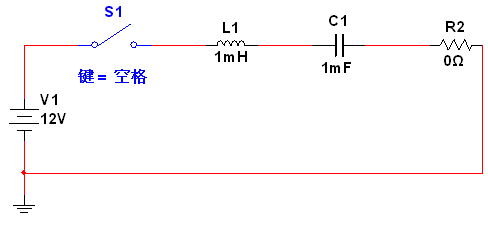
图5

（1）过阻尼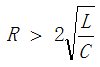，，电路中的电流在充电过程中永不改变方向，电容在全部时间内一直在非振荡充电，对应波形示意如图6所示；

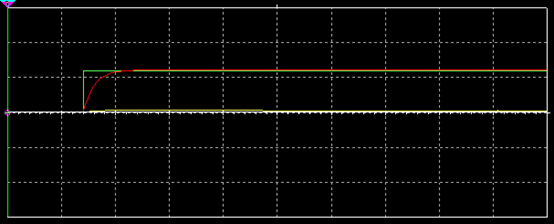
图6

（2）临界阻尼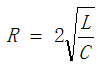，，电容非振荡充电，波形与过阻尼类似如图6所示；

（3）欠阻尼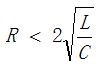，，电容电压在电源电压值U0附近做衰减振荡充电，但是不会超过电源电压的2倍，电流在零值附近做衰减振荡，对应波形如图7所示。这三种有阻尼的情况下，振荡角频率为

；

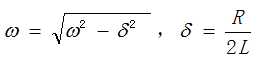
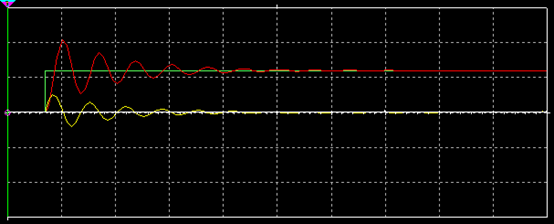
图7

（4）无阻尼，R=0，电容电压围绕着电源电压值U0按正弦规律在0~2倍的电源电压大小之间做等幅振荡，电流围绕零值附近做等幅的正弦振荡，振荡角频率为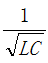，对应波形示意如图8所示，现实情况中阻尼不可能为0，不存在这种现象。

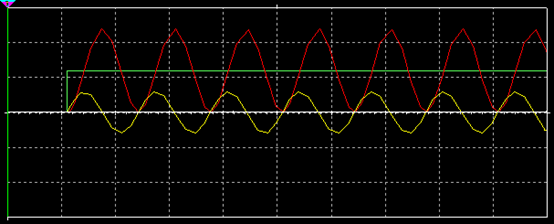
图8

2. RLC振荡通俗解释

上述的阻尼结论是通过数学公式推导得出，波形是通过Multisim仿真得到，但是数学公式并不能让人对波形图有直观的了解，下面将从电荷和电路角度对波形图进行通俗易懂的解释。

我们知道电容电压是连续不能突变的，电容公式I=Cdu/dt，变换可得du=Idt/C，根据数学中的导数知识可得，连续函数在极值点的导数等于0，因此 **电容电压值最大时** ，即电压导数du=0时，Idt/C=0，可得 **电容电流I=0** ；同理，电感电流是连续不能突变的，电感公式U=Ldi/dt， **电感电流最大的时候，电感电压UL=0** 。

2.1 零输入响应

从无阻尼零输入响应的波形图9开始分析，初始条件电容电压为U0，电感电流为0，由于电阻R=0，由图1电路，根据基尔霍夫电压定律可知，无论何时， **电感电压UL=电容电压UC** 。在0时刻，由于电容电压为U0，两侧极板的电荷不平衡，极性为上正下负，所以电容开始放电，电路中的电流开始增加，流向为顺时针方向，如图10所示。直到t1时，电容放电完毕，电压UC=0，因此电感电压UL=0。根据上述电感特性，此时电路电流I最大，电容两侧极板电荷处于平衡状态。 **t1时刻虽然电容处于电荷平衡状态，但是由于电感电流不能突变，不能瞬间从最大值变为0，只能慢慢降低，这就导致电容的电荷平衡状态被打破，电容重新被充电，极性与t0时刻相反** **，为上负下正，直至t2时电感电流I=0，根据上述电容特性，此刻电容电压达到最大值** 。 **t2时刻虽然电感电流I=0，但是此时电容两侧极板的电荷又处于不平衡状态了，电容又要开始放电，只是方向与0~t1时间段内相反，为逆时针方向，** 后续分析与前述思路相同，不再赘述，整个过程种电容电压和电流相位正好相差90°。

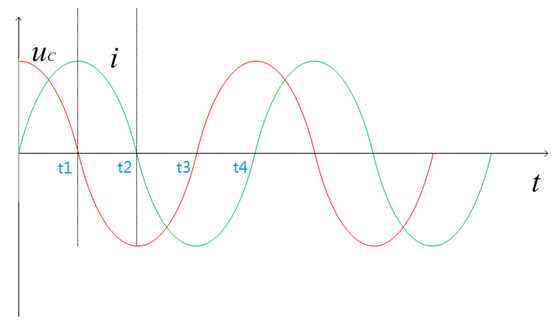
图9

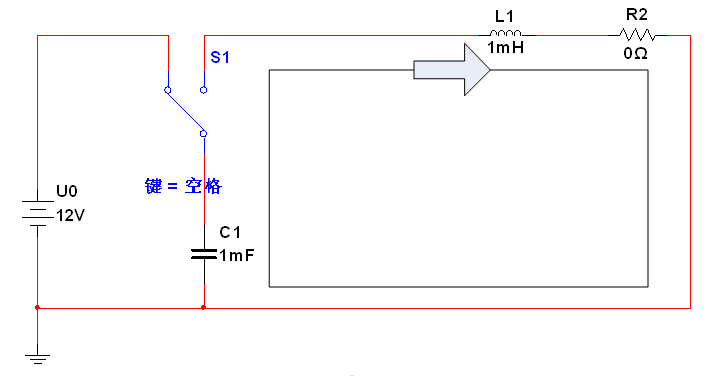
图10

当电路中的阻尼电阻R≠0时，波形如图11所示，由于电阻R存在压降UR，电感电压UL就不等于电容电压UC了，而是如下关系：UC=UL+UR。在0时刻，电容放电，电容电压UC下降，电流I增加，电阻电压UR增加，直到t1时刻，电容电压UC和电阻电压UR相等，即UC=UR=IR时，此时电感电压UL就等于0，电流I达到最大值，I=UC/R，其小于无阻尼状态下的电流最大值。t1时刻电容尚未放电完毕，因此在t1~t2时间段内，电容继续放电直到t2时刻放电结束。而电感电流在t1时刻达到最大值后开始下降，但电流方向不变，到t2时，电容电压放电完毕，电感电流开始给电容充电，电容极性变为上负下正，直到t3时刻，电感电流I=0，电容电压UC达到最大值。从分析中可知， **由于电阻R的存在，电感电流在电容尚未放电完毕时就已经达到最大值，电阻R越大，电流最大值I=Uc/R就越小，电流达到最大值的时刻也越早** ，当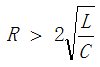时，电流与电容电压分别都在同一时刻达到0不再振荡，形成非振荡放电。

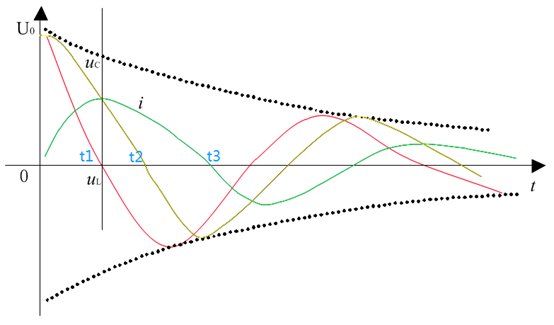
图11

2.2 零状态响应

零状态响应同样从无阻尼的波形图12开始分析，初始条件电容电压UC和电感电流I均为0，激励电压为U0，由于电阻R=0，由基尔霍夫电压定律得，无论何时，U0=UC+UL。在0时刻，电容开始充电，电容UC和电流I开始增加，直到t1时刻，电容电压UC上升到U0，此时电感电压UL=0，电感电流I达到最大值。t1时刻后，电流I开始下降，但方向不变，电容继续充电，直到t2时刻，电流下降到0，电容电压UC达到最大值2U0。t2时刻后，电容开始放电，电流方向改变为相反方向，电流开始反向增大，直到t3时刻，电容电压UC下降到U0，此时UL=0，电感电流达到反向最大值。后续分析类似，不再赘述。

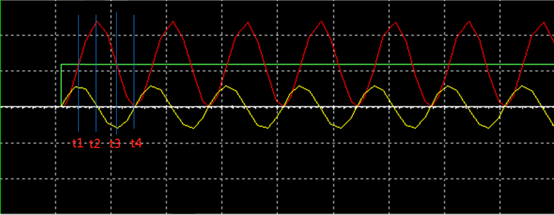
图12

当电路中的阻尼电阻R≠0时，由于电阻存在压降，故U0=UR+UC+UL，波形如图13所示。在0时刻，电容开始充电，电容电压UC和电流I开始增加，直到t1时刻，U0=UR+UC，UL=0，电流达到最大值I=（U0-UC）/R，小于无阻尼状态下的电流最大值，此后电感电流开始下降。此时UCU0，电容电压还未下降到U0。从分析中可知，电阻R越大，电流最大值I=（U0-UC）/R就越小，电流达到最大值的时刻也越早，电容电压所能达到的最大值也越小，当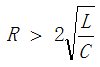时，电容电压在电流为0时达到的最大值接近等于U0，由于电容电压和激励源U0没有压差，无法再充放电，最终形成非振荡充电。

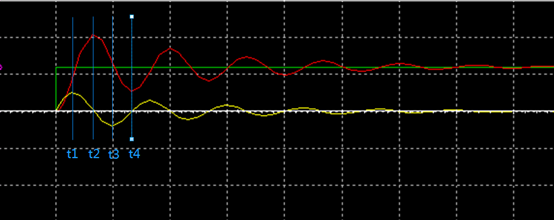
图13

总结

从前述分析中可知，RLC电路能够振荡的初始条件是电容或电感处于不稳定状态，即电容有充电或者放电的条件，流过电感的电流不为0，最终稳态必然是电容不具备充放电的条件，同时电感电流为0。而振荡的初始条件在实际的电源电路中经常遇到，这也是随处可见振荡的原因，下一篇文章将结合实际电路中的振荡现象进行讲解，并给出如何设计RC吸收电路的参考做法。