RC Snubber吸收电路原理详解

在之前一篇文章中我们花了很大篇幅讲述了串联RLC的零输入响应和零状态响应的振荡原理，这是因为电源相关的实际电路中存在的振荡（或者说是振铃）很多都是这个原因。比如前文中描述的BUCK电源电感在DCM模式下工作时，当主开关管关断，续流二极管工作时，电感电流为0时，开关节点处的电压会存在一段时间的衰减振荡；BUCK电源开关节点在主开关管导通，二极管（或同步开关管）关断时的电压尖峰振铃；还有反激开关电源漏感导致的开关节点电压尖峰振荡等等。上述这几种情形的本质机理都是RLC的欠阻尼振荡。

实际电路设计中需要对RC参数进行合理选取，才能达到理想的效果。当然如果规格书中有推荐值的话是最好的，可以先按照规格书确定参数，然后根据实际效果再进行微调。但是我们有必要了解参数大小对实际效果的影响，才能使调试不至于盲目进行。

以常见的BUCK电源开关节点处如图1中红圈所示，在主开关管SW导通，续流二极管D（或者MOS管）关闭时会出现类似如图2所示的尖峰振荡波形。由于实际电路存在寄生电感（比如走线或者器件封装等原因导致），当SW开关管导通时，等效电路如图3所示，L1为寄生电感，C1为续流二极管的结电容或者下侧MOS管的漏源极寄生电容，R1为走线电阻，值很小。R2和C2为RC Snubber吸收电路，虚线框内的是BUCK电路本身的滤波电感电容和负载。由于滤波电感L2取值较大，并且开关频率很高，开关管开通时间很短，所以可以近似认为流经L2大电感的电流不变。因此，在没有RC吸收时的电路就可以等效为串联RLC零状态响应，由于电源走线一般都比较粗短，走线电阻较小，就对电容形成了欠阻尼衰减振荡充电。

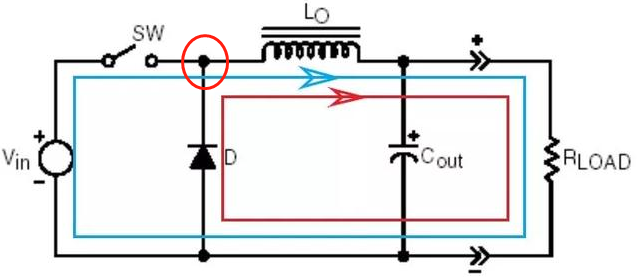
图1

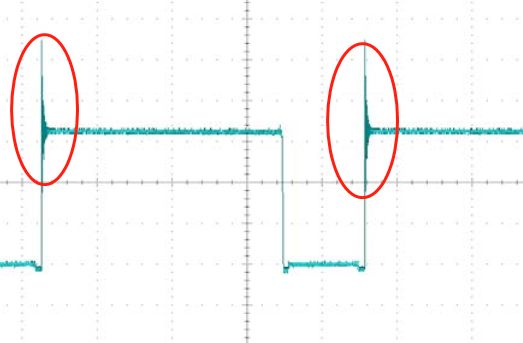
图2

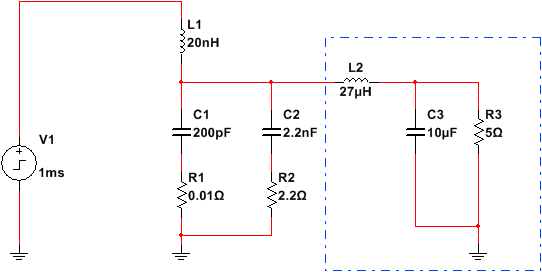
图3

在并联RC吸收电路后，我们可以近似如下分析，来获悉RC参数大小对振铃抑制效果的影响：

确定电阻R2。首先，实际电源电路的走线都比较粗短，所以电阻R1较小，我们暂时先忽略不计；然后，先考虑只并联电阻R2，这样就形成了如图4所示的RLC并联电路（大电感L2的滤波电路形式也是这样，包括开关电源的最后一级基本都可以等效为此电路），这是控制系统中典型的二阶阻尼系统，其品质因素

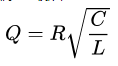
（串联RLC的品质因素Q为其倒数，等于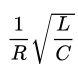），要想振铃峰值越小，Q值应该也越小，则R2值应该较小。但R2不能太小，假设R2趋向于0，则RC吸收就只有电容C2了，就变成了C1和C2并联，形成LC串联振荡了。因此，R2有一个相对值，TI参考文档给出的意见是，可以先理论假设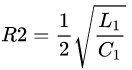，然后再根据实际效果进行微调。

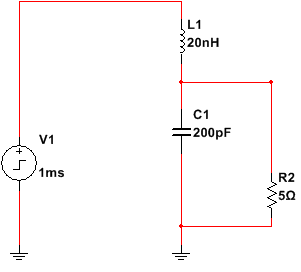
图4

确定电容C2。定好R2之后，暂时将其忽略不计，只考虑C2，C2和C1并联最终还是RLC串联电路，根据其品质因素

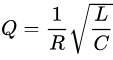
可知，理论上电容C2越大，Q值越小，振荡的抑制效果越好，从另一个角度也很容易理解，电容越大，电压越不容易发生突变。但是当C2值增大到一定程度之后，对应的容抗值已经很小，其值相对R2来说已经不大，所以影响甚微。另一方面，C2越大，电源的效率会越低，因为电容C2的充放电过程会在电阻R2上形成功率损耗。

知道了吸收电路参数对振荡抑制效果的影响后，就可以设定一个初值，然后根据实际效果进行调整，直到满意为止。

TI的文档有提供一个方法可以参考，现分享步骤如下：