简单了解下可靠性加速实验的理论依据

1

阿伦尼斯计算模型

物理加速模型是基于对产品失效过程的物理化学解释而提出的。一种典型的物理加速模型是阿伦尼斯（Arrhenius）模型，阿伦尼斯模型适用于单纯考虑热效应试验的加速模型，当温度是影响产品老化及使用寿命的绝对因素时，采用该加速模型来模拟整个寿命周期的可靠性表现。

加速因子公式表达：

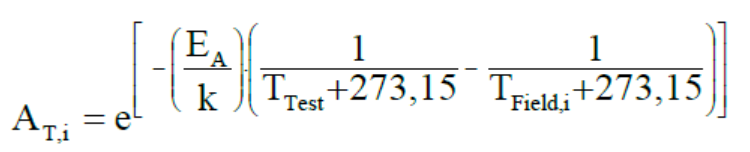
其中公式中各个参数代表的含义解释如下：

AT,i：加速因子，在所有的加速模型中都是表达一个含义，也就相当于加速系数，计算出他就能将整个寿命周期时间转换成加速试验的时间；就是我们要算出来的每个温度点下的加速因子，比如i为1，则根据谱图第一行来算出该条件下的加速因子，具体的含义就是比如说AT,1算出来为5000,则意味着如果想代替在-40°C 下工作的占6%比例的这段寿命时间，则等价的试验就是在T pruf下工作8212.5/5000个小时。e: 就是一个常数,2.71828,在excel里面这里对应的就是exp函数。

Ea:是析出故障的耗费能量，又称激活能。不同产品的激活能是不一样的。一般来说，激活能的值在0.3ev~1.2ev之间;此数值也是由主机厂提供，这里给出的是0.45eV。

K：是玻尔兹曼常数，其值为8.617385×10-5 ev/K;

Ttest：测试条件下(加速状态下)的温度值。此处的温度值是绝对温度值，以K(开尔文)作单位；就是指你想在什么温度条件下进行该加速试验，通常情况为了达到最快的加速且不会损坏产品，我们会选择温度谱图中的最高温度，即80°C。

Tfield:是使用条件下(非加速状态下)的温度值。此处的温度值是绝对温度值，以K(开尔文)作单位

很多人不知道活化能Ea应该选取那个值？其实不同的Ea对应了不同的失效机理，下面表格是一些电子元器件在经验累积得到推荐值。

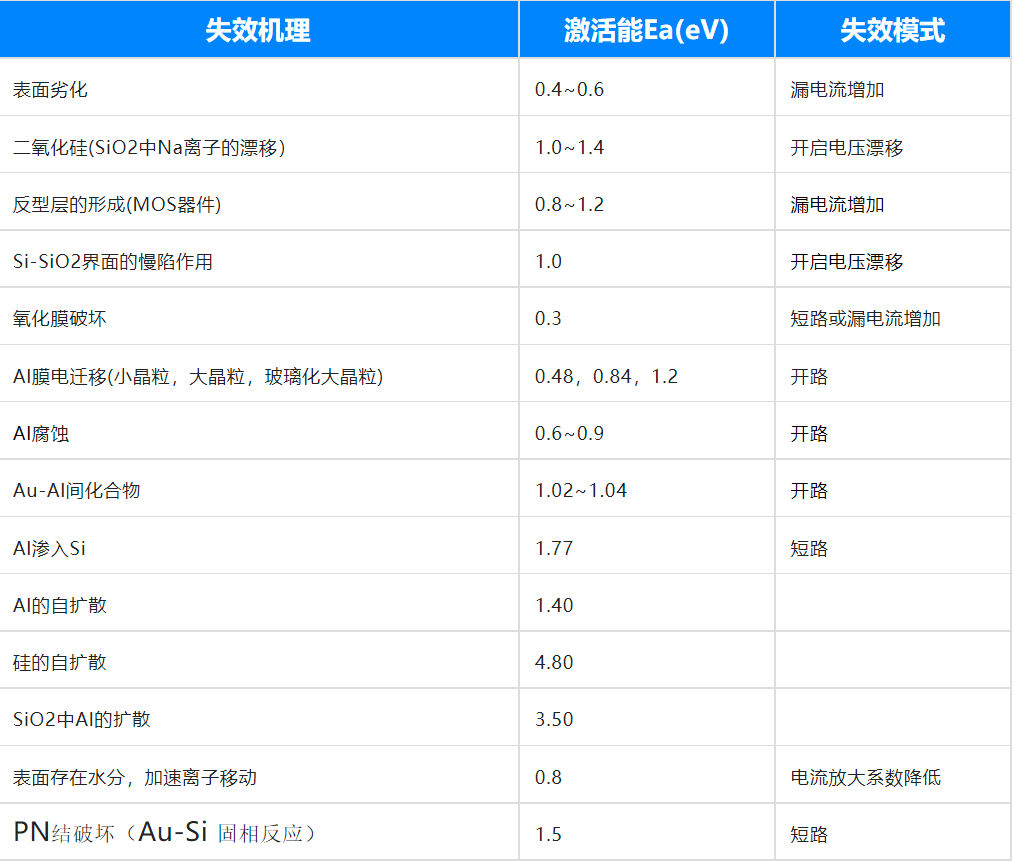
但是我们在做产品温度加速时，一般是针对整系统，那么Ea应该如何选取。通常情况下，根据经验Ea可选取0.5~0.7eV.比如戴尔电脑对PC的Ea选取0.6eV,这个值也是多次试验的出来的平均值。这个Ea选取主要针对但应力加速时，如果有2个应力以上，则无需考虑，可以通过试验结果计算出来。

阿伦尼斯模型有下述特点：

(1) 该模型反映的是产品某特性量与激活能和所施加应力的关系；

(2) 阿伦尼斯模型使用的寿命与温度的表达形式及加速因子都是基于退化量相同导出的。这就为加速寿命试验提供了另外一条途径，即利用某性能参数或特征量退化数据对产品的可靠性进行评定、推断。

(3)从公式中可以看出，激活能越大，加速系数也越大，越容易被加速失效，加速试验效果越明显；

(4)在激活能确定的情况下，温度差越大，加速系数也越大；

【实操计算】:

案例：某一客户需要对产品做105℃的高温测试。据以往的测试经验，此种产品的激活能Ea取0.68最佳。对产品的使用寿命要求是10年，现可供测试的样品有5个。若同时对5个样品进行测试，需测试多长时间才能满足客户要求？

解：

AF=EXP(Ea/k*(1/Tnormal-1/Tfeild))=exp(0.68/K*(1/((25+273)-1/(105+273)))=262

T测=Life/AF=10*365*24/262=333.73h

2

科芬曼森模型

科芬-曼森模型是适用于温度冲击试验的加速模型，反映了温度交变应力作用下的疲劳破坏。该方法成功地模拟了在温度交变应力作用下焊点的裂纹扩展过程。

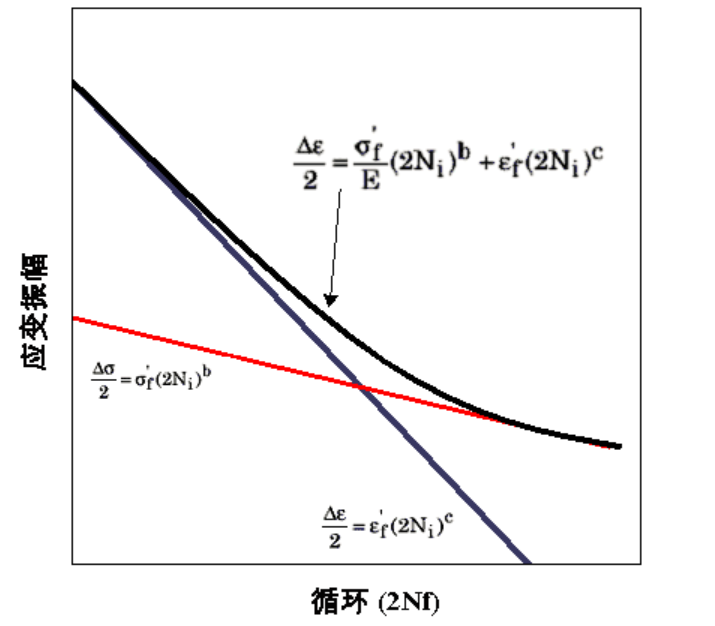
公式表达  ：

ΔTtest：测试循环的高低温之间的差值；

Acm：该模型的加速因子；

ΔTfild：温度谱中平均温度差异，一般产品终端会给出明确值；一般由主机厂给出，这里是40°C.

C：科芬-曼森指数，它指的是温度变化的加速率常数，不同的失效类型对应不同的值；一般由主机厂指定，它指的是温度变化的加速率常数，不同的失效类型对应不同的值.据我所知，大众和奔驰对该值都指定为2.5。

公式二：

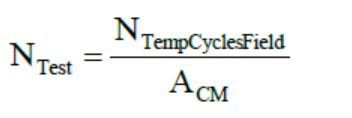
Ntf：实际使用大概的循环数；

Ntest：需要测试的循环数；

知道循环数，最高温度(T max) 及最低温度(T min)后，接下来就是该公式应用起来最困难的部分，即怎么确定温度变化速率以及在每个温度点上的停留时间，有些情况下主机厂会直接指定相关参数，比如下表就是一家主机厂给出的数据，要求我们根据样品的质量来决定在每个温度点的停留时间。

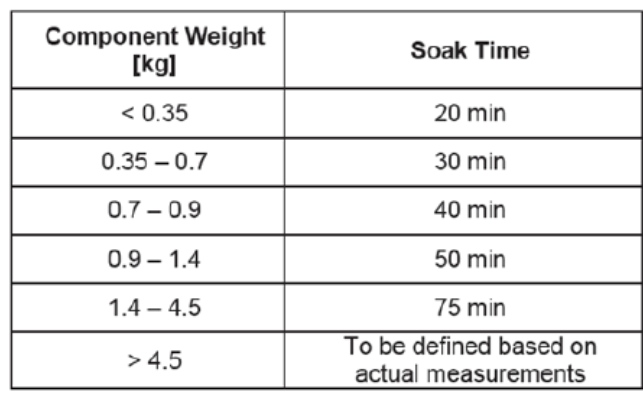
最后，在确定温度变化速率t speed)以及在每个温度点上的停留时间(t holding time)后，就可以根据下面公式算出每个循环所需要的时间，再乘以上面算出的总循环数，就能确定该温度循环试验所需耗费的总时间了。

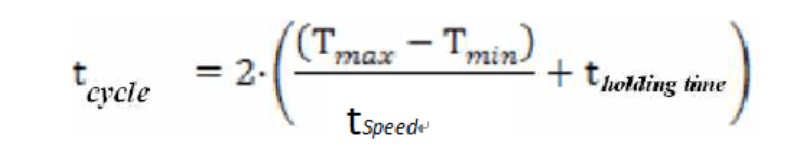
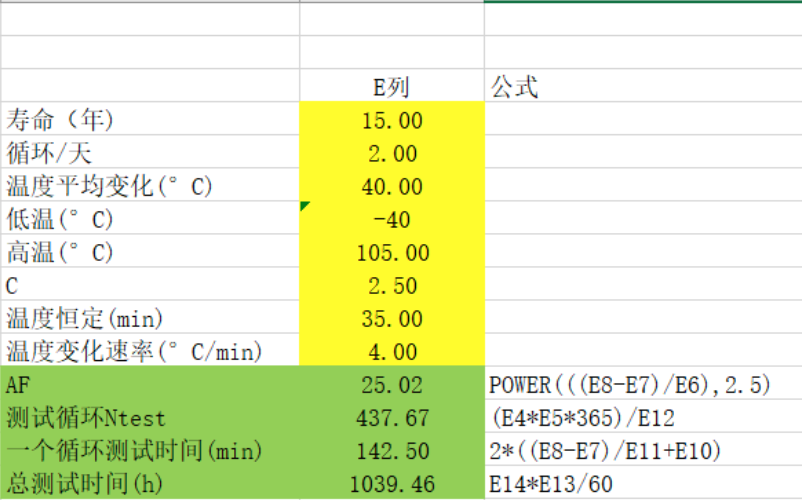
【实操计算】

假设一种产品在实际使用过程中，每天会经过两个温度交变的循环，预计使用寿命是15年，失效因数是2.5，温度变化范围是-40°C，高温是105°C，平均温度变化是40°C，根据经验，高低温到达的恒定的时间是35min，试计算如果采用循环加速寿命需要多少循环，多长时间？

Excel表格计算公式如下：

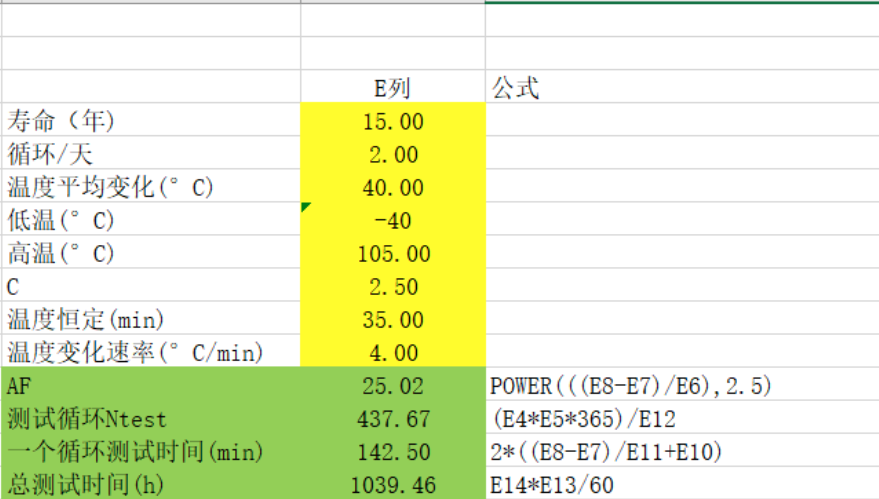
3

劳森模型Lawson

在阿伦纽斯模型的基础上引入湿度应力的影响，就是劳森模型。

公式如下：

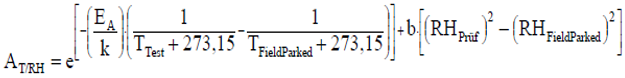
AT/RH：加速因子

b：常数(b = 5.57 x 10^-4)

EA:活化能 (EA = 0,4 eV)

K：是玻尔兹曼常数，其值为8.617385×10-5 ev/K;

Ttest：测试条件下(加速状态下)的温度值。此处的温度值是绝对温度值，以K(开尔文)作单位；

Tfield:是使用条件下(非加速状态下)的温度值。此处的温度值是绝对温度值，以K(开尔文)作单位

RHTest：测试期间的相对湿度,比如这里我们选择93%RH。

RHFieldParked：实验箱内的平均相对湿度(%)，由主机厂给出；

因此根据上面的参数，可以算出要想加速到65°C，93%RH则对应的加速因子AT/RH为105.04。接下来再使用该公式来计算对应的试验时间t pruf:

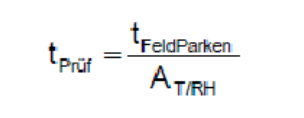
tFeldParken:就是指在主机厂要求的寿命期间内汽车不运行的时间，这里以极限的15年来考虑，即按照15年该车都不运行的状态来考虑此时间，15*365*24=131400h。

因此再结合上面算出的加速因子可以得知要想在65°C，93%RH的条件下来加速该试验，则对应的试验时间约为1251小时。

4

随机振动试验加速因子 

振动试验是指评定产品在预期的使用环境中抗振能力而对受振动的实物或模型进行的试验。根据施加的振动载荷的类型把振动试验分为正弦振动试验和随机振动试验两种。

是模拟产品在运输、安装及使用环境下所遭遇到的各种振动环境影响，用来确定产品是否能承受各种环境振动的能力。振动试验是评定元器件、零部件及整机在预期的运输及使用环境中的抵抗能力。

在标准GB/T 21563-2008 轨道交通 机车车辆设备 冲击和振动试验中给出了试验时间和寿命时间与试验加速度和实际应力加速度的对应关系。

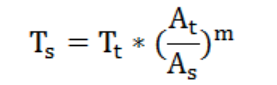
Ts：运行寿命/时间；Tt：试验时间；As：运行加速度；At：试验加速度；M：金属材料选择4。

可以得到如下公式：

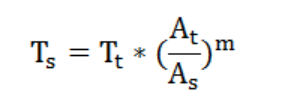
对于振动加速度，如果不加说明，一般指振动的峰值，即g。对随机信号，一般是取一段时间计算均方根的加速度，即g(RMS)，rms是均方根值（有效值）的意思。

例如某产品进行随机振动试验，加速度均方根值为0.7 grms，振动时间是10 h；如果实际产品24 h处理工作状态，所面临的振动加速度是0.08 grms；可以计算出该产品耐振动的运行时间是Ts=10 h*（0.7/0.08）4=58 618 h≈6.5年。

5

艾琳模型-电压应力加速因子

产品除了环境应力的作用外，电应力的作用也不可忽视。电应力也会促使器件内部产生离子迁移、质量迁移等，造成短路、绝缘击穿短路失效等。

器件在电压、电流或功率等电应力作用下，应力越强、失效速率越快，器件寿命越短。Eyring模型是Arrhenius模型的扩展，用于温度和电压同时加速的试验项目。

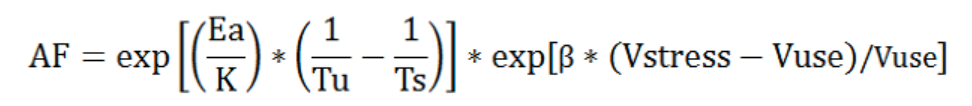
β：电压加速常数（0.5≤β≤1.0，根据不同失效机理，默认值为1.0）；Vstress：试验时应力电压（Stress voltage）；Vuse：正常使用电压（Operating voltage）

从艾琳模型模型中的电应力加速因子计算模型可知，只有正向的电压才有加速应力，即试验电压要高于额定电压。例如：某电子产品额定输入电压为220 Vac，试验时输入电压为250 Vac。计算出AF(v)=1.12。

6

结束语

加速寿命试验技术具有效率高，成本低，对高可靠、长寿命产品的定寿延寿研究具有重要的应用价值。目前加速寿命试验技术在汽车领域应用都较为广泛，并取得了一定研究成果。如汽车仪表、LED等都形成了各自的寿命评估标准。随着研究的不断深入，加速寿命试验技术在各个领域将有广阔应用前景。

审核编辑：刘清