基于OFDR重构框架分布式形状传感误差模型研究

 01   导读

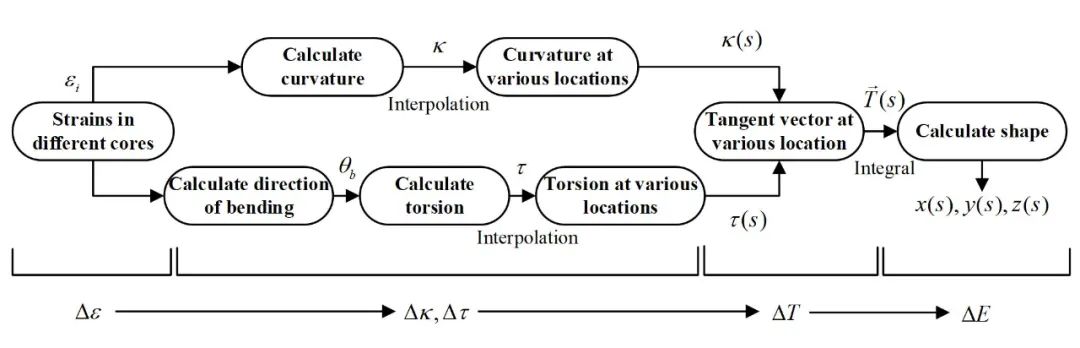
目前光纤形状传感重构误差通常表示为欧几里得距离。然而，形状重构的欧几里得距离误差取决于待重构形状的复杂度，而形状复杂度取决于长度、曲率和挠率。

天津大学丁振扬副教授团队基于Frenet-Serret框架和误差传递理论，建立了光频域反射（OFDR）中分布式形状传感的重构误差模型，阐明了重构误差与曲率、挠率、光纤长度和应变测量误差等参数之间的关系。

通过基于OFDR的分布式光纤形状传感系统实验验证了所提出的重构误差模型的可行性和适用性。

当需要重构形状的曲率、挠率、光纤长度的估计范围以及OFDR系统的应变测量误差已知时，所提出的重构误差模型可预测最大重构误差，进而判断形状重构误差是否满足要求实际应用的需求。

封面图 形状重构误差传递模型 图源：Optics Express 

02  研究背景

近年来，光纤形状传感已成为光纤传感领域的一个热门研究方向。与其他形状重构技术相比，光纤形状传感具有一系列优点，如结构紧凑、灵活性高、耐恶劣环境和腐蚀，并且能够实现分布式传感。光纤形状传感在医疗器械、机器人、航空航天等领域具有巨大的应用潜力。 目前光纤形状传感重构误差通常表示为欧几里得距离。

光纤形状传感重构误差模型研究相对有限。尽管已有研究者对光纤形状传感精度进行了研究，但只给出单一数值，而形状传感精度与形状参数（如曲率、挠率、长度和应变测量误差）是直接相关的，单一精度值并不能反映其在任意形状下情况。而目前欧几里得距离误差与形状参数之间的模型尚未进行研究。

如果建立了重构误差模型，则可以基于应变测量误差和形状参数来估计任意形状的重构误差，这对于根据形状轨迹确定形状重构误差是否符合实际应用要求非常有用。  

03   创新研究

3.1 形状重构误差模型

分布式应变测量是形状测量的基础和前提。显然，更好的空间分辨率和更高的应变测量精度将导致更精确的形状重构。事实上，光纤形状传感中OFDR的感测空间分辨率通常基于OFDR系统的信噪比（SNR）设置为最小值，并且在这种情况下，空间分辨率对重构误差的影响可以忽略不计。

因此，建立形状重构误差与应变测量误差之间的三维形状传感误差模型具有重要意义。 本文中使用微分几何形状重构算法是基于广泛使用的Frenet-Serret框架，通过求解Frenet公式中切向量、法向量和副法向量来获得曲线的空间坐标。基于Franet-Serret框架的形状重构算法的误差传播过程如下：应变测量误差Δε导致曲率误差Δκ和挠率误差Δτ，这进一步导致切线向量ΔT的计算偏差。

ΔT在形状长度s积分过程中不断累积，最终导致欧几里得距离重构误差ΔE。   通过构建曲率误差、挠率误差与应变误差关系，得到了任意空间曲线下距离重构误差ΔE模型：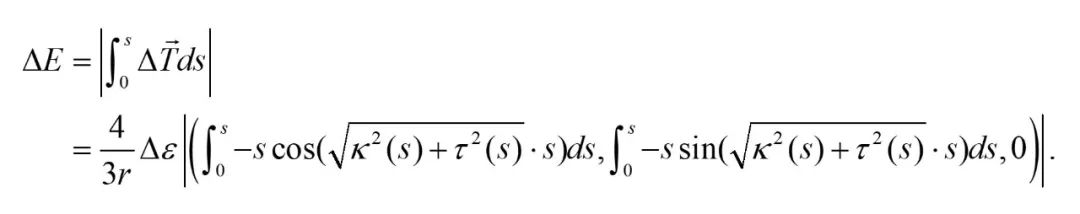

 

3.2 已定应变误差下的重构误差模型验证

为了验证重构误差模型的有效性，我们进行了基于OFDR的多芯光纤形状传感实验。我们把实验分成两部分。在第一部分，我们通过变量控制方法验证了重构误差与模型参数之间的关系。在第二部分，我们通过校准OFDR系统的最大应变误差来验证该模型对随机应变误差的相同适用性。

为了消除空间分辨率对实验的影响，基于OFDR系统的SNR，将所有实验的空间分辨率设置为最小3.6mm。如何选择合理的形状来验证模型是一个关键点。形状的复杂性无法定量定义。任何复杂的形状都可以看作是由具有常数曲率κ和挠率τ的弧微段组成。

如果我们已经验证了该模型对于具有恒定曲率和挠率的形状是正确的，则该模型对于任何复杂形状都是正确的。原因是复杂的形状是许多简单形状的一个整体过程。为了将曲线的κ和τ控制在一个恒定值，我们结合3D打印技术设计并打印了一系列包含凹槽的模型，其中已知κ和τ曲线作为实验中多芯光纤的形状载体。

此外，我们选择较短的光纤进行实验，以使曲线的κ和τ的波动尽可能小。

首先验证了挠率误差与重构误差关系，设计并制作了曲率为0.1m，挠率为0 rad/m, 2 rad/m, 4 rad/m, 6 rad/m, 8 rad/m 和 10 rad/m的 3D打印模型如图2所示。

实验中多芯光纤缠绕在3D打印模型的凹槽里，形状重构中加入5 με已定应变误差，相关实验结果如图3（a）所示。

根据模型计算的重构误差ΔE和实际测量的ΔE如图3（b）所示。理论预测重构误差与实验结果相符。重构误差随着挠率增加而减小。

挠率较小时，重构误差基本不随挠率变化。当挠率较大时，重构误差受挠率影响较大。

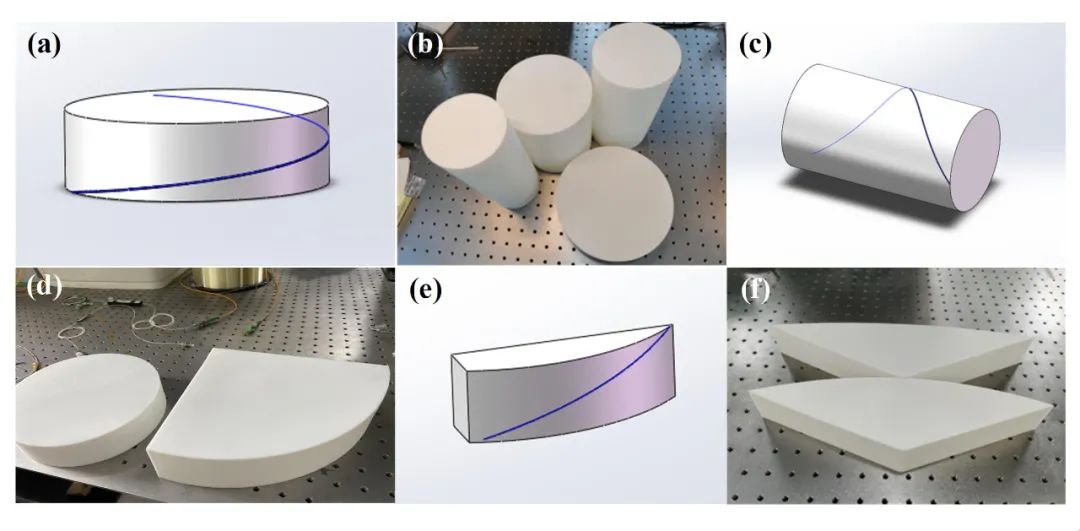
图2 3D打印空间曲线模型   图源：Optics Express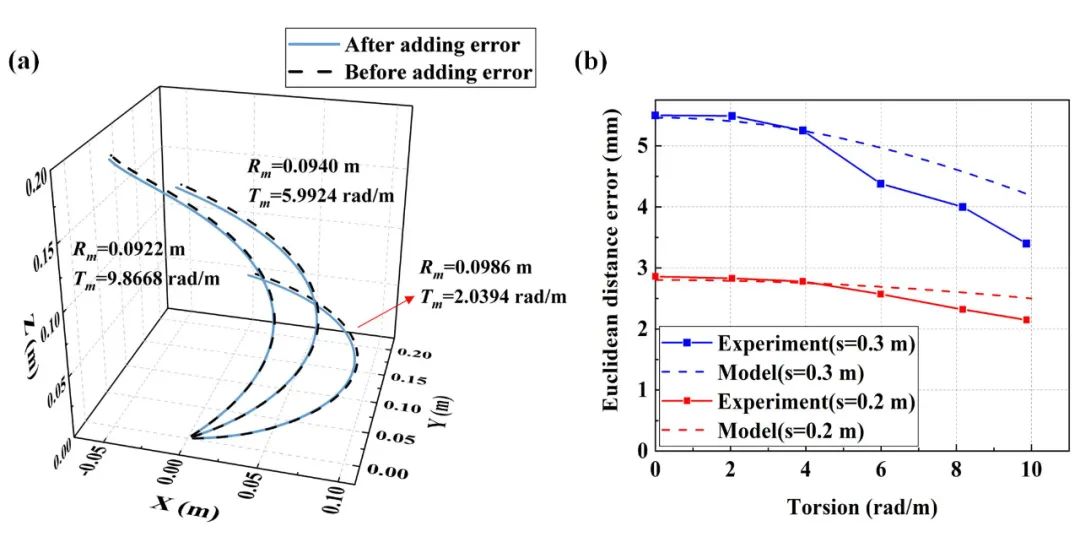 



图3 挠率验证结果（a）重构曲线（b）理论和实验重构误差对比

其次，验证了曲率误差与重构误差关系。根据误差模型和图3（b）显示关系，挠率为0时，重构误差最大。这里采用二维曲线对重构误差与曲率关系验证，采用曲率半径为0.05m，0.1m，0.2m, 0.35m, 0.5m和1m的3D打印模型如图2所示。形状重构中加入5με已定应变误差。

二维曲线重构结果如图4（a）所示。同时根据误差模型计算了形状长度为0.2m和0.3m下不同曲率半径下的重构误差并与测量值进行比较如图4（b）所示。理论预测重构误差与实验结果相符。从图4（b）可以看出，但曲率半径较小时，重构误差随曲率半径增大迅速增加。当曲率半径较大时，重构误差随曲率半径增大趋于稳定。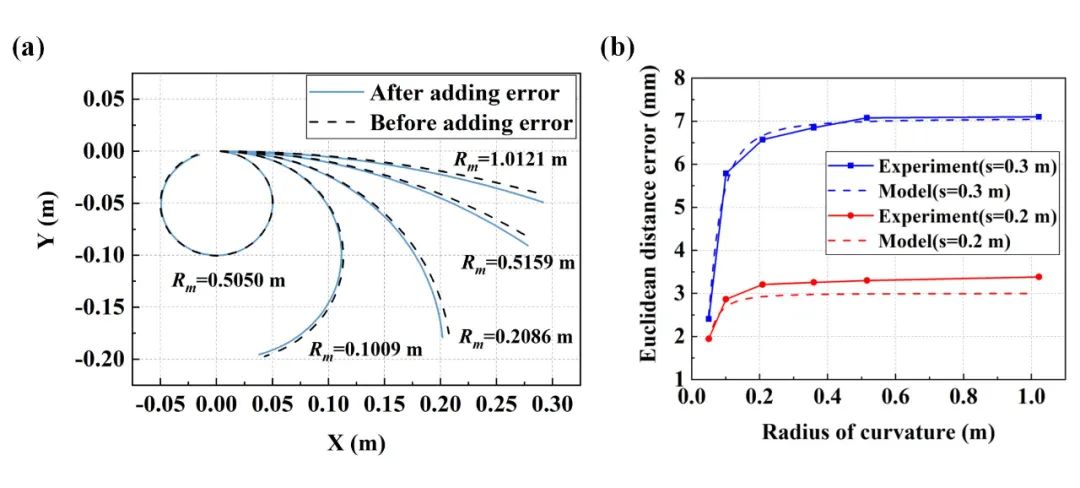



图4 曲率验证结果（a）重构曲线（b）理论和实验重构误差对比

再次，验证了光纤长度与重构误差关系。为了验证这一关系，我们重构了一个螺旋线形状，其长度为0.55m，曲率半径为0.052m，挠率为3.8rad/m。形状重构中加入5 με已定应变误差。

螺旋线重构结果如图5（a）所示。不同光纤长度下的重构误差并与测量值进行比较如图5（b）所示。理论预测重构误差与实验结果呈现高度一致性。重构误差与光纤长度呈现非线性增加，其原因是光纤重构过程中误差累积的结果。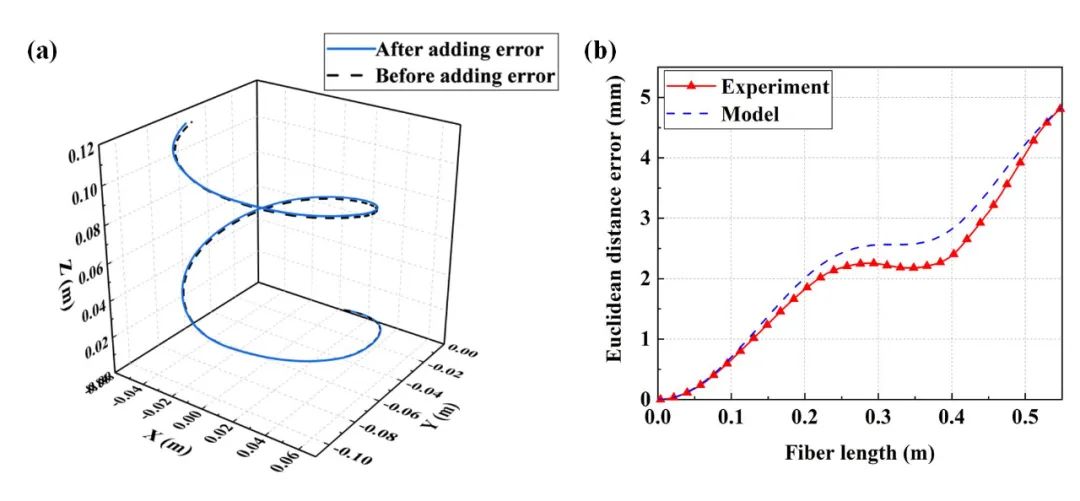



图5 光纤长度与重构误差验证结果（a）重构曲线（b）理论和实验重构误差对比

最后，验证重构误差与应变测量误差关系。采用0.3 m长曲率半径为1m的弧形作为验证模型。沿光纤长度上分别加入已定应变误差f1 με, 2 με, 3 με, 4 με和 5 με。

不同应变误差下的测量和理论的重构误差如图6所示。理论预测重构误差与实验结果呈现高度一致性。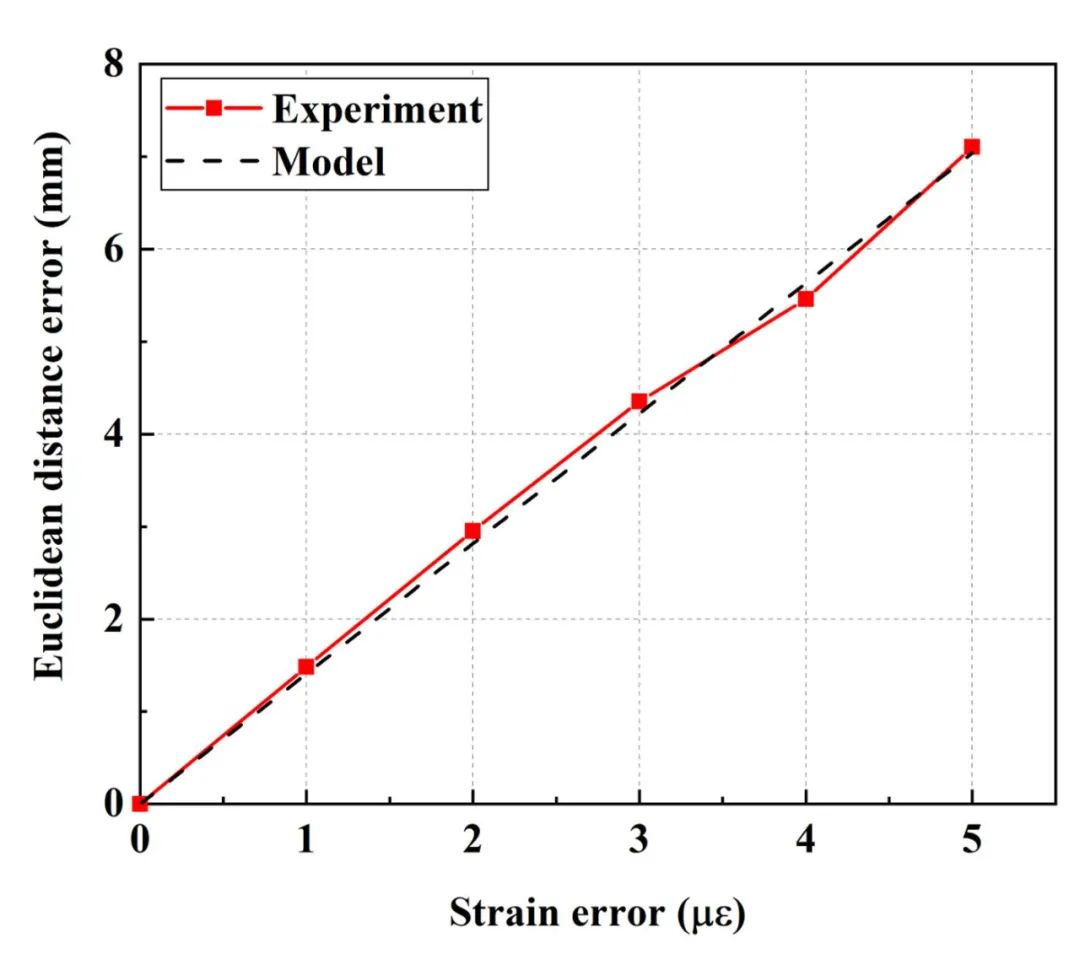



图6 不同应变误差下重构误差验证结果 图源：Optics Express

3.3 随机应变误差下的重构误差模型验证

之前已经证明了已定应变误差下误差模型的可行性，但在实际应用中，OFDR沿光纤应变误差是随机的，而在OFDR应变传感系统中会给出最大应变误差Δεmax。本节中，我们将通过校准实验中OFDR系统的Δεmax，进一步验证重构误差模型对随机应变测量误差的适用性。

如何构建不同Δεmax是实验关键，我们这里采用设置不同应变测量分辨率通过与纳米位移台应变标定值比对，得到不同的Δεmax。应变校准范围为0至25με，每5με进行一次校准。每个应变取80个应变测量点，并计算Δεmax。我们进行了形状重构实验，以验证在不同Δεmax下重构误差模型的适用性，其中测试形状为曲率半径为1m的二维圆弧。

在Δεmax分别为6.19με、6.22με、8.41με和10.04με的条件下进行形状重构，并通过将重构曲线与标准曲线进行比较来计算测量重构误差。显示了测量重构和光纤长度之间的关系，并与基于重构误差模型的理论值进行了比较，如图7所示。

应该注意的是，图7中观察到的理论值和实测值之间的差异相对较大。然而，多次实验的测量值没有超过重构误差模型计算的理论最大值。

由于OFDR系统的应变测量精度可以预先评估，因此根据Δεmax利用误差模型得到重构误差可以指导我们在光纤形状传感的设计中选择合适的OFDR系统应变测量精度，并预测形状重构精度。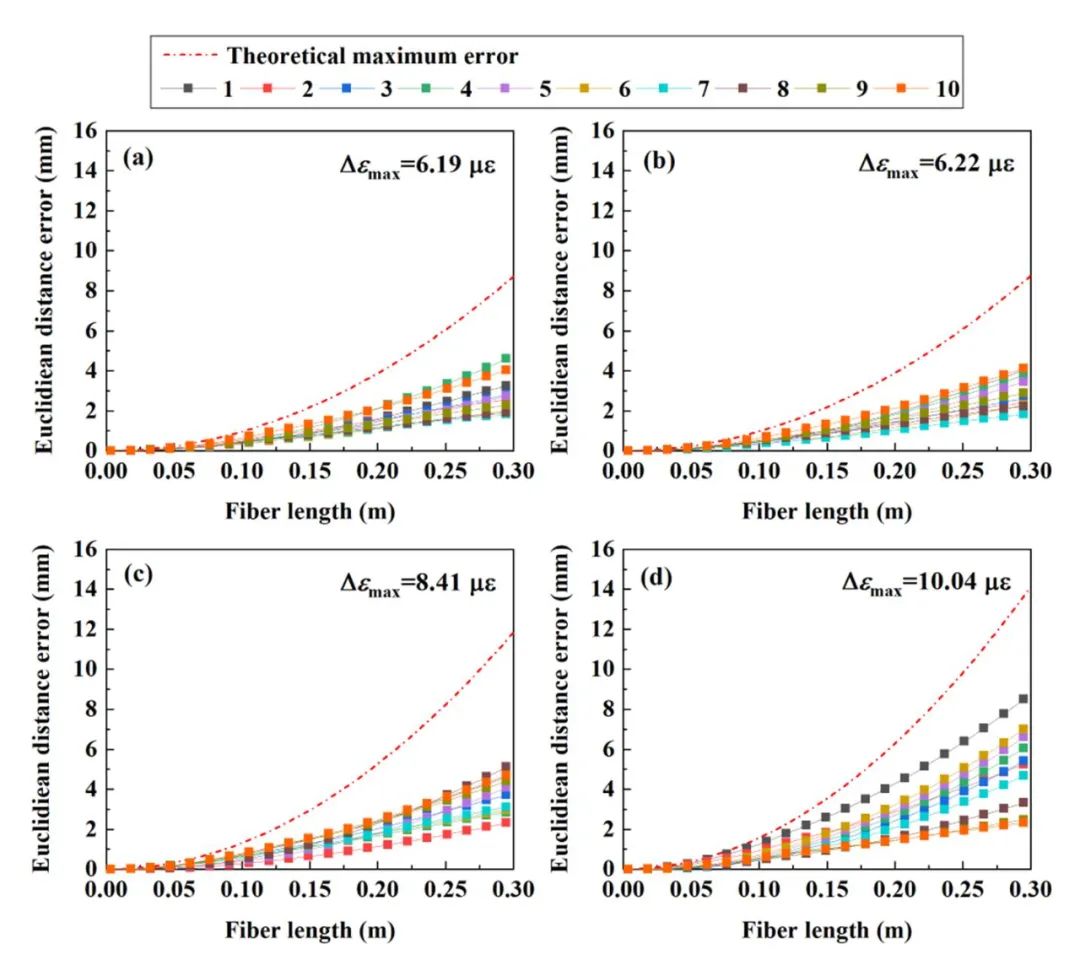



图7 不同最大应变误差下重构误差验证结果。(a) Δεmax=6.19 με. (b) Δεmax=6.22 με. (c) Δεmax=8.41 με. (d) Δεmax=10.04 με.   

04   应用与展望

三维形状传感误差模型的建立不仅让我们更清楚地了解了影响形状重构结果的因素，还为光纤形状传感系统在不同应用场景下的设计和性能评估提供了理论指导。

当形状测量精度要求以及待重构形状的曲率和挠率范围已明确时，所提出的重构误差模型可用于计算满足要求的最小应变测量误差。

因此，该误差模型可以有效地指导设计者为形状传感器的选择合适的应变测量系统。

   





审核编辑：刘清