一种有效将3D点云分割成平面组件的多分辨率方法

摘要

本文提出了一种有效的多分辨率方法将 3D 点云分割成平面组件。为了提高效率，本文从粗到精的 3D 分辨率中迭代处理大点云，在每个分辨率下，快速提取表面法线来描述表面元素（面元），将无法与来自较粗分辨率的平面关联的面元分组为具有霍夫变换的共面簇。然后提取这些集群上的连接组件，并通过 RANSAC 确定最佳平面拟合。最后，合并平面片段并在最佳分辨率上细化分割。在实验中，展示了该方法的效率和质量，并将其与其他最先进的方法进行了比较。

简介

我们将 Hough 变换与 RANSAC 相结合以稳健地提取来自 3D 点云的平面片段（图 1）。为了提高效率，我们采用由粗到细的策略：以多种分辨率提取局部表面法线来描述表面元素（面元）。我们使用八叉树实现了一种高效的多分辨率法线方法估计。在每个分辨率下，我们确定哪些面元可以用较粗分辨率上拟合的平面来解释。在剩余的面元上，我们应用霍夫变换将场景预分割为共面面元。为了提高准确性和鲁棒性，我们使用 RANSAC 拟合平面段。在最佳分辨率下，我们合并共面连接的平面段并分配剩余的点。

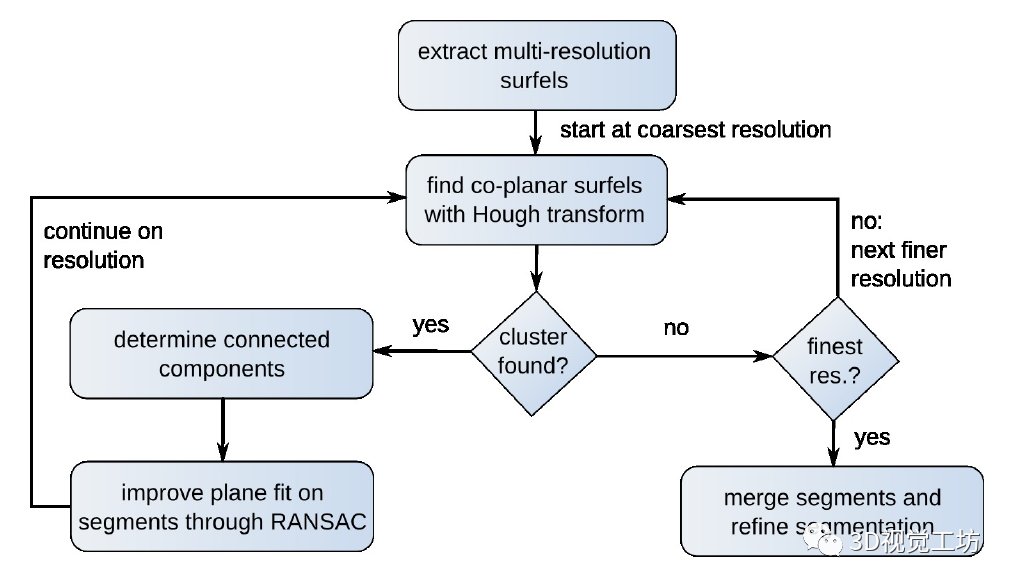
图1

1、通过多种分辨率进行有效的法线估计

我们用八叉树表示点云。八叉树由分支节点和叶节点组成，每个分支节点和叶节点都覆盖一个 3D 体积。树的根跨越感兴趣的完整 3D 体积。每个分支节点在其中心位置将其体积分成八个大小相等的立方体（称为八分圆）。对于它的每个八分圆，该节点都包含一个子节点，该子节点本身是一个分支节点，或者是树中的一片叶子。 八叉树可以用于以与树的不同深度中节点的体积大小相对应的采样分辨率采样点云。对于采样深度 d，我们确定采样深度的所有节点或较粗分辨率的所有叶节点。此外，八叉树允许有效地计算节点体积中的积分值：在每个节点中，我们维护位于节点体积内的点值的积分。在树的构建过程中，我们将一个点的值分配给该点访问的所有节点，同时将它从根递归传递到它的最终叶节点。 

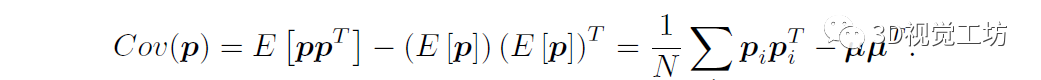
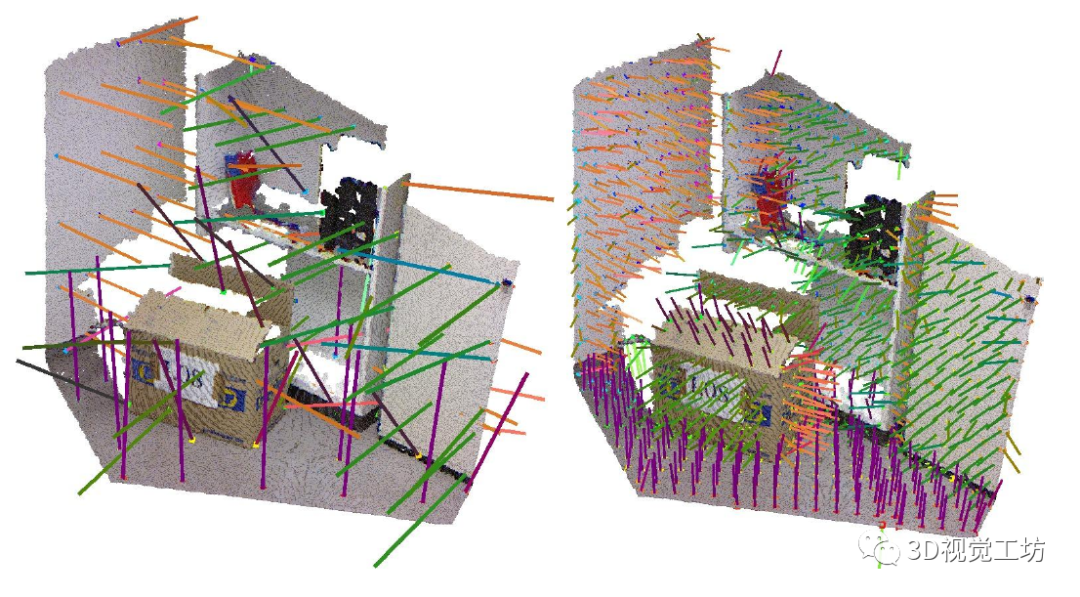
图2

在第二阶段，我们从平行面元簇中确定共面面元。每个面元投票决定平面到坐标系原点（例如，视点）的距离。与方向直方图类似，我们将选票分配到具有线性衰减的相邻箱中。

我们在距离直方图的最大值处再次找到共面面元簇。图 3 显示了示例场景中此预分割步骤的结果。为了使这个过程高效，我们保持直方图的粗分辨率，并将模型参数的准确估计推迟到后期处理阶段。然而，距离直方图的分辨率随着面元的分辨率而增加。

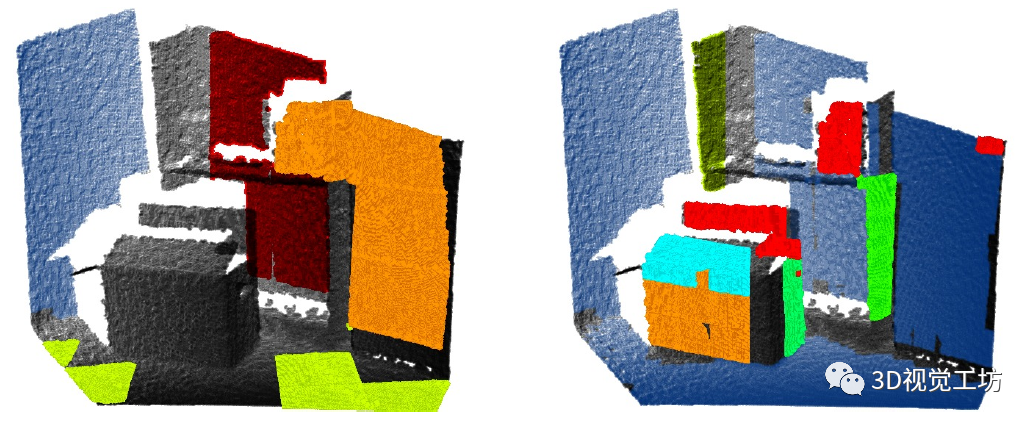
图3

3、分割成连通域

霍夫变换不考虑面元的空间连通性。因此，我们从共面元组中提取连通分量。图 4 举例说明了这一点。我们在对应于面元的霍夫空间最大值的平面上覆盖一个网格。网格的分辨率是根据面元的分辨率来选择的。我们将每个面元位置投射到网格中并标记占用的网格单元。区域增长产生连接的组件，当组件不受最小数量的面元（在我们的实现中设置为 3）支持时，我们将丢弃这些组件。

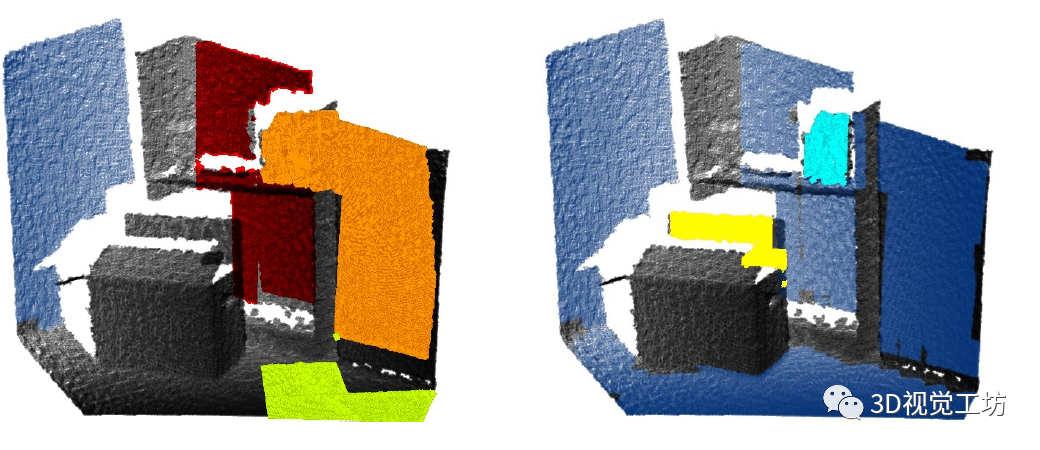
图4

4、通过 RANSAC 进行精确分割

我们进一步改进了与共面面元的连接组件的平面拟合。由于方向和距离直方图的粗分辨率，霍夫变换的平面估计只是对真实底层平面的粗略估计。因此，我们将 RANSAC 直接应用于面元表示的点。图 5 显示了异常值检测的示例。

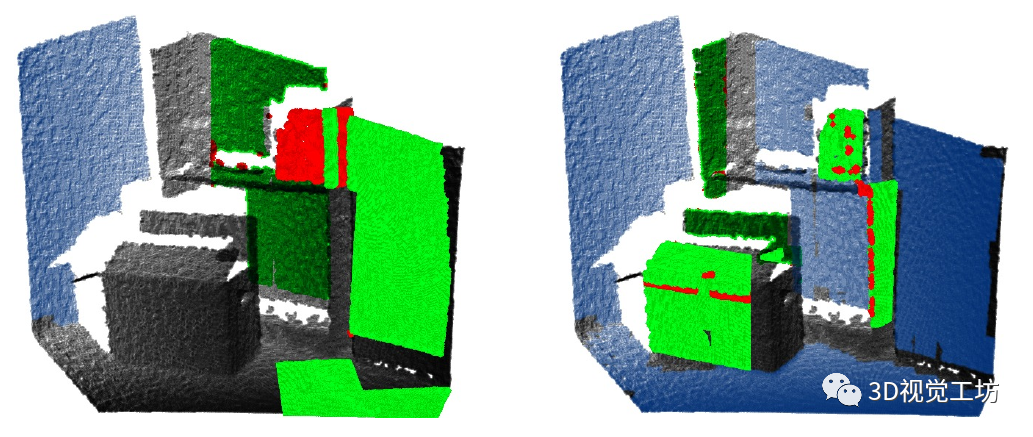
 图5 RANSAC 从一组随机的三点样本中估计平面参数。在固定的迭代次数内，我们确定面元的所有点支持的最好的平面估计。当点到平面的距离低于某个阈值时，点被接受为平面拟合的内点。我们根据面元的分辨率调整此阈值。我们只接受大部分面元点支持的平面拟合。我们还要求提取的平面与霍夫变换确定的初始拟合相似。当平面拟合被接受时，我们重新确定线段的连通分量。

5、由粗到细的分割

在前面的部分中，我们详细介绍了如何在单一分辨率上分割平面。然而，我们建议使用由粗到细的策略来分割场景。通过这种方式，可以仅从几个面元中有效地检测到大平面段。此外，我们的方法固有地适应场景中平面的范围。它使用尽可能多的上下文来决定共面性。 我们从粗分辨率到精细分辨率处理场景。当在分辨率上找不到更多的平面段时，我们过渡到下一个更精细的分辨率。为了改进已经找到的平面片段的分割，我们将更精细分辨率的面元重新分配到片段上。我们测试面元方向和位置是否适合每个平面段，以及它是否位于其连接组件的边界内或边界处。 最终，我们还调整了连接的组件。为此，我们根据新的分辨率增加了占用图的采样率。我们将面元投影到平面段中并标记相应的单元格被占用。但是，我们保留了前几层的较粗略的占用决策。请注意，虽然平面段可能会在此过程中扩展，但不会合并一起增长的段。我们在最后的处理步骤中合并共面连接的段。

6、后处理

在处理完所有分辨率后，我们改进了最精细分辨率的分割。首先，我们合并连接的共面平面段。然后我们在不使用法线信息的情况下将节点分布到平面段上。对于每个节点，我们确定一个平面段候选列表，这些候选平面段与节点体积内的点的均值距离很小。此外，节点需要落在连接的组件内或每个候选节点的边界。

当平面段的重心位于该平面的不同侧时，我们相应地将点分布在等距平面的两侧。否则，我们只是将这些点关联到最近的平面。

实验结果

30 幅 ABW 测试图像的分辨率为 512× 512 像素。该数据集还结合评估工具提供了地面实况分割。表 1 显示了我们的方法在 SegComp ABW 测试图像上的结果，对于与地面实况的重叠具有 80% 的容忍度。

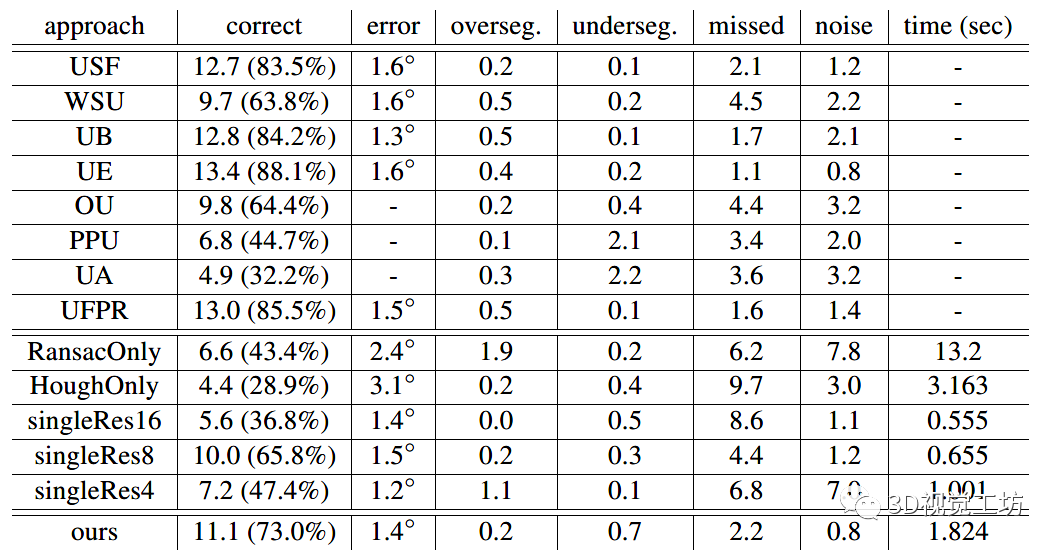
表1

虽然我们的方法不是专门为深度图像设计的，但其分割质量和平面拟合精度位于该数据集结果的上限范围内。请注意，最好的分割结果是通过利用图像结构中编码的连接信息的方法获得的。这也将这些方法限制在处理单视图深度图像。此外，距离图像包含深度离散化效应形式的强系统噪声，这对于仅由少数点组成的小片段很难处理。

为了评估我们算法各个阶段的贡献，我们对几个变体进行了测试。RansacOnly 方法使用贪心法来检测平面（使用点云库 PCL 实现）。它在不使用法线信息的情况下迭代地找到适合尚未归因的点的最佳支持平面。它只能达到平均性能，其运行时间在很大程度上取决于场景的复杂性。HoughOnly 基于我们的多分辨率方法，但不执行 RANSAC 来改进初始 Hough 分割。且与我们的方法相比，HoughOnly 方法分割场景的准确性较低。 图 6展示了我们的方法在不同重叠公差 SegComp ABW 测试图像上的结果。

可以看出，我们的方法中的错误在很大程度上是由于缺少平面段造成的。对于高噪声，某些点可能未分配给平面或边界可能无法正确解析。由于我们的方法不考虑图像邻域，因此很难达到 90% 的重叠。图 5展示了 ABW 数据集的两个示例性分割。在左图中，我们的算法遗漏了多个平面片段。我们将一些未命中归因于八叉树的离散化。这个问题可以通过在不同的离散化中重新处理未分段的部分来解决。

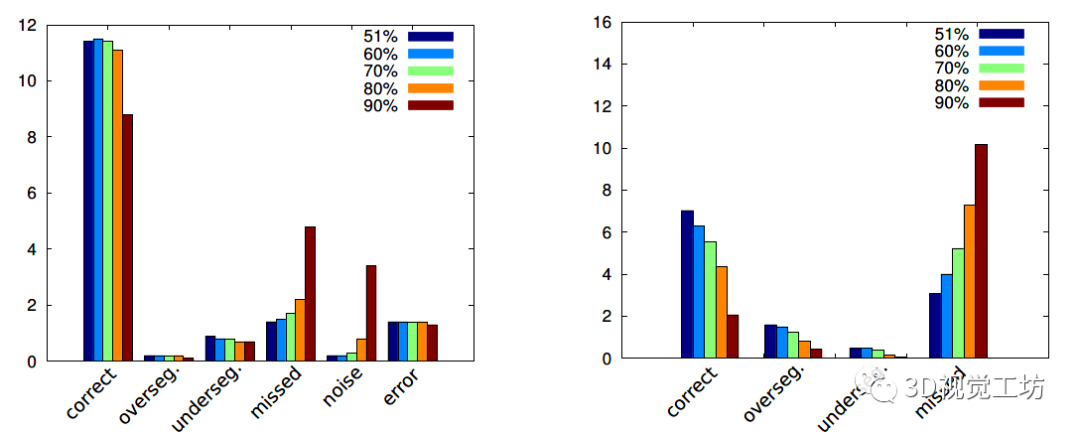
图6

总结与展望

本文，我们提出了一种从 3D 点云中提取平面的有效方法。我们将 Hough 变换与RANSAC 相结合，以在多种分辨率下拟合平面。通过使用由粗到精的策略，我们可以有效地利用可用数据。它允许考虑最大可能的上下文来做出共面性的决定。这也使我们的方法数据高效。

在实验中，将改方法与使用 SegComp 数据库的最先进方法进行了比较。实验结果表明，我们以高帧率和高质量处理 3D 激光和深度传感器（例如 Kinect）的 3D 点云。 在未来的工作中，我们将提取更多类型的几何形状图元，例如圆柱体和球体。我们还计划调整我们的方法来顺序处理来自 Kinect 等高帧率传感器的深度图像。

审核编辑：刘清