浅析KUKA数学标准功能

ABS(X)

总和

REAL_MIN…REAL_MAX 0 … REAL_MAX

SQRT(X)

平方根

0 … REAL_MAX 0 … REAL_MAX

SIN(X)

正弦

REAL_MIN…REAL_MAX -1 … +1

COS(X)

余弦

REAL_MIN…REAL_MAX -1 … +1

TAN(X)

正切

REAL_MIN…REAL_MAX REAL_MIN…REAL_MAX

ACOS(X)

反余弦

-1 … +1 0 … +180

ATAN2(Y,X)

反正切

REAL_MIN…REAL_MAX -180 … +180

绝对值 ABS(X) 计算 X 的总和。

示例：

B = -3.4

A = 5*ABS(B)                  ;A=17.0

平方根 SQRT(X) 计算 X 的平方根。

示例：

A = SQRT(16.0801)             ;A=4.01

正弦 SIN(X) 计算角度 X 的正弦。

示例：

余弦 COS(X) 计算角度 X 的余弦。

示例：

A = SIN(30)                   ;A=0,5

B = 2*COS(45)                 ;B=1.41421356

正切 TAN(X) 计算角度 X 的正切。

示例：

以下总和的正切无穷：

C = TAN(45)                   ;C=1.0

 ±90°

 +90° + k*180°  （其中 k = ± 整数）

如果尝试一个这样的值，这将导致错误信息。

反余弦 ACOS(X) 是 COS(X) 的反函数。

示例：

A = COS(60)                   ;A=0.5

B = ACOS(A)                   ;B=60

反正弦 对于 SIN(X) 的反函数反余弦，没有预定义函数。但是，基于公式 SIN(X) = 

COS(90°-X) 可以很容易就计算出反正弦。

示例：

A = SIN(60)                    ;A=0.8660254

B = 90-ACOS(A)                 ;B=60

反正切 

角度正切的定义是直角三角形的邻边 (X) 除以对边 (Y)。如果两个侧边的长度已知，则可以用反正切计算邻边和斜边之间的角度。

对于全圆，起决定性作用的是 X 和 Y 的正负号是什么。如果只考虑商，则用反正切只能计算 0° 和 180° 之间的角度。通常，这在袖珍计算器时也是如此：正值的反正切得出一个 0° 和 90° 之间的角度。负值的反正切得出一个 90° 和 180° 之间的角度。

通过用正负号指定 Y 和 X 明确地确定了位于该角度中的四分之一圆。由此也可以计算四分之一圆 III 和 IV 中的角度。

示例： A = ATAN2(0.5,0.5)              ;A=+45 B = ATAN2(0.5,-0.5)             ;B=+135 C = ATAN2(-0.5,-0.5)            ;C=-135 D = ATAN2(-0.5,0.5)             ;D=-45

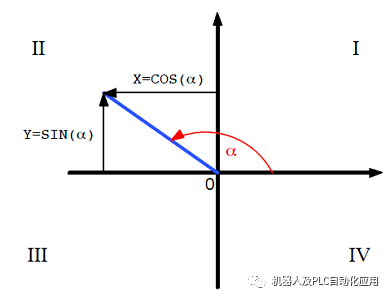
在函数 ATAN(Y,X) 中使用 X 和 Y

审核编辑：刘清