固定增益运算放大器简化滤波器设计

在设计Sallen-Key滤波器时，使用更少的元件数量、资金和电路板空间。使用固定增益放大器简化带通滤波器。

简单的二阶滤波器可满足许多滤波要求。例如，低阶低通滤波器通常足以实现ADC应用中的抗混叠或消除音频应用中的高频噪声。同样，低阶高通滤波器可以轻松消除电源噪声。设计具有内置增益的此类滤波器时，固定增益运算放大器可以节省空间、成本和时间。图1显示了固定增益运算放大器在构建二阶低通和高通Sallen-Key滤波器中的应用。过滤器“说明书”在设计这些滤波器时很有用，但是如果增益由R设置，则说明书过程通常会针对给定的响应（例如巴特沃思）进行分解F和 RG大于团结。更重要的是，说明书中的元件值公式可能会产生不切实际的电容器和电阻值。

图1.Sallen-Key滤波器使用固定增益运算放大器来实现二阶巴特沃兹响应。

例如，巴特沃兹滤波器提供最平坦的通带。它们还提供快速的初始衰减和合理的过冲。您可以使用下表和以下公式轻松设计此类过滤器：R2= 1/（2πfC√） 和 R1= XR2.

为了获得滤波器响应，使用固定增益运算放大器可降低成本和元件数量。它还会降低灵敏度，因为内部工厂调整的精密增益设置电阻可提供0.1%的增益精度。要使用固定增益运算放大器设计二阶巴特沃兹低通或高通滤波器，请执行以下步骤：

确定转角频率fC.

为 C 选择一个值。

对于所需的增益值，请在表中正确的列标题下找到 X。

计算 R1和 R2使用方程式。

选择 C 然后求解 R1和 R2允许您通过选择尽可能接近计算值的分量值来优化滤波器响应。对于大多数转角频率和增益，C 可以低于 1000pF。固定增益运算放大器针对每个增益版本进行了最佳补偿，并为工作在高频和高增益下的系统提供出色的增益带宽产品。例如，假设您必须设计一个转折频率为24kHz、增益为10的低通滤波器。步骤 1 已完成 （fC= 24kHz）。接下来，通过选择 C 的值（例如 470pF）来完成步骤 2。在表中，请注意，对于增益为10的低通滤波器，X = 0.076。在等式中替换这些值：

R2= 1/（2π fC√） = 1/（2π × 24kHz × 470pF × √ ） = 51kΩ，R1= XR2= 0.076 × 51kΩ = 3.9kΩ。

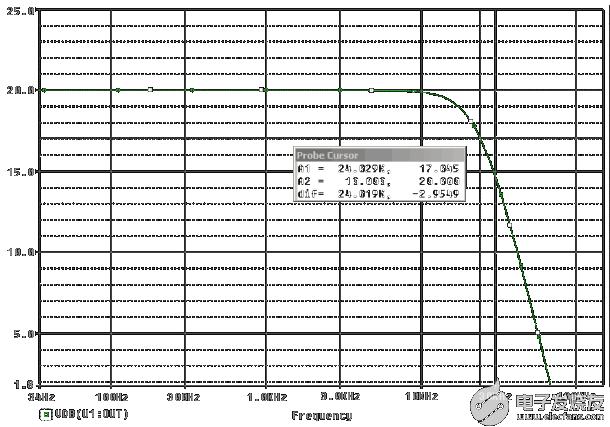
图2.使用文本中的电路值，对图1a中的电路进行仿真会产生这种巴特沃兹响应。

审核编辑：郭婷