

使用全通滤波器设计正交网络
描述
正交网络将单个输入信号转换为两个相位差为 90 度的输出。本文介绍如何使用全通滤波器设计正交网络。
以有用的方式改变频率响应的滤波器是众所周知的。然而,鲜为人知的是全通滤波器,它不会改变频率响应(我认为这实际上应该被称为“幅度响应”),但会改变所施加信号的相位。这些滤波器有许多用途,例如在音乐效果、校正信号传输延迟以及控制信号的波峰因数(峰值与均方根 (RMS) 值的比值)中。
使用简单的全通滤波器,我们可以构建正交网络,从单个输入信号产生两个输出信号,在指定范围内的所有频率上具有几乎固定的相位差。这些也可用于特殊的音乐效果,但也广泛用于高效的调制系统,例如单边带(SSB)甚至独立边带(ISB),其中AM信号可以携带两个信息通道。其他历史应用包括晶体控制载波的频率调制和三相电机的变速运行。
本文将深入探讨如何设计全通滤波器和正交网络。我们还将提供在线设计应用程序,这些应用程序使用的计算方法超出了铅笔甚至Microsoft Excel的实用性。
全通滤波器简史
对全通滤波器的认真研究似乎始于100多年前。早期的参考文献是R.V.L Hartley于1928年为SSB调制发明的专利[1]。R.B Dome在1946年发表的一篇开创性论文中使用了“众所周知”一词[2],不幸的是没有参考书目。早期的研究相当难以理解,因为基础理论涉及考虑椭圆周长而产生的“椭圆函数”。通常,无法精确计算这些函数的值。W J Albertsheim和F R Shirley[3]后来的一项研究突破了这一困难,通过使用函数的某些对称性质来推导出一个代数设计过程,这对于在电子表格中执行的某个网络族来说是非常可行的。
此外,全通滤波器可以使用RLC甚至RC无源网络制成,但需要一个变压器或两个相反极性的输入信号。相比之下,使用运算放大器的滤波器有一个非常简单的单元,即“一阶滤波器”,该单元是级联的,通常只有一个元件值变化,以产生更高阶的滤波器。本文将专门研究二阶和四阶滤波器,尽管可以类似地处理阶数为 2 的幂的扩展滤波器。但是请记住,其他订单的设计可能要困难得多。
虽然电路使用运算放大器,但如果滤波器基于简单的高通滤波器,那么即使是像TL072这样的普通器件也可以在相当高的频率下使用,因此在低频而不是高频下需要高闭环增益。
什么是全通滤波器?
我们可以想象,“全停止”滤波器是开路的,因此“全通”滤波器可能是短路或一小段粗线。但事情并没有那么简单。信号有两个属性,“幅度(伏特或安培)”和相位,它们表示信号波形上某个识别点与某个声明的“零时间”相关的时间。相位仅对正弦信号有意义,但由于任何信号都可以表示为一组正弦信号,因此这不是一个大问题。
然后,全通滤波器的输出电压(或电流)等于输入电压(或电流),但输出相位改变或“移位”。使用运算放大器制作全通滤波器非常容易,如图1所示。
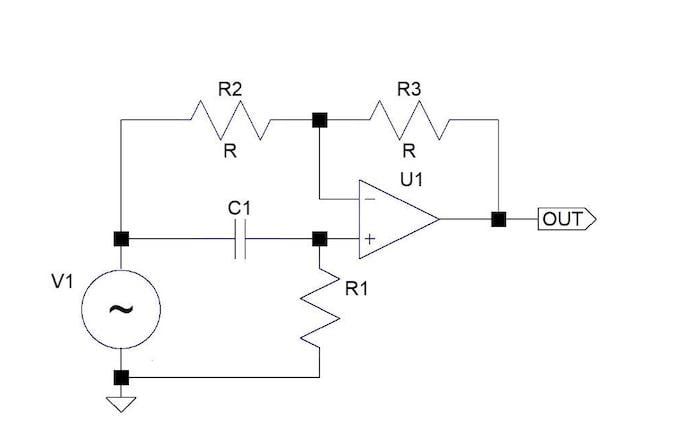
图1.单级全通滤波器电路图示例。
请注意,未显示运算放大器的直流电源。相等电阻R2和R3使所有频率下的输出电压等于输入电压的负1倍;但是,运算放大器+输入端的高通C1 R1网络会改变输出相位。请记住,电容和电阻可以改变以形成低通网络,但这意味着在高频下需要高开环增益,这并不好。
要了解其工作原理,请记住,运算放大器具有高内部增益,因此输出是由两个输入端的微小电压差异产生的。由于输入信号+的相位发生了变化,因此输出信号的相位发生了变化。
该电路的相位响应具有两个非常幸运的特性。当相等电阻R将输入到输出的增益设置为1时,通过滤波器支路的增益在高频时为2。这是滤波器正常工作的基本要求,导致输出相位的变化是CR滤波器的两倍,CR滤波器在很宽的频率范围内从0°到90°变化,因此输出的相位在0°到180°之间变化(见图2)。
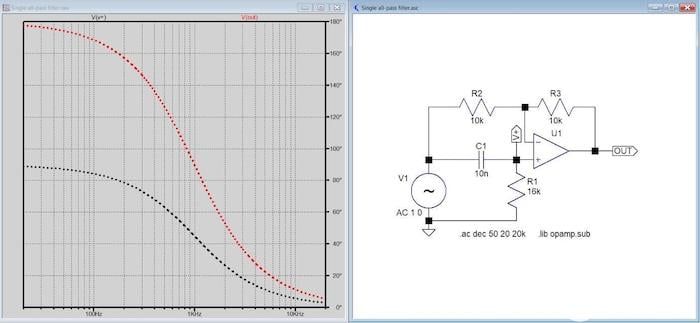
图2. +输入和运算放大器输出端的相移。虚线是相位曲线,如以度为单位的 y 刻度所示。[点击图片放大]。
另一个幸运的特性是,在一定的频率范围内(8:1或更高,取决于可接受的偏差),+输入的相位,因此输出的相位几乎与频率的对数成反比(见图3)。这对于构建正交网络很有价值。
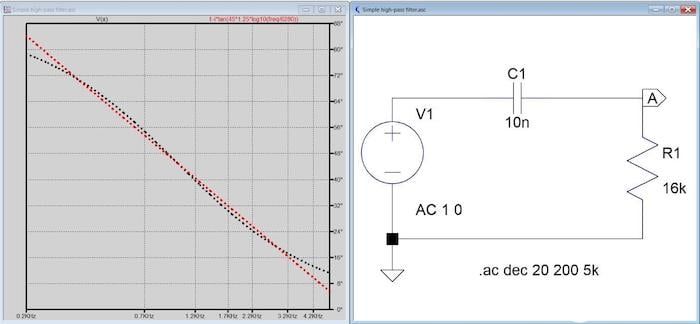
图3. 相位和对数缩放频率之间的线性关系[单击图像放大]。
在上图中,黑线是测量相位,红线是直线近似值,表示紧密拟合。
可以用有源带通滤波器代替无源高通滤波器,但对于本文来说,这是一个相当复杂的电路和一步。
构建二阶正交网络
深入研究,我们可以使用成对的全通滤波器来构建正交网络,该网络从输入信号产生两个信号,一个具有 45° 相移,另一个具有 135° 移位,因此,它们之间产生 90° 相位差。一个信号相对于另一个信号在频率尺度上横向移动。图 4 显示了最简单的“二阶”版本。
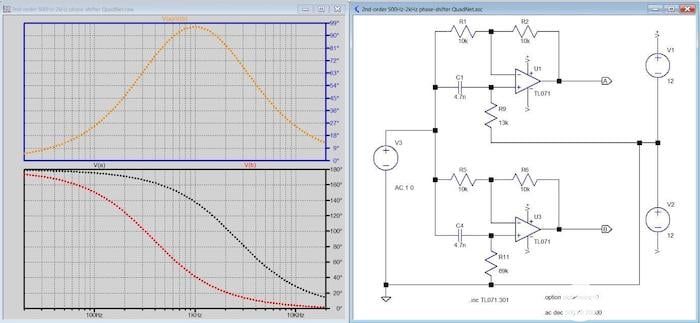
图4. 二阶正交网络 [点击放大]。
必须计算的分量值只有 R9 和 R11。参考文献中给出了一种方法[3];然而,由于深植于高等数学的原因,它不是最好的解决方案,因为相位角仅在90°以下偏离。请记住,对于许多应用,相位差不需要(通常假设的那样)精确到90°;即使是 10° 误差也只会产生很小的影响。通过将输出连接到 X-Y 示波器并观察显示的圆的形状随频率变化的程度,可以轻松验证这一点。显示的解决方案来自我使用的设计应用程序QuadNet,这是Jim Tonne提供的免费产品。
在图表中,黑线是输出 A 相对于输入的相位,红线是输出 B 的相位,黄线是输出 A 和输出 B 之间的相位差。
图5显示了该网络的测量响应,该网络在没有特殊紧公差组件的情况下构建。
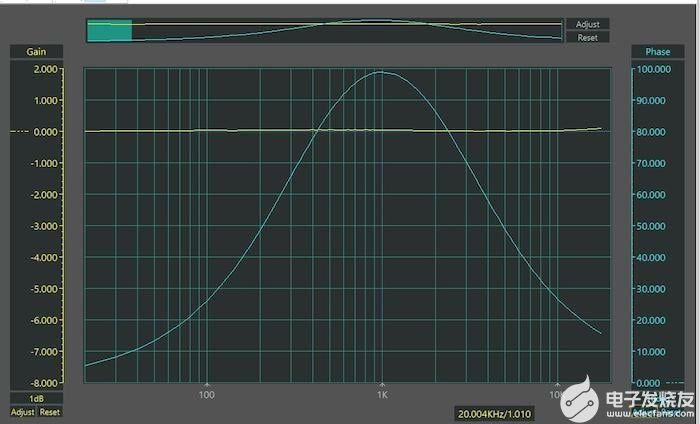
图5.二阶正交网络的测量响应
您可以看到频率响应有多平坦;但是,在大约500 Hz至2 kHz的范围内,相移在90°的±10°以内。为了获得更宽的带宽,我们需要一个更高阶的网络。
构建四阶正交网络
图6显示了我在1997年为特定目的设计的四阶网络,即为听觉环系统制造相控阵磁天线。
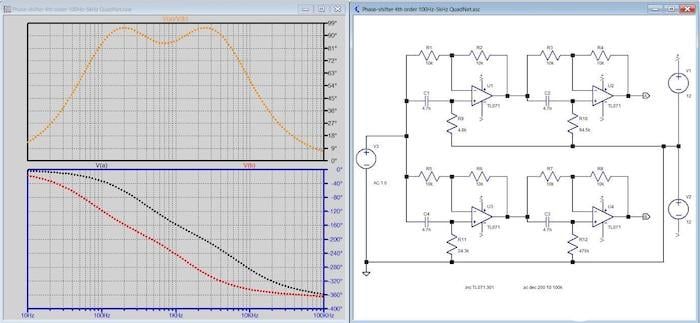
图6. 100 Hz 至 5 kHz 的四阶网络 [点击放大]。
在图表中,黑线是输出 A 相对于输入的相位,红线是输出 B 的相位,黄线是输出 A 和输出 B 之间的相位差。
简而言之,这种工作方式是将音频信号电流(主要是语音)馈入空间地板上的大环线中,从而产生磁场。这被助听器中的磁性天线(“拾音线圈”)拾取,使佩戴者能够清楚地听到。为了覆盖大面积,并防止磁场从所需位置扩散太远,使用环路阵列并以相位正交方式馈送信号,因此需要设计。
当然,在1997年,我没有QuadNet,所以我最初的设计有点偏离最佳,但非常接近,足以在现实生活中广泛使用。
图 7 显示了实际测量网络的结果。现在,在大约90 Hz至6 kHz的范围内,相移在90°的±10°以内,这是对二阶网络的改进。
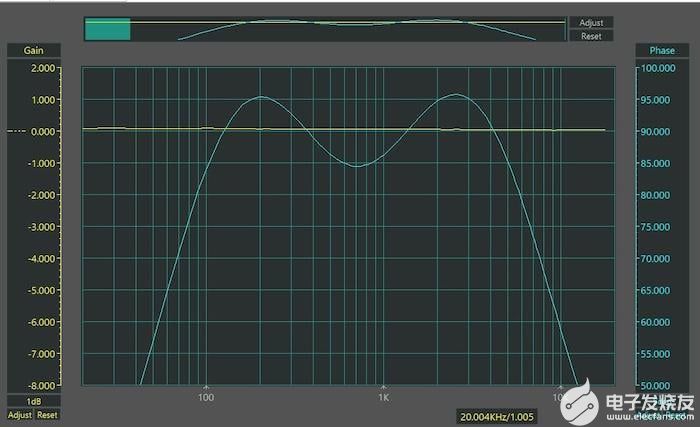
图7.四阶网络的测量响应
在结束这个项目时,我们已经演示了使用简单的全通滤波器来构建正交网络,该网络在指定范围内的所有频率下生成两个(几乎)固定相位差的输出信号。这些可用于许多应用,包括创建音乐效果和无线通信调制系统。
- 相关推荐
- 热点推荐
- 滤波器
-
全通滤波器系统函数稳定吗2024-08-21 2114
-
网络滤波器图2023-08-28 3820
-
网络滤波器的作用2023-06-24 2608
-
全通滤波器定义_全通滤波器的零极点关系2023-02-20 7518
-
全通滤波器原理说明2021-03-22 4694
-
MT-202: 全通滤波器2021-03-21 766
-
正交镜像滤波器的详细资料介绍2020-05-09 2282
-
全通滤波器的特点2019-01-14 13834
-
高阶FIR正交镜像滤波器的设计2011-08-29 813
-
求助关于全相位FIR滤波器和传统方法设计的滤波器2011-05-10 3893
-
二阶全通滤波器电路函数与原理2010-05-23 12368
-
双正交小波滤波器构造及其应用于图像边缘检测2009-08-17 1337
-
全通(相移)滤波器的设计步骤2008-12-01 6583
全部0条评论

快来发表一下你的评论吧 !

