齿轮的改进：渐开线齿轮和正负变位

齿轮的历史

齿轮可以定义为齿形轮，它将旋转力传递到另一个齿轮或装置，以传输能量，从而改变速度和运动方向，并完全转移力而不产生滑移，其角速度均匀。

早在公元前350年，古希腊著名的哲学家亚里士多德在文献中对齿轮有过记录。公元前250年左右，数学家阿基米德也在文献中对使用了涡轮蜗杆的卷扬机进行了说明。在现今伊拉克凯特斯芬遗迹中还保存着公元前的齿轮。齿轮在我国的历史也源远流长。据史料记载，远在公元前400~200年的中国古代就已开始使用齿轮，在我国山西出土的青铜齿轮是迄今已发现的最古老齿轮，作为反映古代科学技术成就的指南车就是以齿轮机构为核心的机械装置。

直到17世纪末，人们才开始研究能正确传递运动的轮齿形状。18世纪，欧洲工业革命以后，齿轮传动的应用日益广泛；先是发展摆线齿轮，而后是渐开线齿轮，一直到20世纪初，渐开线齿轮已在应用中占了优势。其后又发展了变位齿轮、圆弧齿轮、锥齿轮、斜齿轮等等。

现代齿轮技术已达到：齿轮模数0.004~100毫米；齿轮直径由1毫米~150米；传递功率可达十万千瓦；转速可达十万转/分；最高的圆周速度达300米/秒。国际上，动力传动齿轮装置正沿着小型化、高速化、标准化方向发展。特殊齿轮的应用、行星齿轮装置的发展、低振动、低噪声齿轮装置的研制是齿轮设计方面的一些特点。

齿轮的术语和尺寸

齿轮部位名称；模数；压力角；齿高和齿厚；齿轮直径；中心距和齿隙；斜齿齿轮；螺旋方向和配合。

部位名称：

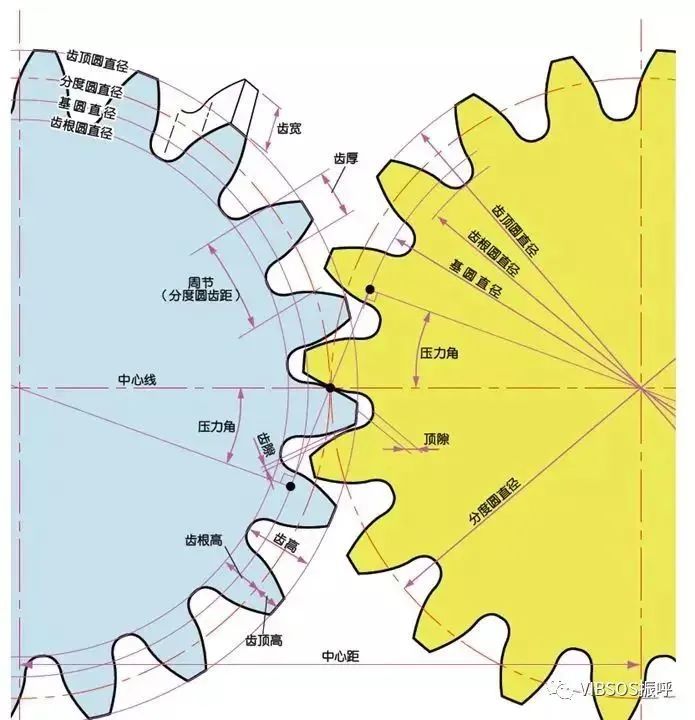
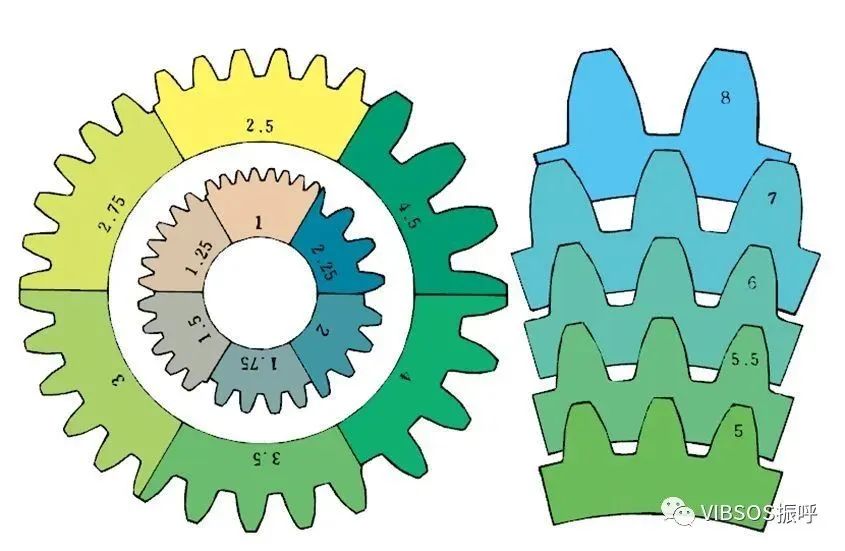
模数：

使用符号m（模数）和数字（毫米〉来表示轮齿的大小，数字越大，轮齿也越大。模数乘以圆周率即可得到齿距（p），齿距是相邻两齿间的长度。

p=圆周率x模数= πm。

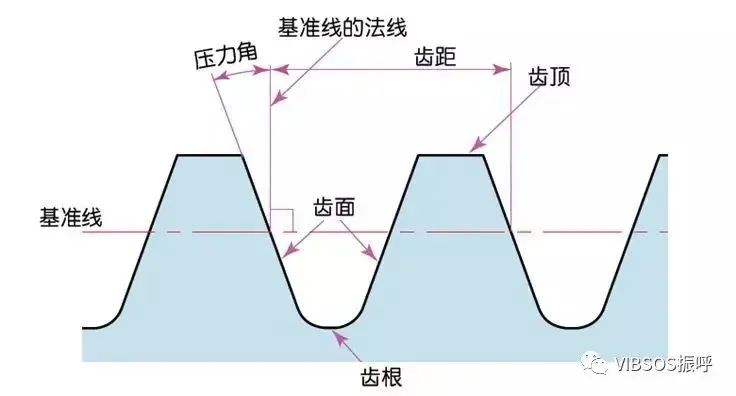
压力角：

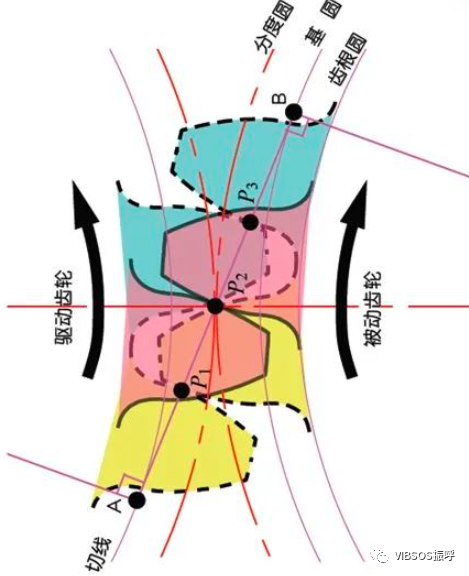
压力角是决定齿轮齿形的参数。即轮齿齿面的倾斜度。压力角（α）一般采用20°。以前，压力角为14.5°的齿轮曾经很普及。压力角是在齿面的一点（一般是指节点）上，半径线与齿形的切线间所成之角度。如图所示，α为压力角。因为α’=α，所以α’也是压力角。

 

 

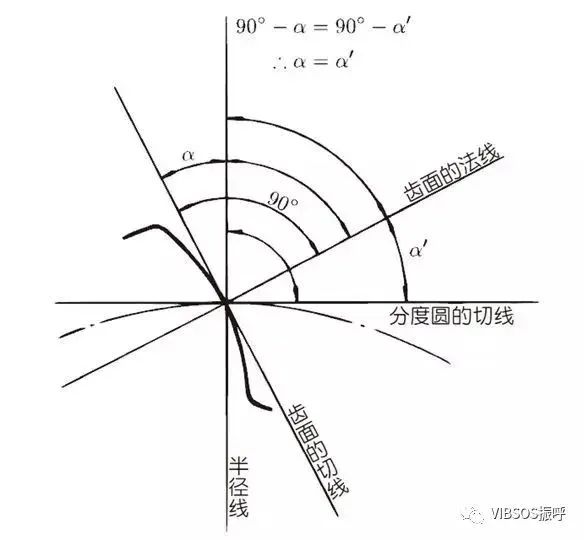
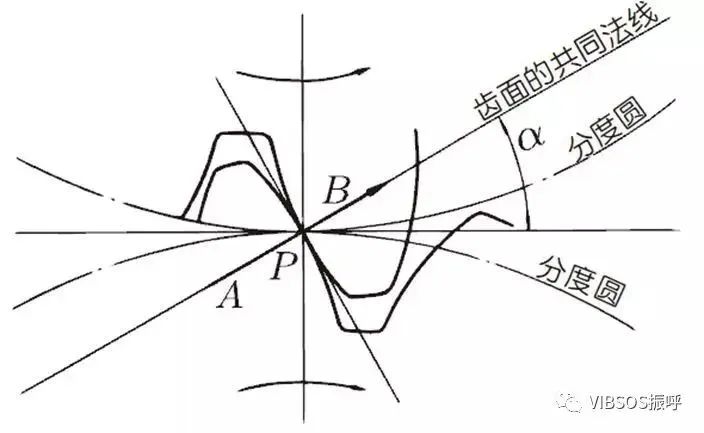
A齿与B齿的啮合状态从节点看上去时：A齿在节点上推动B点。这个时候的推动力作用在A齿及B齿的共同法线上。也就是说，共同法线是力的作用方向，亦是承受压力的方向，α则为压力角。

齿高和齿厚：

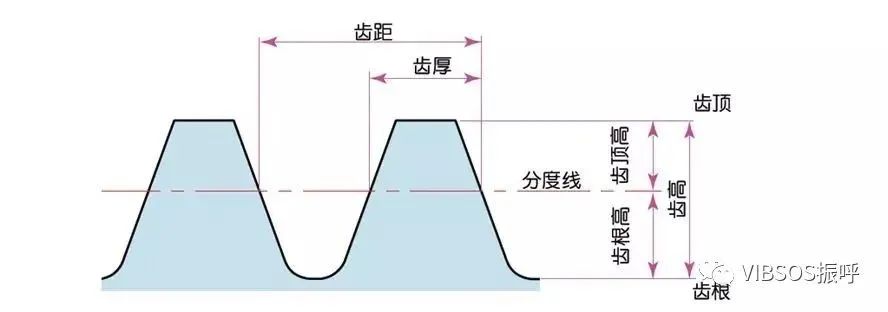
全齿高 h=2.25m（=齿根高+齿顶高）

齿顶高（ha）是从齿顶到分度线的高度。ha=1m。

齿根高（hf）是从齿根到分度线的高度。hf=1.25m。

齿厚 （s）的基准是齿距的一半。s=πm/2。

齿轮的直径：

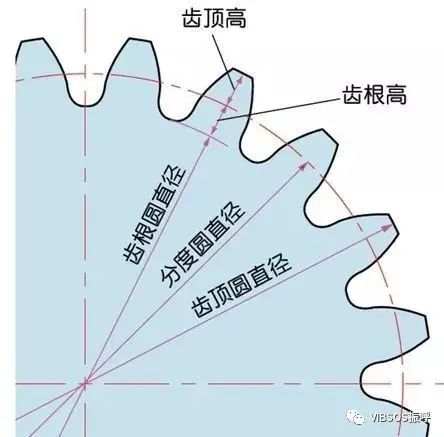
决定齿轮大小的参数是齿轮的分度圆直径（d）。以分度圆为基准，才能定出齿距、齿厚、齿高、齿顶高、齿根高。分度圆在实际的齿轮中是无法直接看到的，因为分度圆是为了决定齿轮的大小而假设的圆。

分度圆直径 d=zm

齿顶圆直径da=d+2m

齿根圆直径df=d-2.5m

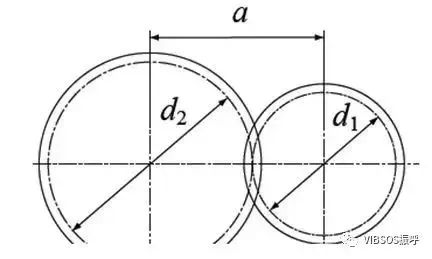
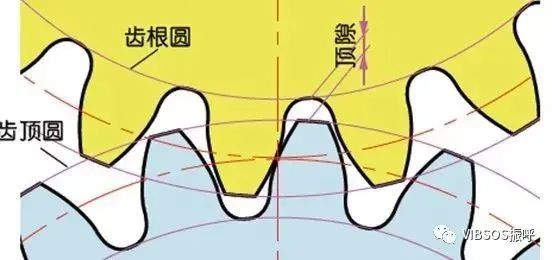
中心距和齿隙：

一对齿轮的分度圆相切啮合时，中心距是两个分度圆直径的和的一半。中心距a=（d1+d2）/2。

在齿轮的啮合中，要想得到圆滑的啮合效果，齿隙是个重要的因素。齿隙是一对齿轮啮合时齿面间的空隙。齿轮的齿高方向也有空隙。这个空隙被称为顶隙（Clearance)。顶隙(c)是齿轮的齿根高与相配齿轮的齿顶高之差。顶隙c=1.25m-1m=0.25m。

斜齿齿轮：

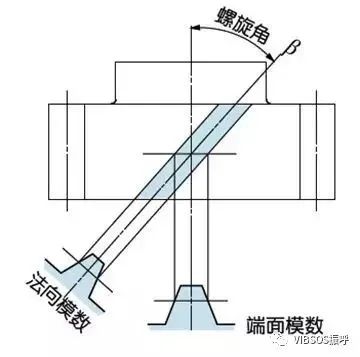
将正齿轮的轮齿螺旋状扭转后的齿轮为斜齿齿轮。正齿轮几何计算的大部分都可适用于斜齿齿轮。斜齿齿轮，根据其基准面不同有2种方式：

端面（轴直角）基准（端面模数/压力角〉；

法面（齿直角）基准（法向模数/压力角〉；

端面模数mt和法向模数mn的关系式mt=mn/cosβ

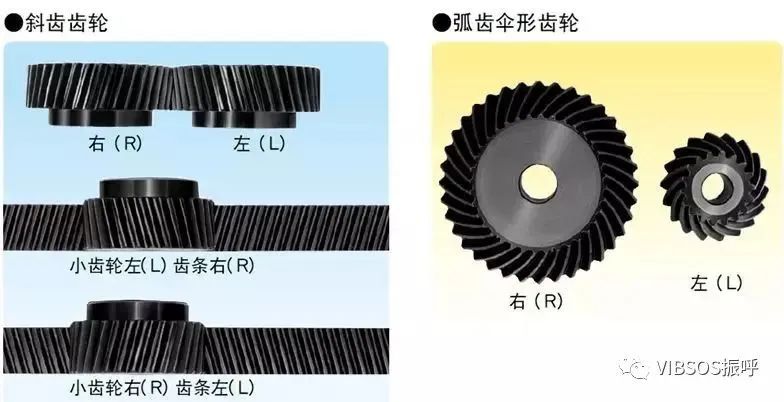
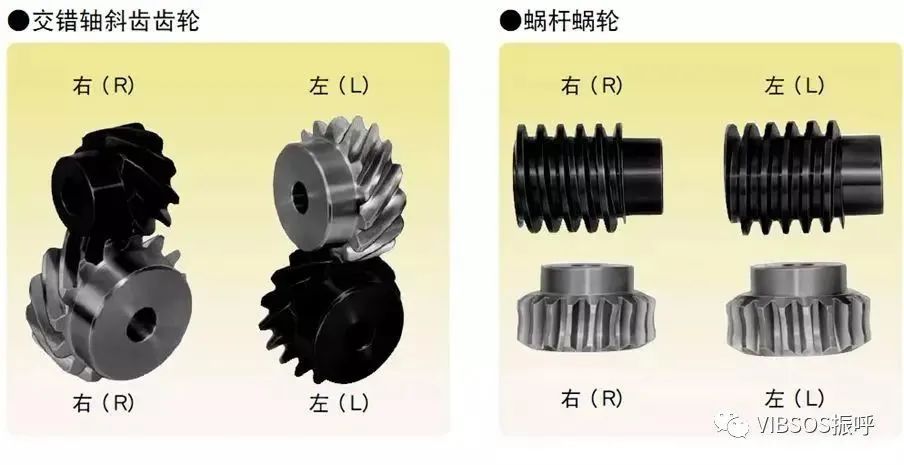
螺旋方向与配合：

斜齿齿轮、弧齿伞形齿轮等，轮齿呈螺旋状的齿轮，螺旋方向和配合是一定的。螺旋方向是指当齿轮的中心轴指向上下，从正面看上去时，轮齿的方向指向右上的是“右旋”，左上的是“左旋”。各种齿轮的配合如下所示。

 

齿轮的计算公式

标准正齿轮的计算（小齿轮①，大齿轮②）见下图，其他可参考。

齿轮的改进

渐开线齿轮；正负变位。

仅仅在摩擦轮的外周上分割出等分的齿距，装上突起，然后相互啮合转动的话,会出现如下问题：

轮齿的切点产生滑动

切点的移动速度时快时慢

产生振动及噪音

轮齿传动时既要安静又要圆滑，由此，诞生了渐开曲线。

将一端系有铅笔的线缠在圆筒的外周上，然后在线绷紧的状态下将线渐渐放开。此时，铅笔所画出的曲线即为渐开曲线。圆筒的外周被称为基圆。示例：将圆筒8等分后，系上8根铅笔，画出8条渐开曲线。然后，将线向相反方向缠绕，按同样方法画出8条曲线，这就是以渐开曲线作为齿形，齿数为8的齿轮。

基圆是形成渐开线齿形的基础圆。分度圆是决定齿轮大小的基准圆。基圆与分度圆是齿轮的重要几何尺寸。渐开线齿形是在基圆的外侧形成的曲线。在基圆上压力角为零度。两个标准的渐开线齿轮的分度圆在标准的中心距下相切啮合。两轮啮合时的模样，看上去就像是分度圆直径大小为d1、d2两个摩擦轮（Friction wheels）在传动。但是，实际上渐开线齿轮的啮合取决于基圆而不是分度圆。

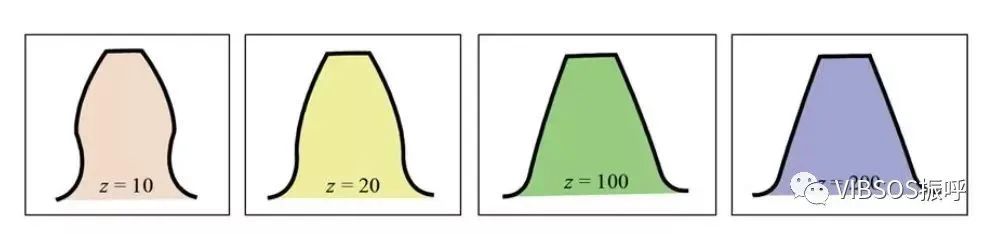
我们通常使用的齿轮的齿廓一般都是标准的渐开线，然而也存在一些情况需要对轮齿进行变位，如调整中心距、防止小齿轮的根切等。渐开线齿形曲线随齿数多少而不同。齿数越多，齿形曲线越趋于直线。随齿数增加，齿根的齿形变厚，轮齿强度增加。由上图可以看到，齿数为10的齿轮，其轮齿的齿根处部分渐开线齿形被挖去，发生根切现象。但是如果对齿数z=10的齿轮采用正变位，增大齿顶圆直径、增加轮齿的齿厚的话，可以得到与齿数200的齿轮同等程度的齿轮强度。变位有正变位和负变位。虽然齿高相同，但齿厚不同。齿厚变厚的为正变位齿轮，齿厚变薄的为负变位齿轮。

齿轮的精度

保证动力传递；体积小；低噪低振；精度高。

齿轮的精度大致可以分为三类：

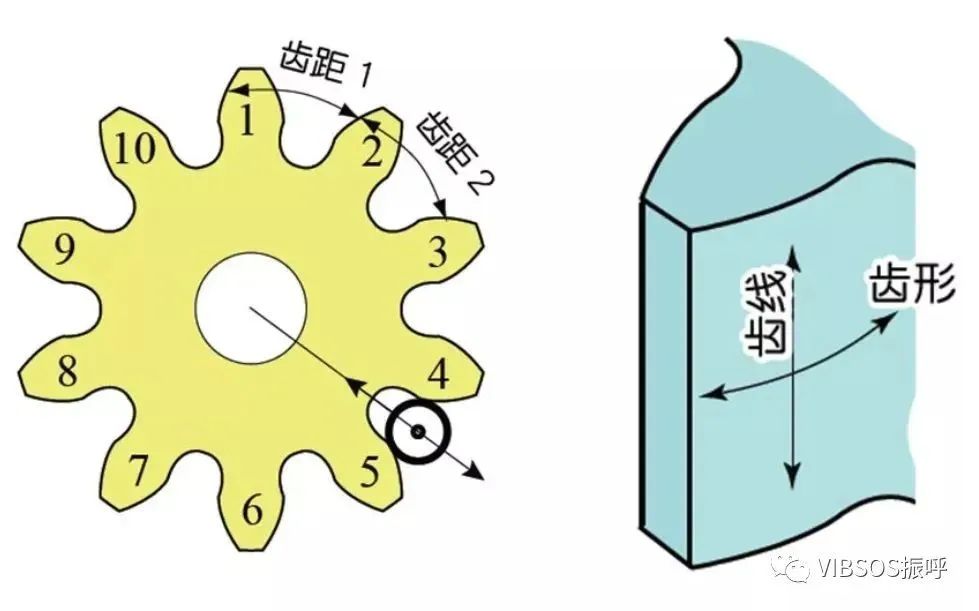
a）渐开线齿形的正确度—齿形精度

b）齿面上齿线的正确度—齿线精度

c）齿/齿槽位置的正确度

轮齿的分度精度——单齿距精度

齿距的正确度——累积齿距精度

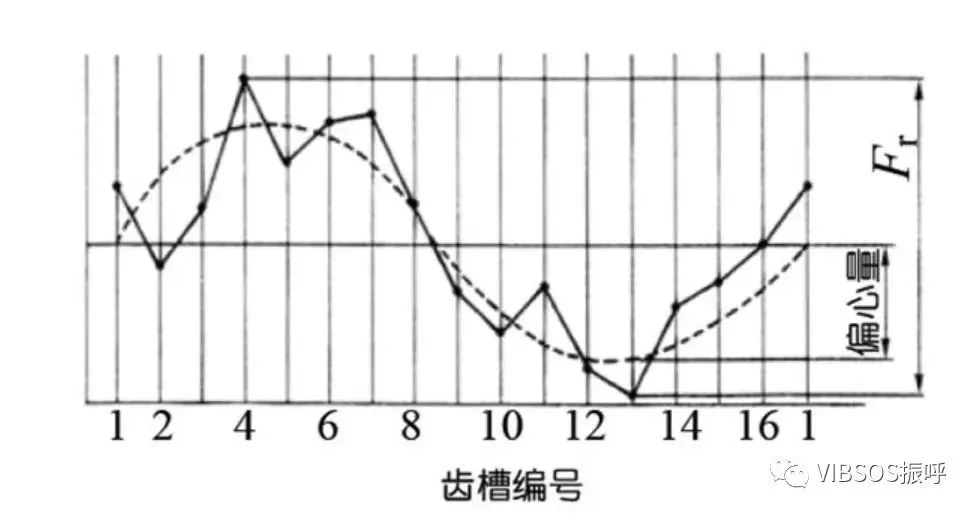
夹在两齿轮的测球在半径方向位置的偏差——径向跳动精度

 

 

 

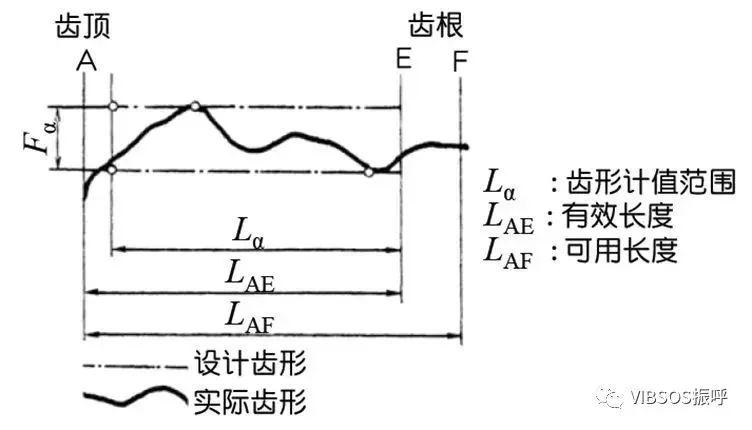
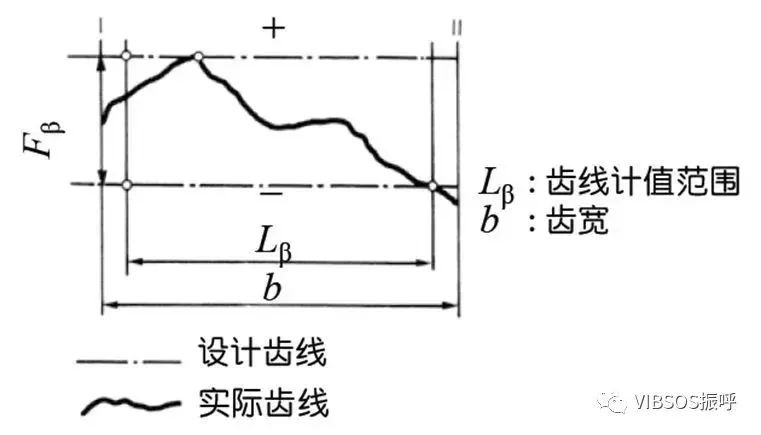
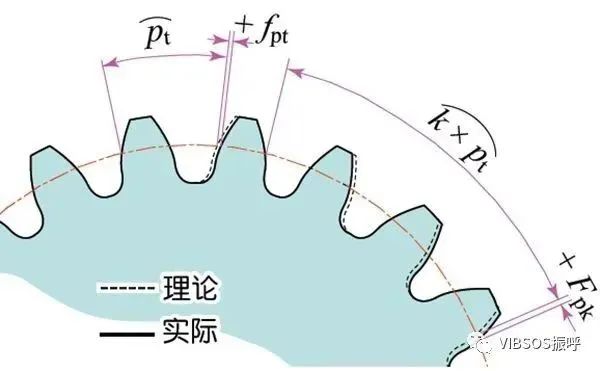
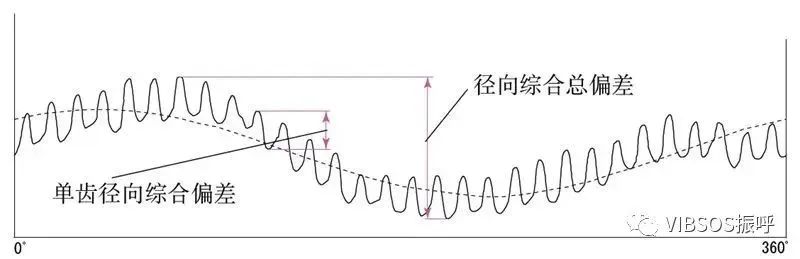
径向跳动（Fr，将测头（球形、圆柱形）相继置于齿槽内，测定测头到齿轮轴线的最大和最小径向距离之差。齿轮轴的偏心量是径向跳动的一部分。）；径向综合总偏差（Fi，被测齿轮的左右两齿面与测量齿轮接触啮合，并旋转一整周。记录中心距离的变化。）

 

高精度齿轮的条件

   

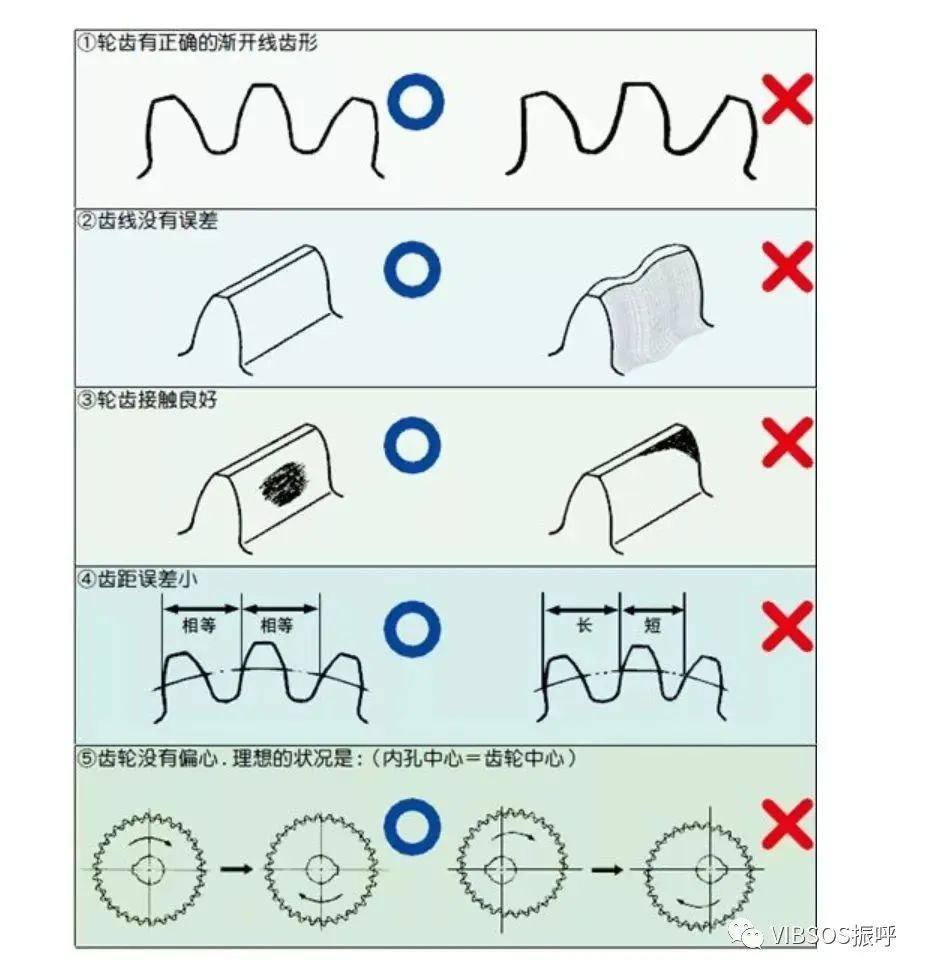
编辑：黄飞