

微纳米电子器件的散热流程和机理
制造/封装
描述
摘要
微纳米电子器件的散热问题是目前制约半导体工业发展的重要瓶颈。将电子器件工作时产生的热量传输到封装外壳后再耗散到环境中去需要好几个步骤,每个步骤需要不同的方法,其中有些步骤涉及到了固体中的界面热传导问题和高性能导热材料。文章先介绍了近期关于微纳米尺度器件散热问题中碰到的热传导问题在理论和实验两方面的研究进展。在热传导理论和计算方法方面,作者讨论了傅里叶定律在微纳米尺度的适用性,介绍了玻尔兹曼方程、分子动力学模拟和格林函数方法。在热传导实验方面,介绍了用扫描热显微镜测量样品表面温度和用超快激光反射法测量薄膜材料的热导率及其界面热阻。然后介绍了界面热传导问题,包括界面热阻的计算以及电子—声子相互作用对界面热阻的影响。最后作者介绍了关于高性能导热材料方面的最新进展,包括碳基导热材料、晶格结构类似于石墨烯的氮化硼材料、高分子有机材料以及界面热阻材料。
关键词:微纳米器件,散热,热导率,界面热阻,电子—声子相互作用
01 引言
随着科学技术的进步,半导体集成电路的器件集成度按照摩尔定律(Moore’s law)快速增加, 目前普遍采用的22nm晶体管生产工艺可以在一平方厘米的面积内集成数十亿个晶体管。如此密集的晶体管在以极高频率工作时必然会产生巨大的热量,包括晶体管中电流通过时产生的焦耳热和电容充放电时所产生的热量。
这些热量积聚在极小的器件范围内,如果不及时疏导出去,会使得电子器件的局部温度急剧升高,形成热点(hot spot)。过高的温度会大大降低器件的可靠性和运行速度,并最终导致集成电路被烧毁。因此,将产生的热量及时耗散到器件以外,使器件的工作温度保持在较低水平是半导体电子工业发展所面临的一个重要课题。
总体上说,大规模集成电路的散热大致上可以分为两个(或者三个)步骤,如图1(a)所示。第一步是单个晶体管产生的热量被传导通过封装外壳。第二步是通过多种介质将热量从封装外壳扩散到环境中,例如目前计算机中普遍采用的是以空气为介质的气冷方式,即风扇或散热片,如图1(b)所示;以液体为介质的液冷方式,如微槽道冷却结构(micro-channel cooling);以电子—声子为介质的热电制冷(thermo-electric cooling)等等。
对于某些特大型的电子设备,如超级计算机和大型数据中心,则需要增加第三个步骤,将热量从室内环境耗散到室外环境,通常使用空气调节系统来实现。
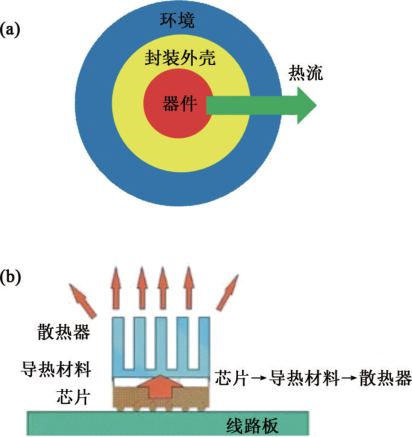
图 1(a)集成电路散热流程示意图 ;(b) 通过空气对流的散热片工作原理
本文讨论电子器件内部以及器件与封装外壳之间的固体散热所涉及到的物理问题,主要包括界面热阻问题和高性能导热材料的研究。由于气冷和液冷属于流体力学和工程热物理范畴,在本文中不予讨论,而关于热电效应散热和如何将余热转换成电在本期杂志中有另外一篇文章专门讨论。
02 微纳米尺度的热传导理论与计算方法
微纳米尺度热传导理论所面临的问题有很多尚待解决,主要有以下几个方面:
(1)温度的定义问题。温度在宏观体系中是很直观的,它是通过一个宏观上足够小而微观上足够大的范围内的原子运动达到热平衡时的平均动能来定义的。但是,在微纳米尺度下,是否能够找到这样一个定义局域温度的空间范围是有疑问的,有可能整个微纳米器件的空间体积都太小,以至于无法定义出温度。
(2)关于热导率定义的问题。通常热导率是根据傅里叶定律定义的:
J =-κ∇T,(1)
其中 J 是热流密度,κ是热导率,∇T是温度梯度。热流密度是单位时间内通过单位面积的热量,因此定义热流通过的面积是定义热导率的先决条件。热流通过的面积在三维材料中可以很容易定义,而在一维材料和二维材料中很难严格定义。
以一维碳纳米管和二维石墨烯为例,人们通常将碳纳米管的圆形横截面的面积和石墨烯的单层原子厚度的矩形横截面的面积作为热流通过的面积,得到了比一般三维材料高得多的热导率。
而实际上,如果将碳纳米管和石墨烯堆砌成三维材料,由于原子间存在的排斥作用力,碳纳米管的管与管之间的距离要比管的直径大很多,石墨烯的层与层之间的距离也远大于单层原子的厚度。
因此,堆砌后每根碳纳米管和每层石墨烯内通过的热流面积应该既包括材料本身的横截面积,也包括堆砌时产生的空隙的横截面积,这样得到的热导率就会变小,如此才能真正和三维材料进行比较。
总而言之,一维和二维材料的热导率应该和将它们堆砌成三维材料时的堆砌密度(packing density)紧密相关。
另外须要指出的是,傅里叶定律描述的是一个线性响应的输运过程,在微纳米尺度下,热输运常常是非线性的,即热流密度并不正比于温度梯度,而且有可能与样品的尺寸有直接关系,此时用-J/∇T来定义热导率是不严格的。
(3)连续介质模型的适用性。目前的半导体电子器件的尺寸已经普遍小于100nm的量级,而固体中热流的主要载体之一——短波(大波矢)声子——在室温下的平均自由程大致在1nm到100nm之间。
当电子器件的尺寸和声子的平均自由程以及声子的波长可以比拟的时候,原先使用的在连续介质中得到的热传导理论(如玻尔兹曼方程)还是否适用是一个无法回避的问题,到目前为止,还没有足够完善的理论能够很好地处理声子的波动性对热传导的影响。下面我们介绍几种常用的计算材料导热性能的理论和方法。
2.1 玻尔兹曼方程
玻尔兹曼方程是最常见的计算固体中的输运性质的理论,用它可以计算电子和声子的各种输运性质,例如电导率、热导率、热电系数等,方程的形式和各种散射机制已经被深入而系统地研究。
对于微纳米器件,当器件的尺寸与载流子(电子或声子)的波长和平均自由程可以比拟时,玻尔兹曼方程的适用性就会受到怀疑。因为玻尔兹曼方程是将载流子当做粒子来处理的,属于连续介质理论,波动性并没有被考虑进来。此外,玻尔兹曼方程主要针对扩散区的输运,当微纳米器件的尺寸微小到载流子必须做弹道输运时显然是不适用的。
这一困难至今未被很好地解决,不过这并不阻碍人们使用玻尔兹曼方程来近似计算热导率。
微纳米结构对声子输运的重要影响主要包括改变声子的色散关系(dispersion relation)以及其结构界面对声子的散射。
Yang 和 Chen 通过直接求解声子玻尔兹曼方程的方法研究了多种规则的纳米材料的导热性质。他们发现,在核心—外壳(core—shell)结构复合纳米线和中空的管型(tubular)纳米线中,热导率不仅与材料本身相关,还与纳米线的半径和空管内壁的半径有关,这一现象来源于声子的弹道输运现象,即当样品的尺寸小于声子散射的平均自由程时,声子将会以弹道飞行的方式传播。这一现象为人们提供了一种调控纳米材料导热性质的手段。他们还将纳米线嵌入块体材料中,形成周期性二维纳米混合物(nanocomposites)。计算结果显示,在纳米线材料所占体积比(volumetric fraction)相同的情况下,沿纳米线方向的热导率随纳米线半径的减小而减小。
Lacroix等人研究了不同厚度的硅和锗薄板的声子输运性质。Prasher研究了多空材料中微纳米尺度的微孔对热导率的削弱作用。
对于某些形状不规则的三维纳米结构材料,由于计算的复杂度太高,玻尔兹曼方程是很难直接求解的,用蒙特卡罗方法来模拟声子的输运过程,从而求解声子玻尔兹曼方程是一种比较理想的选择。例如,Jeng 等人利用蒙特卡罗方法模拟计算了纳米颗粒混合物(nanoparticle composites)中的热导率,发现纳米颗粒的尺寸大小以及纳米颗粒物所占的体积比例对声子输运有重要影响。
2.2 分子动力学方法
分子动力学(molecular dynamics, MD)方法是利用牛顿运动方程来模拟相互作用的分子或原子体系的运动,然后使用Green—Kubo 方法计算出热导率,或者在模拟时在样品两端加温度差,再用傅里叶定律直接得出热导率。人们利用分子动力学方法研究了很多纳米尺寸材料的导热性质,如碳纳米管、纳米线、石墨烯纳米条带等。此外,分子动力学方法也可以用于研究不同材料形成界面时的界面热导。
在界面附近大约若干纳米的范围内,原子会杂乱无章地混合在一起,如图 2 所示,人们可以通过分子动力学方法模拟得到界面处的原子分布及其振动情况,然后用其他手段获得导热性质。
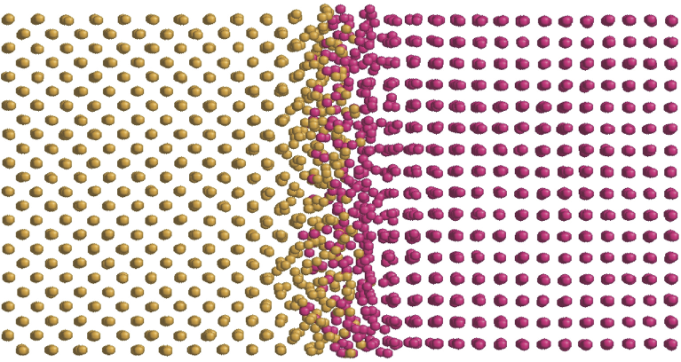
图2 由分子动力学模拟得到的界面附近两种原子的杂乱分布
需要指出,分子动力学方法完全是经典的,不涉及量子力学问题,所使用的原子之间的相互作用势通常是经验势(如Tersoff势,Brenner势等),而且电子的运动不能被包括进来,因此无法计算电子对热导率的贡献,也无法考虑电子—声子相互作用。另外,分子动力学方法属于原子尺度的模拟,如果用它来模拟微纳米器件,计算量将超出目前计算机所能承受的范围,因此对于更大尺度的热输运计算还是要用玻尔兹曼方程(见2.1节)。
2.3 格林函数方法
原子格林函数(atomic Green’s function, AGF)方法是在获知样品的原子分布以及所有原子之间的相互作用势以后,通过求解简谐近似下的声子动力学方程来计算热导的一种方法,它也是一种原子尺度的计算工具。原子格林函数G是原子体系对微小扰动的响应函数,它的定义为
(ω2I - H)G = I, (2)
其中ω是晶格振动的角频率, I 是单位矩阵,H是简谐矩阵。对于给定的原子体系,可以写出其对应的简谐矩阵,通过对(2)式左边括号内的矩阵求逆可以得到格林函数G。在得到G之后就可以得到样品一端到另一端的响应,然后计算出声子通过界面的透射系数随角频率的变化,从而进一步计算出热导率。
Mingo和Yang利用原子格林函数方法计算了被非晶材料包裹的硅纳米线中的声子输运。Zhang等人计算了通过纳米线结的热传导性质。原子格林函数还被广泛应用于界面热传导的计算中,例如晶格匹配的应变硅/锗界面和晶格不匹配的硅/锗界面。
除原子格林函数以外,还有很多不同的格林函数方法被用来计算热导率,例如,Yamamoto 和 Watanabe发展了一套非平衡声子格林函数方法,并用它计算了有缺陷的碳纳米管的声子输运。
03 微纳米尺度的热传导实验
微小的尺寸和复杂的结构也给实验观测带来很大的困难,传统的测量热流和温度的方法并不适用,需要发展一些新的实验手段,我们下面介绍两种近来比较常用的实验方法。
3.1 扫描热显微镜 (scanning thermal microscopy,SThM)
扫描热显微镜的工作原理是将一个热敏针尖靠近被测的固体样品表面,样品表面与针尖的热交换会使得针尖的温度升高。通过针尖扫描整个样品表面,可以得到针尖—样品的热交换的空间分布关系,由此可以探测出样品表面的温度分布情况。目前,SThM 主要利用原子力显微镜(atomic force microscope, AFM)这一实验平台来实现。
3.2 超快激光反射测温法
超快激光热反射技术(ultrafast thermo-reflectance techniques) 包括时域热反射(time-domain thermoreflectance, TDTR)和最近发展起来的频域热反射(frequency-domain thermoreflectance, FDTR)两种。以TDTR为例,将亚皮秒激光波包分成两束照射在三层结构的样品上,样品的第一层的作用是吸热和传感,第二层为待测样品,第三层为衬底。第一束泵浦激光将样品加热,第二束探测激光探测样品的反射率或者衍射信号的变化。不停地重复这一泵浦—探测过程,并改变探测激光与泵浦激光之间的时间间隔,通过求解热扩散模型,拟合探测信号随时间间隔变长后的衰减,就能得出薄膜材料的热导率和与衬底之间的界面热导。由于亚皮秒激光波包的时域内对应的热扩散长度在纳米量级,因此TDTR可以直接测量纳米尺度的热扩散过程。
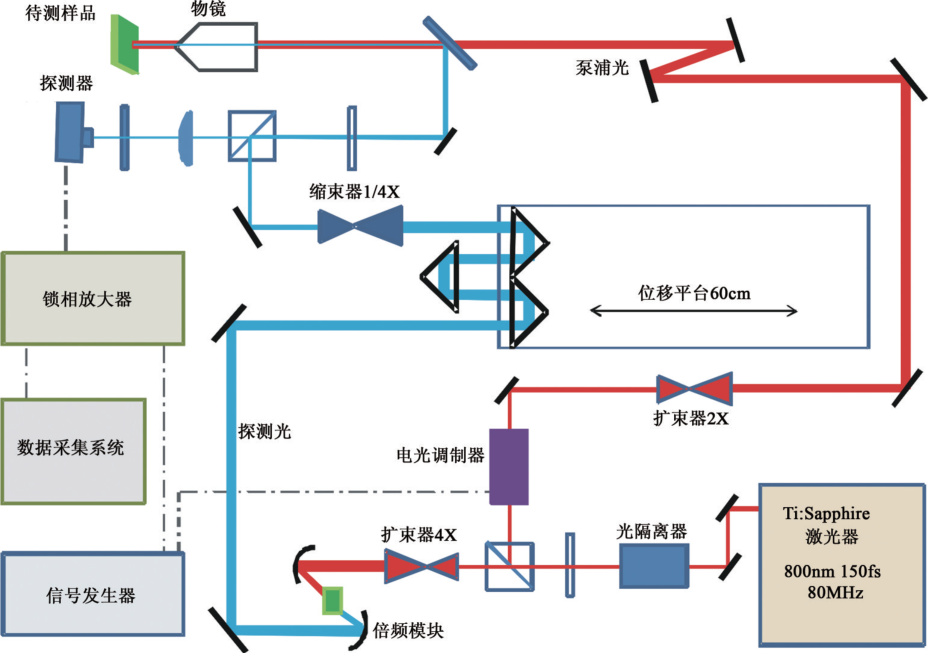
图3 Zhu等人用于超快激光泵浦—探测热反射实验的光路示意图
图3是典型的超快激光热反射系统的光路图,激光波包由钛—蓝宝石飞秒激光器产生,在激光波包被分成泵浦光和探测光后,将探测光的频率倍增后导入机械移动模块,用以调节泵浦光与探测光之间的时间间隔,从而实现双色光探测系统。
FDTR 与 TDTR 十分类似,只是将探测激光与泵浦激光的时间间隔固定,对不同的激光调制频率(modulation frequency,即单位时间内的波包数目)做一系列的探测,同样可以求解热扩散模型后拟合出界面热导。图 3 所示的光路可以同时用于TDTR和FDTR的探测。
04 界面热传导问题
界面对纳米尺度的热传导具有重大的影响,尤其是在集成电路设计时,引入过多界面会使得电路内部形成很多热点,从而加剧器件的发热。由于界面两侧材料与结构的差异,声子在穿越界面时会受到散射,界面两侧的局域温度会发生跳跃ΔT。由此可以定义界面热阻 (thermal boundary resistance, TBR)或者卡皮查热阻(Kapitza resistance):
R=∆T/Q , (3)
其中Q是流过界面的热流密度,界面热阻的倒数一般被称为界面热导。
4.1 界面热阻的计算方法
经典的估算界面热阻的方法是声学不匹配模型(acoustic mismatch model, AMM)和扩散不匹配模型(diffuse mismatch model, DMM)。
对于理想的界面,其两侧材料的声速和质量密度的差异会导致声学阻抗(acoustic impedance)的不匹配,AMM 忽略界面本身对声子的散射,认为声子从材料 1 垂直入射经过界面进入材料 2 的透射系数 t12只与声学阻抗相关:
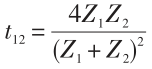 ,(4)
,(4)
其中 Z=ρc 为声学阻抗,ρ为质量密度,c为声速。由于AMM并不考虑界面对声子的散射,而这种散射会打开新的能量传输通道,因此考虑散射后得到的界面热阻会比 AMM 得到的界面热阻小。DMM 给出的是考虑了散射后的极端情况,DMM假设所有的声子都被界面所散射,而且声子在散射后完全失去对散射之前的记忆。从材料 1 中入射的声子与材料 2 中出射的声子没有任何声学关联,声子的透射和反射几率只与声子态密度(phonon density of states)有关。
由于 AMM 和 DMM 的假设都过于简单,而实际的界面问题远比这些假设要复杂得多。利用 2.1 节中介绍的玻尔兹曼方程,2.2节中介绍的分子动力学方法和2.3节中介绍的格林函数方法来计算界面热阻要比AMM和DMM更为有力。
4.2 电子—声子相互作用对界面热阻的影响
电子对界面热阻的影响也是一个重要问题,目前的实验已经证明,在计算金属/非金属界面的热导时必须考虑界面处的电子—声子相互作用,例如Guo等人利用TDTR方法测量了金—硅样品界面处的界面热导,验证了金中的电子与硅中的声子具有很强的直接相互作用。
在金属(或者重掺杂半导体)中,电子是主要的热载流子,而在非金属中,声子是主要的热载流子。当热流流过金属/非金属界面时,金属一侧的电子和声子之间会产生不平衡,即金属中的电子温度 Tm,e和晶格温度 Tm,p不相等,在金属内部就会发生电子和声子的能量交换。
特别地,金属中的电子会在界面附近将能量直接传给非金属中的声子,形成一个新的能量输运通道,可以定义另一种有别于 (3) 式的由电子—声子相互作用导致的界面热阻Re:
Re=(Tm,e-Tn,p)/Q', (5)
其中Tn,p为非金属中的晶格温度,Q'是界面处电子—声子相互作用引起的能量交换。
目前对于这方面的理论研究还不是很多,Huberman和Overhauser通过计算金刚石/铅界面附近声子的组合振动模(joint vibrational modes)与金属中自由电子的相互作用,然后用费米黄金规则计算出电子—声子相互作用导致的界面热阻。他们计算得到的室温下的结果与实验测得的结果是一致的。
Sergeev认为,金属/非金属界面处的电子—声子相互作用可以类比于非弹性的电子—杂质散射,因为它们都是局域化的散射,且电子的动量损失都很大。
Mahan提出了另一种界面附近的电子—声子相互作用机制,如果非金属材料是极化材料的话,金属表面的静电荷会在非金属材料内形成一个镜像电势,当非金属材料中的离子振动时,电荷密度发生振荡,离子振动就会和电子发生直接耦合。
通过进一步的分析,我们认为,在得到界面处的电子—声子相互作用形式之后,并不能像上述几个工作那样,用它来直接计算界面热导。在考虑金属/非金属界面的热输运时,电子和声子分别会被界面散射,而电子和声子始终是耦合在一起的。因此在计算热输运时,应该统一考虑电子和声子的耦合输运,包括金属内部以及界面附近的电子—声子相互作用,而不应该分开单独考虑。
Majumdar和Reddy用简单的两温度模型考虑了金属中的电子—声子相互作用对界面热导的影响,该模型基于傅里叶定律和金属中的能量平衡方程:
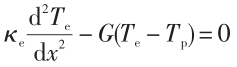
, (6)
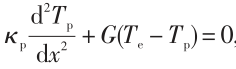
, (7)
其中 Te为电子温度,Tp为声子温度,κe为电子热导率,κp为声子热导率,G 为电子—声子耦合常数,其中假设电子—声子相互作用导致的能量转换率正比于电子温度与声子温度之差。通过选取适当的边界条件进行计算,他们发现,考虑了电子—声子相互作用后得到的界面热导比单独计算声子导致的界面热导要低,由此证明电子—声子相互作用的重要性。更进一步地,应该将界面处的电子—声子能量交换项一并引入到耦合输运的计算中来,但目前还没有看到这一方面的工作。
05 高性能导热材料
目前,半导体芯片中用于散热的导热材料还是以金属为主,以比较常见的铜为例,它的热导率约为 400W/m·K。除此之外,人们还在积极寻找新的高性能导热材料,下面我们介绍几类近来颇受关注的材料。
5.1 碳基材料
由碳原子组成的多种同素异形体(包括石墨、金刚石、碳纳米管(carbon nanotube)、碳60(C60)、石墨烯(graphene)等)是一类非常被看好的导热材料。它们的导热性能涵盖了很大的变化范围,从非晶碳的约 0.01W/m·K 到室温下金刚石的约2000W/m·K,再到碳纳米管的轴向热导率约3000—3500W/m·K。
近年来新发现的石墨烯材料是由单层碳原子组成的二维材料,其碳原子之间由 sp2轨道杂化形成的共价键连接在一起,呈六角蜂窝状晶格结构,如图 4 所示。
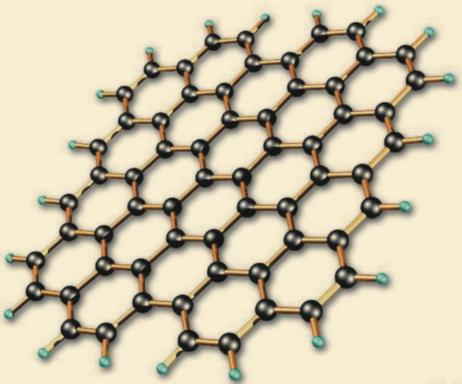
图4 石墨烯的六角形晶格结构
石墨烯材料由于其特殊的圆锥形电子能带结构而受到广泛的关注,同时石墨烯的导热性能也很好,有可能应用到未来的电子元件或声子元件中。目前关于石墨烯和石墨烯纳米条带的导热性能的研究已有不少,在本期的另一篇文章中将有详细介绍。
5.2 氮化硼纳米材料
氮和硼的原子序数分别比碳大一位和小一位,因此氮和硼原子可以组成类似于碳纳米管和石墨烯的结构,即氮化硼纳米管和氮化硼纳米网格(nanosheet)。这一类材料最近成为人们的研究热点,例如人们利用氮化硼纳米网格作为石墨烯衬底材料可以尽量减少衬底对石墨烯性质的影响。
氮化硼纳米管和氮化硼纳米网格本身也具有很高的热导率,前者随纳米管的长度变化,室温下大约为几十到上百 W/m·K,后者可以达到600W/m·K。
5.3 高分子有机材料
高分子有机材料有着非常广泛的应用前景,然而块体高分子有机材料较差的导热性质会严重阻碍这些应用。一般认为,块体高分子有机材料的热导率在室温下要比无机材料低很多,大约只有0.1-1W/m·K,其主要原因是高分子有机材料的分子链是随机绞在一起的,声子的平均自由程因此变得非常小。尽管块体高分子有机材料的热导率很低,但是单根有机分子链的热导率并不低,例如通过分子动力学模拟得到的一根100nm长的聚乙烯分子链的热导率高达 350W/m·K,这一模拟结果和实验测得的结果是一致的。
Liu和Yang通过分子动力学方法模拟了多种高分子链的热导率随分子链长度的变化情况,他们发现,所有分子链的热导率都随分子链变长而增加,而且不同材料的高分子链的热导率差距很大。另外,他们还发现在高分子链两端施加应力可以增加分子链的热导率。
5.4 热界面材料
从微观上看,在不同材料形成的界面处,固体表面的粗糙度会使界面附近充满空气,从而使实际的接触面积远小于界面的表面积。由于空气的导热性能很差,因此会极大地增加界面的整体热阻。为了减小这一不利因素的影响,人们通常在界面处填充具有较高导热系数的热界面材料(thermal interface materials, TIM)。
虽然热阻材料的使用会引入一个额外的界面,从而导致界面热阻的增加,但是由于可以形成一个比较畅通的导热通道,从总的效果来看可以减小界面的整体热阻。这类材料需要具有一定的变形性和流动性,从而尽可能地充满界面处的缝隙,增大接触面积。
比较常见的热界面材料有导热脂(thermal grease),它是将导热陶瓷填料(如氧化锌、二氧化硅等)加到硅树脂中或者烃油中后研磨成的膏状物;导热胶黏剂(thermal conductive adhesive),它是将导热填料(如氧化铝、碳化硅等)填充到硅树脂或者环氧树脂中形成胶黏剂;导热橡胶(thermal conductive elastomer),它由导热填料(如氧化铝、碳化硼、金属氧化物等)、硅橡胶和承载料(如玻璃纤维)组成;相变导热材料,它由石蜡、硅烷等高相变潜热材料加入导热填料组成。
除这些材料以外,人们还提出了一些其他类型的热界面材料,例如Lin等人提出利用碳纳米管—有机高分子纳米混合材料作为热界面材料。
06 结束语
本文回顾了微纳米电子器件的散热流程和机理,从理论和实验两个方面系统介绍了微纳米尺度固体热传导领域最新的研究进展。
理论方面,我们介绍了玻尔兹曼方程、分子动力学模拟和格林函数方法。实验方面,我们介绍了用扫描热显微镜测量样品表面温度和用超快激光反射法测量薄膜材料的热导率和界面热导。
然后详细讨论了界面热阻问题,指出电子—声子相互作用对界面热传导非常重要。我们进一步提出应该把电子输运和声子输运耦合起来处理金属/非金属界面的界面热阻问题。
最后我们介绍了几种最新的高性能导热材料:碳基材料如碳纳米管和石墨烯;与碳基材料具有类似晶格结构的氮化硼材料;有机高分子链,它和热导率很小的有机高分子块体材料不同,研究发现单根有机分子链具有很高的热导率;以及能够降低界面热阻的热界面材料。
编辑:黄飞
-
ESD对于电子器件的破坏机理分析2025-01-14 2786
-
电子器件散热技术解析与应用 | 氮化硼导热片2024-12-12 1320
-
高功率电子器件的散热方案2024-07-29 1995
-
高热流密度器件要怎么散热?你了解吗2024-07-25 1143
-
电子器件散热技术解析与应用考虑因素2024-05-20 1843
-
大功率电力电子器件散热研究综述2023-11-07 4409
-
电子元器件如何高效散热2022-10-31 2293
-
电子元器件的散热方法汇总2022-04-15 5031
-
光子器件与电子器件的性能有哪些不同2021-08-31 2633
-
电子器件的六种散热方法2020-06-20 22589
-
散热膏在电子器件中有什么作用2020-05-03 2844
-
电子元器件散热方法分析2019-08-27 3182
-
电力电子器件强制风冷用新型散热器的研究2017-09-14 950
-
电力电子器件课件2009-09-16 13376
全部0条评论

快来发表一下你的评论吧 !

