

讲解RC电路的零输入响应
描述
【动态电路】中无外施激励电源,仅有动态元件初始储能所产生的响应,称为动态电路的零输入响应,这个有点拗口,需要记住,这期介绍RC电路零输入响应,需要点一阶线性微分方程的基础。
关键词:串联RC电路;零输入响应;
01路结构
如图1-1所示,是RC电路的结构:
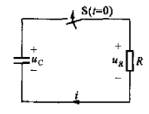
图1-1 RC电路
图1-1中,开关S闭合前,电容C已充电,其电容电压为U0,得已知条件为:
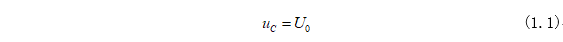
02分析思路
开关S闭合后,电容储存得能量将通过电阻以热能得形式释放出来,以开关动作为(t=0),那么开关闭合后,根据KVL可得:
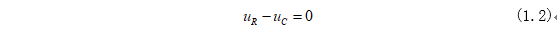
式(1.2)中电阻电压和电流为:
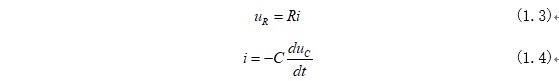
将式(1.3)和式(1.4)代入式(1.2)可得:
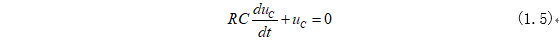
式(1.5)满足一阶齐次微分方程,这里不懂得可以回看【重拾数学基础】,列出其初始条件:
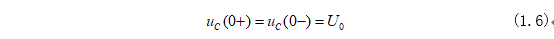
齐次方程的通解为:
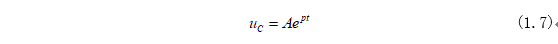
将式(1.7)代入式(1.5)可得:
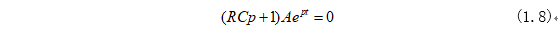
式(1.8)的 特征方程为:
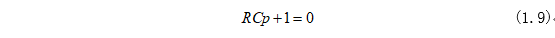
解式(1.9)可求得系数p为:
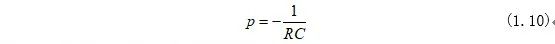
将式(1.6)代入式(1.7)可求得系数A:
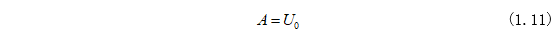
这样就求得满足初始值的微分方程的解为:
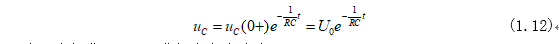
同时可以由式(1.12)求得电容电流为:
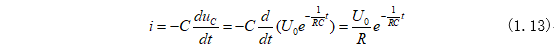
电阻上的电压就是电容上的电压为:
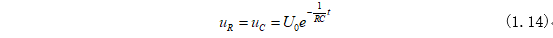
从式(1.12)、(1.13)、(1.14)可以看出,电容电压、电阻电压、电容电流都是按照同样的指数规律衰减的,其衰减快慢是由指数RC的倒数决定的,所以称RC的乘积为RC电路的时间常数。
时间常数RC的大小反映了一阶电路过渡过程的进展速度:
当t=0时,电容上的电压为:
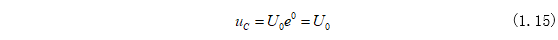
当t=RC时,电容上的电压为:
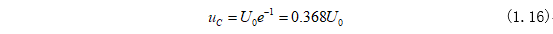
经过n个时间常数后,电容上电压如图1-2所示:

图1-2 衰减电压数值
工程上,一般认为换路后,经过3~5倍的时间常数,就认为过渡过程结束!
将图1-2表示的数值通过坐标表示,可如图1-3所示:
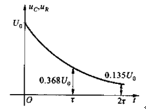
图1-3 衰减波形图
下期讲解RL电路的零输入响应!
-
什么是二阶电路的零状态响应和零输入响应?零输入响应的步骤有哪些?2023-11-21 4948
-
讲解RL电路的零输入响应2023-01-12 7514
-
浅谈RC电路的零状态响应2020-11-18 11660
-
RC电路与RL电路是如何响应的2020-10-06 13258
-
一阶RC电路的零输入响应与零状态响应的电路分析基础实验资料免费下载2019-05-27 5520
-
什么是rc一阶电路的零输出响应2017-11-01 19411
-
一阶电路的零输入响应2009-07-27 7896
-
论全响应和零状态响应、零输入响应2009-05-10 2365
-
一阶RC电路的暂态响应2008-12-17 1862
-
RC一阶电路的响应测试2008-09-24 75975
全部0条评论

快来发表一下你的评论吧 !

