讲解RC电路的零状态响应

【动态电路】的零状态响应就是电路在零初始状态下(动态元件初始储能为零)，由外施激励源引起的响应，与零输入响应不同的是，零状态响应内部储能在初始状态是零，就是储能元件初始储能为零，区分好这个后，就可以方便记住了，这期介绍RC电路的零状态响应，同样需要点一阶线性微分方程的基础!

关键词：RC电路;零状态响应;

01电路结构

如图1-1所示，是RC电路的结构：

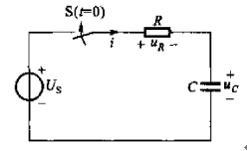
图1-1 RC电路零状态响应电路结构

图1-1中，开关S闭合前，电容C没有充电，其电容电压为0，得已知条件为：

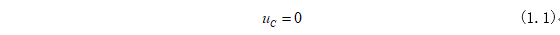
02分析思路

开关S闭合后，电容储存得能量将通过电阻以热能得形式释放出来，以开关动作为(t=0)，那么开关闭合后，根据KVL可得：

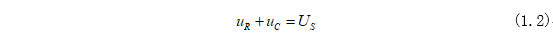
其中电阻电压和电容电流为：

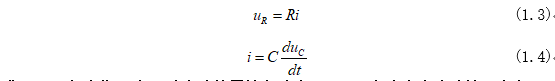
式(1.4)与上期那个一阶电路的零输入响应——RC电路中电流计算没有负号的原因是，图1-1电路电容电压为上正下负，电流i流进电容，给电容充电，上期电路相反，电流流出电容，电容充当电源。

将式(1.3)和式(1.4)代入式(1.2)可得电路的微分方程为：

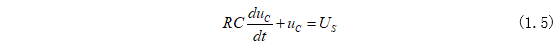
式(1.6)是一阶线性非齐次方程，方程的解由非齐次方程的特解和对应齐次方程的通解两个分量组成，这个在“重拾数学基础”中进行讲解了，忘记了可以再返回去看看!

其求解公式为：

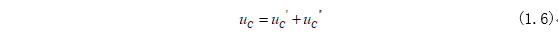
式(1.6)中等式右边第一项是非齐次方程的特解，第二项是齐次方程的通解。特解可以通过初始条件(1.1)代入式(1.5)可以求得非齐次方程的特解为：

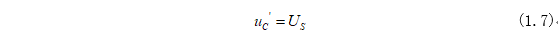
而齐次方程可根据上期“一阶电路的零输入响应——RC电路”的通解为：

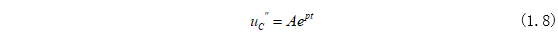
将式(1.8)中系数P换成时间常数为：

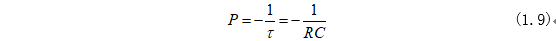
式(1.9)时间常数为RC，因此式(1.8)变为：

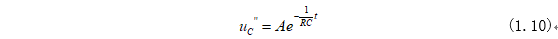
因此式(1.6)可根据式(1.8)和式(1.7)求得为：

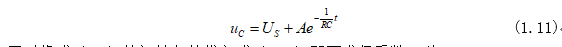
同时将式(1.1)的初始条件代入式(1.11)即可求得系数A为：

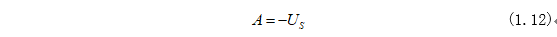
将式(1.12)代入式(1.11)因此式(1.11)可为：

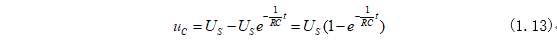
将电容电压进行求导即可求得电容电流i为：

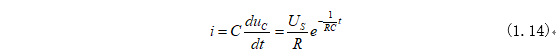
电路中电压、电流的波形如图1-2所示：

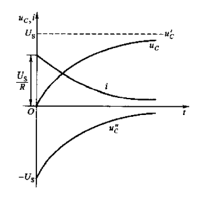
图1-2 电路电压、电流波形

图1-2说明，电容电压以指数形式趋近于它的最终恒定值Us，到达该值后，电压和电流不再变化，电容相当于开路，电流为零，此时电路达到稳定状态。RC电路接通直流电压源的过程也即是电源通过电阻对电容进行充电的过程。