

讲解RL电路的零状态响应
描述
【动态电路】的零状态响应就是电路在零初始状态下(动态元件初始储能为零),由外施激励源引起的响应,与零输入响应不同的是,零状态响应内部储能在初始状态是零,就是储能元件初始储能为零,区分好这个后,就可以方便记住了,这期介绍RL电路的零状态响应,同样需要点一阶线性微分方程的基础!
关键词:RL电路;零状态响应;
01电路结构
如图1-1所示,是RL电路的结构:
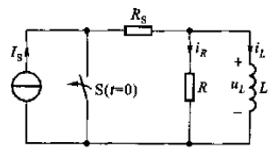
图1-1 RL零状态响应电路结构
图1-1所示为RL电路,直流电流源的电流为Is,在开关打开前电感L中电流为零,所以电感的初始条件为下:
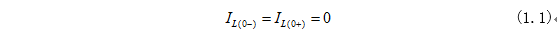
当电路稳定之后,电感相当于导线,把电阻R进行短路了,所以时间在无穷后,电感的电流为:
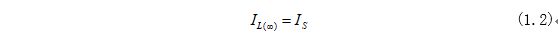
02分析思路
当开关S打开之后,电流源I对电感L就进行充电,电阻R两端的电压就是电感L两端的电压为:
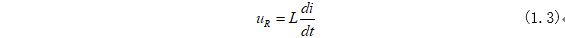
式(1.2)中电阻电压为正的原因是因为电流流进电感,给电感进行储能;上期“一阶电路的零输入响应——RL电路”同样需要根据电流方向来进行分析。
根据KCL可求得节点电流公式为:
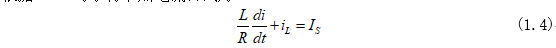
式(1.3)为非齐次微分方程,这里同“一阶电路的零状态响应——RC电路”一样,进行省略步骤,电流iL的通解为:
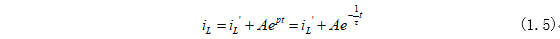
式(1.4)中右边第一项表示非齐次微分方程的特解,第二项表示齐次微分方程的通解。
特解可以根据根据电路的初始状态(1.1)代入式(1.5)进行求解为:
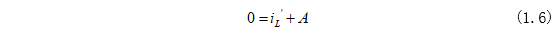
同时将电路稳定状态(1.2)代入代入式(1.5)进行求解为:
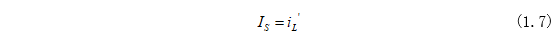
根据式(1.6)和式(1.7)可求得式(1.6)中系数A为:
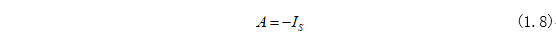
将式(1.7)和式(1.8)代入式(1.5)即可求得电路中电感电流为:
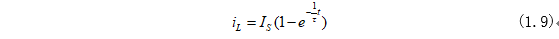
其中在开关S断开之后,RL电路的时间常数为:
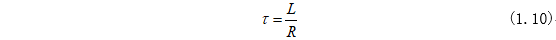
RL时间常数就是从电感L往外看的电路,将电流源断路,电压源短路后的等效电阻和自身电感比值的倒数。
将式(1.10)代入式(1.9)就可求得电感电流为:
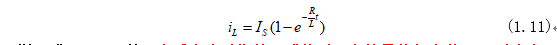
同样,式(1.11)说明电感电流以指数形式趋近于它的最终恒定值Is,到达该值后,电压和电流不再变化,电感相当于短路,电压为零,此时电路达到稳定状态。
-
什么是二阶电路的零状态响应和零输入响应?零输入响应的步骤有哪些?2023-11-21 4948
-
一阶RC和RL电路的0状态响应的区别在哪?2023-11-20 4561
-
讲解RC电路的零输入响应2023-01-12 8823
-
浅谈RC电路的零状态响应2020-11-18 11660
-
RC电路与RL电路是如何响应的2020-10-06 13258
-
一阶RC电路的零输入响应与零状态响应的电路分析基础实验资料免费下载2019-05-27 5519
-
零输入响应和零状态响应2009-09-10 3382
-
一阶电路的零状态响应2009-07-27 10344
-
零输入响应与零状态响应分析2009-05-10 19856
-
线性系统的零输入、零状态及完全响应2008-09-24 11124
全部0条评论

快来发表一下你的评论吧 !

