

从绘图模式角度来识别应力结果显示中的“假象”
电子说
描述
众所周知,有限元分析中的应力计算是一个人们经常讨论的话题。本文结合前段时间一位名叫Marcus的网友(以下简称小M)发来的问题,从另一个工程师们常常忽略的方面——软件绘图显示设置的角度来谈谈应力结果的问题,希望能引起读者的思考和共鸣。
一、写在文前
实际上,有限元模型的应力解答分成很多种,以ANSYS软件为例,在Mechanical APDL和Mechanical(WB)中就包括积分点应力、单元节点应力、平均节点应力、仅表面平均的节点应力、跨体平均节点应力、不跨体平均节点应力等等。即便是基于同一个结果文件,绘制出来的应力分布图也会有所差异。
在很多情况下,不同软件之间比较计算结果也存在类似的问题。在比较有限元分析的应力结果时,也需要统一显示选项的标准。是不是感觉会有点绕 ?当然这里说的显示选项统一,并不总能保证可以发现结果在精度上是否存在问题,但也的确是软件使用者不能忽视的问题的另一个方面。下面来看具体的问题。
二、教你识别应力结果显示中的“假象”
小M最初发来的问题,只是两张在ANSYS Mechanical APDL中显示的应力分布图片,他发现在不同的显示模式下,应力等值线图中标注的最大应力值存在着明显的差异,那么到底哪个才是对的呢?
针对这个问题,我帮他进行了分析。在讨论问题的过程中,小M又陆续发来了一系列不同模型的计算结果的图片,这些进一步丰富了我们下面所要讨论的问题。
实际上,这个问题至少可以从显示模式、单元类型、网格密度等几个不同的方面来进行讨论。为了让读者能跟上我们的思路,还是大致按照小M的提问和我的回答过程来叙述这个问题。
1、线性四面体单元较粗网格划分的情况
小M最初发来的是两张如下所示的应力等值线图。
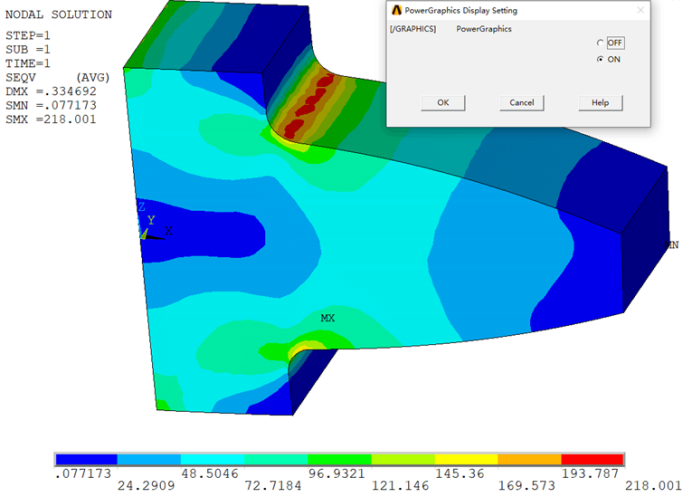
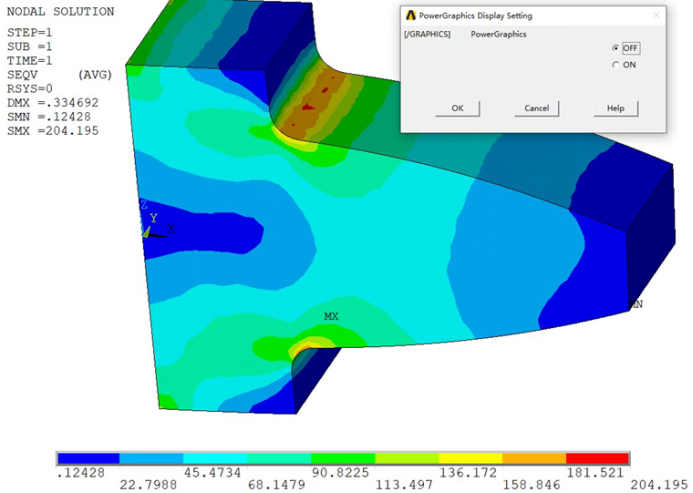
在这个问题中,涉及到Mechanical APDL中增强图形显示模式。可能现在使用Mechanical APDL的用户已经不多,更多的用户会选择使用ANSYS Workbench中的Mechanical进行结构计算。不过即使是Workbench用户,继续阅读本文下面的内容也会有所启发,因为相关问题的背景原理是相通的。
在这两张应力图中,增强显示模式的应力最大值大约为218,而非增强模式则约为204,差异还是很明显的。那么应以哪一个为准呢?我第一反应是这个问题的网格是不够精密的,所以就让小M发一下这次计算所采用的网格图。
如下图所示,这是他发来的网格图,这次计算是采用的线性的四面体单元。
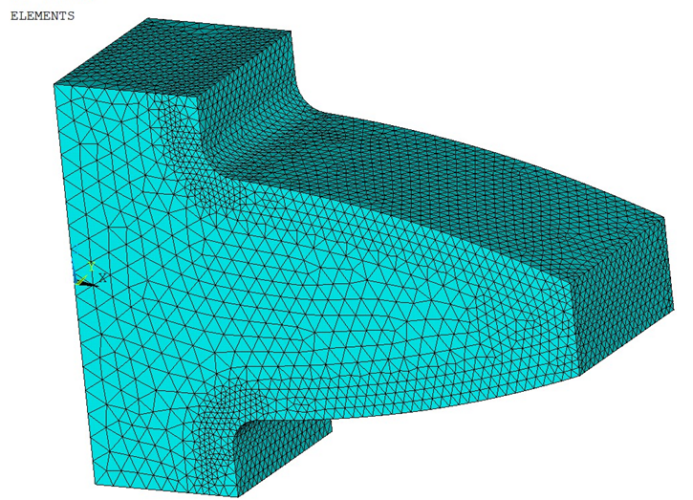
为了跟后面的计算结果相区别,我们姑且将这个模型称之为较粗的线性四面体网格模型。
我在看到这个网格后,建议小M加密网格再来算一次,一方面能够缩小两种显示模式下的应力值的差距,另一方面,也必然能够得到更精确的结果。
2、局部加密的线性四面体网格情况
小M也是很认真,加密到局部几乎是黑乎乎的程度,以至于不得不将视图局部放大,才能看到所关心部位在加密后的网格情况,如下图所示。

基于局部加密后的网格,分别得到增强显示模式以及非增强显示模式下的应力分布结果如下图所示。
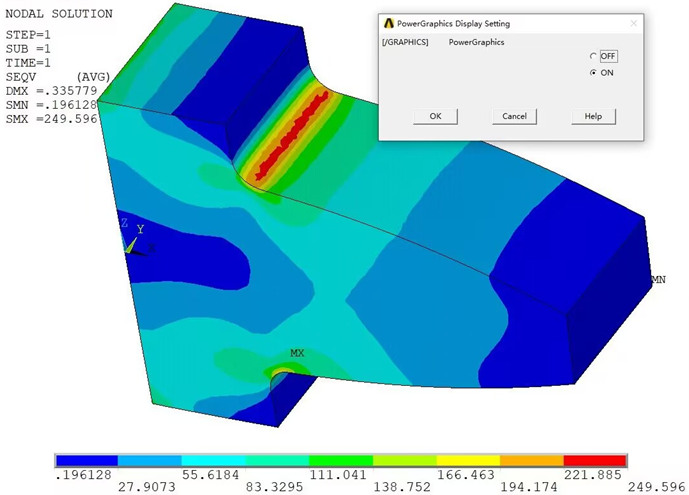
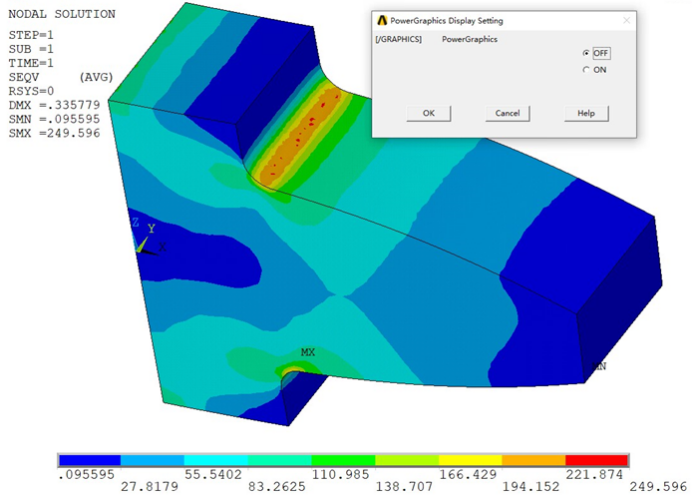
从上述显示的应力结果可知,是否采用增强显示模式,最大应力值已经几乎没有什么差异了。而且显示的应力最大值也与较粗网格的结果有了显著的不同,精度的话肯定提高了,但是显示云图上似乎毛毛刺还不是很“丝滑”,这个结果的精度到底怎么样呢?这可能还需要结合其他单元的计算结果进行横向的综合比较。由此可见,线性的四面体单元的确效率不高,因为网格的确已经很密了。
那么,能不能基于上述结果简单下结论,即:网格较粗时不同显示模式的应力数值就会有显著差异,而细致一些的网格就不会有差异呢?答案其实是否定的。目前只能说,线性四面体单元加密后的计算结果,对于显示模式变得不敏感了。
另一方面,四面体网格的应力结果在不同显示模式下的差异暴露出了计算精度(网格密度)方面存在的问题。但是,能不能反过来说不同显示模式下没有差异,就说明精度足够呢?答案同样是否定的。
What?网友小M感觉已经被我彻底绕晕了!可能很多读者读到这里时也都有着和小M一样的感受吧?
为了继续解答大家的疑问,我们接着往下看小M同学分析的六面体网格情况。
3、较粗的线性六面体网格划分情况
如下图所示为线性的六面体单元的网格,为了与后面的计算相区分,我们姑且称之为较粗的线性六面体单元网格。注意,这个模型并非全六面体网格,但至少在关心的区域是六面体的。
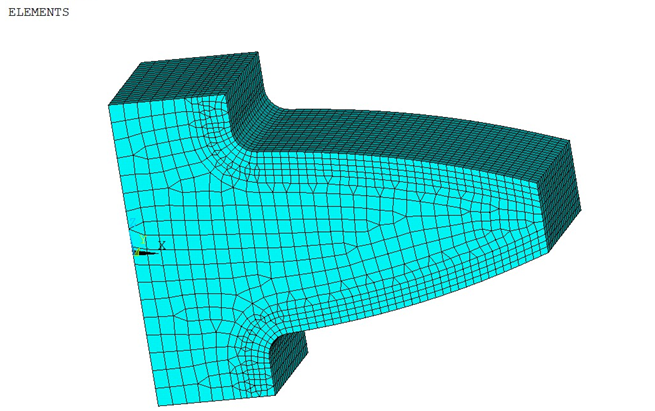
基于这一网格计算的应力解答,分别在增强显示模式和非增强显示模式下提取应力分布图,如下图所示。
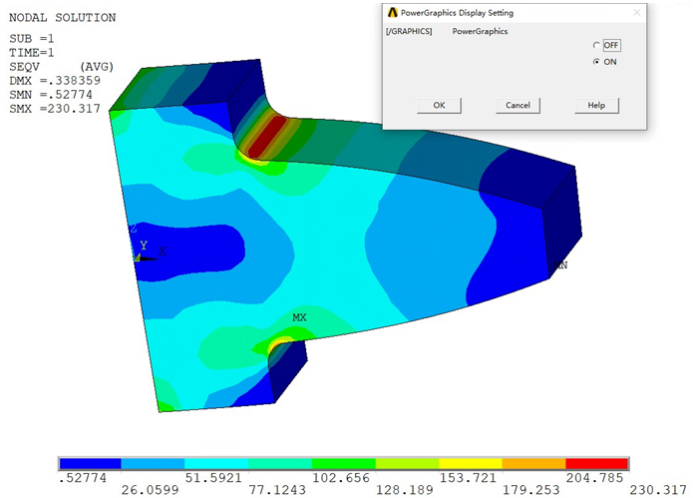
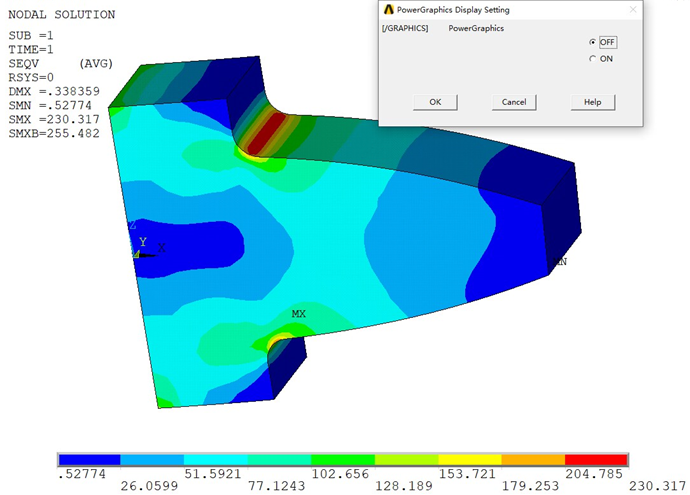
由上述计算结果可以发现,采用线性的六面体网格划分时,即使网格较粗,但是打开和关闭增强显示模式,等值线图显示的应力最大值却几乎没有差异。
但是另一方面,也注意到应力的数值和前面加密的线性四面体网格相比,却有着显著的差别。即便应力的分布较为“丝滑”,也不能够认定其是准确的。
小M认为,既然这个粗的六面体网格的结果在两种显示模式下都没有区别了,那么这个线性六面体单元加密后应该更加没有区别。饶是如此,他还是计算了下面的加密线性六面体网格的情况。
4、较细的线性六面体网格情况
小M继续发来了较细的线性六面体单元网格图,如下图所示。
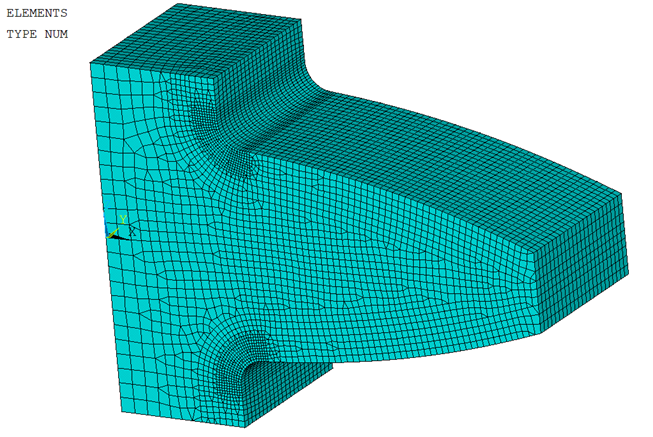
基于局部加密的线性六面体单元计算的应力结果,分别得到增强和非增强两种图形显示模式下的应力分布图如下。
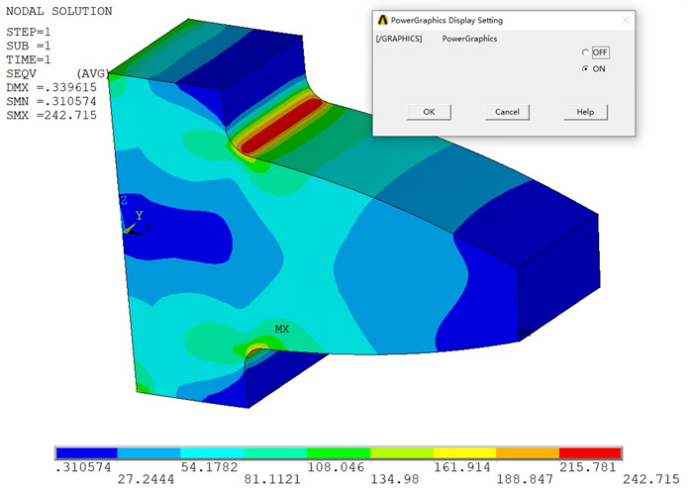
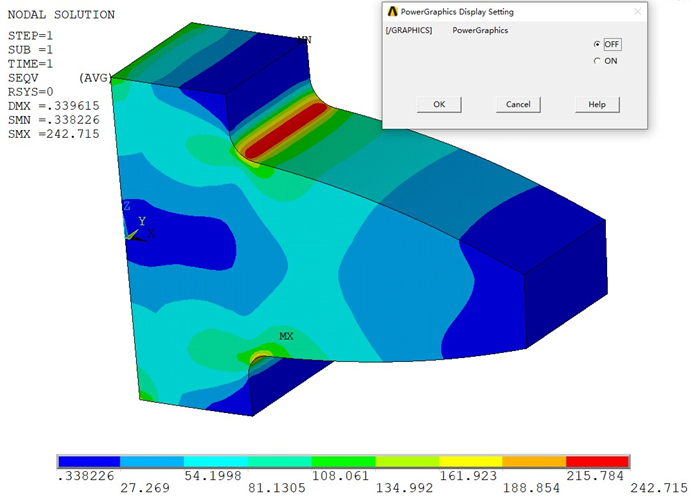
由上述计算结果可知,线性六面体单元在网格加密后的结果不出所料,对不同的显示模式依然不敏感。另一方面,从应力的最大数值上来看,倒是与加密的线性四面体网格的计算结果较为接近了。
5、较粗二次单元四面体网格情况
紧接着,小M又计算了二次单元的四面体网格情况,网格密度大致与前面线性四面体单元较粗的网格水平相当,如下图所示。
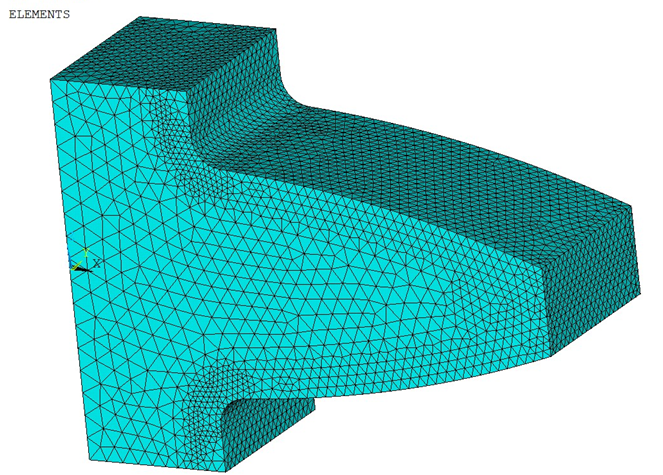
基于这个网格的应力计算结果,分别提取了打开或关闭增强显示模式下的应力等值线图,如下图所示。
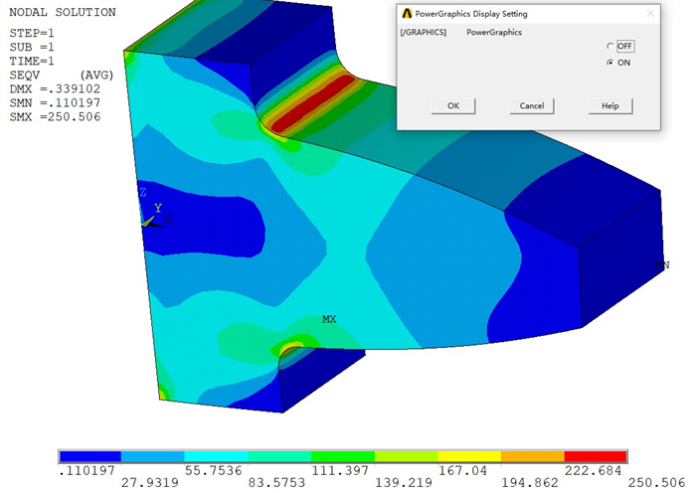
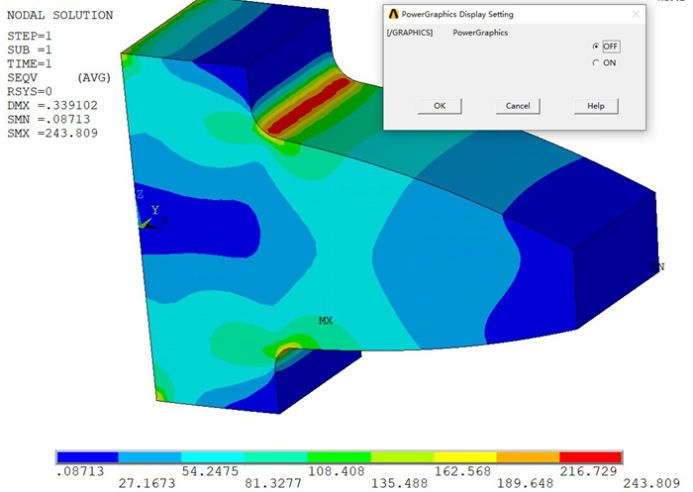
由上述结果可知,采用二次的四面体单元进行划分时,不同显示模式的结果还是有着比较明显的差异,但这种差异显然没有线性单元那么显著。另一方面,从应力的最大值角度来看,与前面加密网格的线性四面体单元、线性六面体单元的结果也都很接近了。
至此,很多人可能还想看看二次四面体网格加密情况的计算结果,实际上已经没有必要了。
三、结果汇总与讨论
为了对计算结果进行比较,首先把以上各种情况的结果汇总到下面的表格中,图中应力数值均精确到整数。
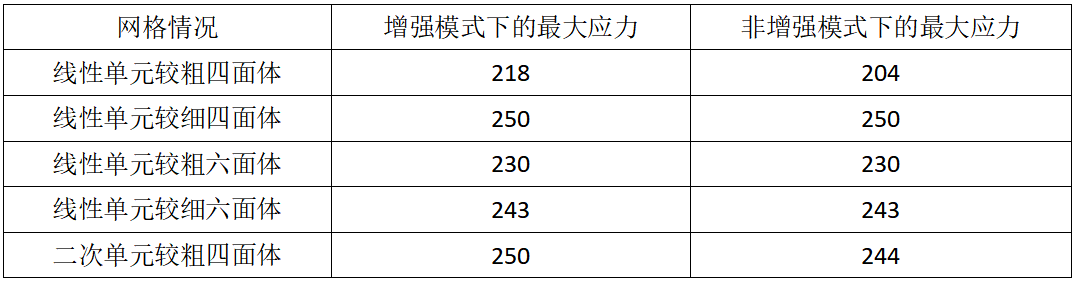
由上述表格中汇总的数据比较,结合ANSYS手册中关于增强显示模式的说明,可以得到如下几点认识或结论:
1、结论总结
(1)无论线性单元还是二次单元,当采用四面体划分时,是否选择增强模式显示,应力结果的最大值都存在显著的差异。之所以会有这样的差异,是由于增强显示模式在显示应力解时,只针对实体的外表面单元进行平均,而不考虑内部单元。如果四面体单元在外表面仅有一个节点而其余部分均处于体的内部时,显然是不参与计算的,因此四面体单元无论是线性还是二次,在两种模式下显示的应力结果会有显著差异。而且,由于打开增强模式时,由于参与平均的单元数少且表面应力值一般较大,因此其显示的数值一般更高,即偏于“保守”。这里对保守加了引号的原因,是因为这并不意味着偏于安全。
(2)是否打开增强模式下的应力数值差异会随着四面体网格的加密而变得不显著。尽管没有让小M再补充计算二次四面体单元网格加密后的情况,但结论也肯定是成立的。
(3)当采用六面体网格划分时,由于表面的节点仅属于表层单元,因此无论增强模式打开与否,因此显示的应力数值几乎没有差异。当然,加密后也同样没有差异。表格中尽管没有对二次六面体单元的情况进行计算,结论也肯定是成立的。在这里需要注意的是,线性六面体单元计算的情形,即使两种显示模式下的结果数值没有差异,且应力的等值线图也很“丝滑”了,也不能简单判定这个计算结果就是准确的。
2、讨论:到底哪一个应力结果是对的?
① 那么到底哪种情况下的应力结果是准确的呢?
是的,到目前为止还没有给出这个问题的答案,这是因为这个问题并不是本文所讨论的重点。实际上,应力的数值精确与否跟图形显示模式的选取之间没有实质性的关系,注意不是没有关系,而是没有实质性的关联。
② 哪个结果更准确,这其实是属于另一个问题。
前面的问题仅仅是在讨论不同的显示模式对结果数值显示的影响,而并不涉及哪个分析方案计算得出的精度更高。
③ 下面简单讨论一下上述问题计算结果的精度问题。
由于二次四面体单元的插值函数包含完备的二次项,因此它的计算结果精度要高一些。另外,线性单元加密后无论是四面体还是六面体,计算结果也比较接近了,且与二次四面体单元的计算结果的差异也仅在2%左右,这几个数值几乎已经是一致的了,因此可以认为这些解答都已经足够准确。
当然,与二次四面体单元的较粗网格相比,线性单元要达到相似精度,就需要进行网格加密。本问题中,小M实际采用的线性单元,其实是SOLID185的四面体退化形式以及六面体形式,这些线性单元的插值函数仅包含交叉乘积项而没有完备的二次项,因此只有使用相对较密的网格才能逼近问题的正确解答。
综上所述,应力计算是有限元分析中很重要的方面。抛开计算精度不讲,查看应力的数值时,还需要注意显示模式选择方面所带来的差异性。在不同的软件进行结果对比时,尤其要注意这类问题,在模式上不进行对标,仅查看和比较数值是没有意义的。
至此,小M终于彻底明白了,读者朋友们明白了吗?
[编者按]
本文中,作者对一个看似简单的问题进行了认真的剖析,针对网友小M的问题进行了深入浅出、由此及彼、由表及里的全面讲解。实际上,这也折射出作者在授课过程中一贯的技术风格——善于从实践中发现问题,并基于扎实的理论基础知识和对软件应用的深刻理解,在深入细致的分析后得到正确的认知。
审核编辑 :李倩
-
在NuEdu,pwm_dac示例程序中,让pwm来供电,为什么pwm产生的是输出假象的电压?2024-01-17 600
-
12864绘图+DS1302来显示时间2012-05-31 18849
-
从光源的角度来分析微型投影仪2012-11-05 2752
-
台式应力仪 PSV-2012013-03-20 2996
-
DFM分析之应力损伤2020-09-16 3674
-
从背光原理的角度分析LCD与LED的区别2020-10-30 1706
-
如何使用emWin的API显示面板上不同的绘图模式2023-08-23 456
-
M480使用emWin的API显示面板上不同的绘图模式2023-08-30 523
-
模糊模式识别在计算机识别中的应用研究2009-08-07 473
-
模式识别,模式识别是什么意思2010-03-06 2178
-
车载显示设备的显示角度调节2010-01-04 1870
-
从技术角度来深度剖析人脸识别技术2018-01-31 6678
-
从EMC设计的角度来解析无人机2018-08-04 6553
-
谷歌新增来帮助用户验证搜索结果显示的功能2021-02-03 2096
-
如何通过应力和应变管理实现高精度倾斜/角度检测性能2022-08-01 1136
全部0条评论

快来发表一下你的评论吧 !

