使用线性反馈移位寄存器生成伪随机数

线性反馈移位寄存器与完全描述它们的多项式一起引入。应用说明描述了如何实现它们以及可用于改善所生成数字的统计特性的技术。

介绍

LFSR（线性反馈移位寄存器）提供了一种在微控制器上快速生成非序列数字列表的简单方法。生成伪随机数只需要右移操作和 XOR 操作。图 1 显示了一个 5 位 LFSR。图 2 显示了 C 语言的 LFSR 实现，图 3 显示了 8051 汇编中的 16 位 LFSR 实现。

LFSR和多项式

LFSR 完全由其多项式指定。例如，6千-次多项式与每个项存在用方程 x 表示6+ x5+ x4+ x3+ x2+ x + 1。有 2 个(6 - 1)= 32 个这种大小的不同可能多项式。与数字一样，一些多项式是素数或原始数。我们对原始多项式感兴趣，因为它们会在移位时为我们提供最大长度周期。n 次的最大长度多项式将有 2n- 1个不同的州。每个班次后都会转换到新状态。因此，6千-次多项式将有 31 种不同的状态。1 到 31 之间的每个数字在重复之前都会出现在移位寄存器中。在基元 6 的情况下千-次多项式，只有六个。表 1 列出了所有基元 6千-次多项式及其各自的多项式掩码。多项式掩码是通过采用多项式的二进制表示并截断最右侧的位来创建的。掩码用于实现多项式的代码中。实现 n 的多项式掩码需要 n 位千-次多项式。

每个基元多项式都有奇数项，这意味着基元多项式的每个掩码都有一个偶数 1 位。每个原始多项式还定义了第二个原始多项式，即它的对偶。可以通过从每项的多项式次数中减去指数来找到对偶。例如，给定 6千-次多项式，x6+ x + 1，它的对偶是 x6-6+ x6-1+ x6-0，等于 x6+ x5+ 1.在表 1 中，多项式 1 和 2、3 和 4、5 和 6 是彼此的对偶。

表 2 列出了每个不同大小多项式的周期以及每个大小存在的基元多项式的数量。表 3 列出了每个不同大小的多项式的一个多项式掩码。它还显示了当 LFSR 初始化为 1 时，LFSR 在连续班次后将保持的前四个值。此表应有助于确保实现正确。

LFSR的结构

LFSR 的值永远不会为零，因为归零的 LFSR 的每个偏移都会将其保留为零。LFSR 必须初始化，即种子，为非零值。当 LFSR 保持 1 并移动一次时，其值将始终为多项式掩码的值。当寄存器除最高有效位外全部为零时，接下来的几个偏移将显示高位偏移到零填充的低位。例如，任何具有基元多项式的 8 位移位寄存器最终将生成序列 0x80、0x40、0x20、0x10、8、4、2、1，然后生成多项式掩码。

使用 LFSR 生成伪随机数

一般来说，基本的LFSR不会产生非常好的随机数。通过选择较大的LFSR并使用较低的位作为随机数，可以改进更好的数字序列。例如，如果您有一个 10 位 LFSR 并且想要一个 8 位数字，则可以将寄存器底部的 8 位作为您的号码。使用此方法，您将看到每个 8 位数字四次和零，三次，然后 LFSR 完成一个周期并重复。这解决了得到零的问题，但数字仍然没有表现出非常好的统计特性。相反，您可以将 LFSR 的子集用于随机数，以增加数字的排列并改善 LFSR 输出的随机属性。

在获得随机数之前多次移动LFSR也可以改善其统计特性。将LFSR移动其周期的一个因子将使总周期长度减少该因子。表2列出了各期间的因素。

LFSR 相对较短的周期可以通过将两个或多个不同大小的 LFSR 的值异或相处来解决。这些异或LFSR的新周期将是周期的LCM（最小公倍数）。例如，基元 4 位和基元 6 位 LFSR 的 LCM 是 LCM（15， 63），即 315。以这种方式加入 LFSR 时，请确保仅使用最小位数的 LFSR;使用少于此量是更好的做法。对于 4 位和 6 位 LFSR，不应使用超过底部的 4 位。在图 2 中，底部的 16 位用于 32 位和 31 位 LFSR。 请注意，对两个相同大小的 LFSR 进行异或运算不会增加周期。

LFSR的不可预测性可以通过用反馈项对一点“熵”进行异或来增加。这样做时应该小心——加上熵位，LFSR 到所有零的可能性很小。如果定期添加熵，LFSR 的归零将自行校正。这种与反馈项进行异或的方法就是CRC（循环冗余校验）的计算方式。

多项式不是生而相等的。有些多项式肯定会比其他多项式更好。表 2 列出了可用于最大 31 位大小的基元多项式的数量。尝试不同的多项式，直到找到满足您需求的多项式。表3中给出的掩模是随机选择的。

可以使用NIST的统计测试套件进行更广泛的测试。NIST还有几本出版物描述了随机数测试和对其他测试软件的引用。

图1.LFSR 的简化绘图。

图2.实现 LFSR 的 C 代码。

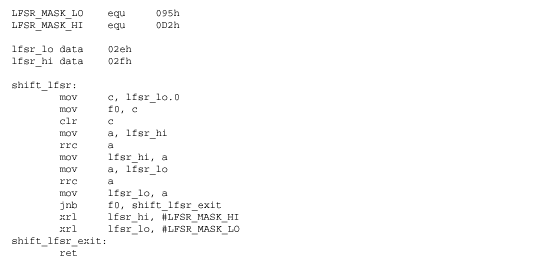
图3.8051汇编代码，用于实现掩码为0D295h的16位LFSR。

 

	不可约多项式	二进制形式	二进制掩码	面具
1	x6 + x + 1	1000011b	100001b	0x21
2	x6 + x5 + 1	1100001b	110000b	0x30
3	x6 + x5 + x2 + x + 1	1100111b	110011b	0x33
4	x6 + x5 + x4 + x + 1	1110011b	111001b	0x39
5	x6 + x5 + x3 + x2 + 1	1101101b	110110b	0x36
6	x6 + x4 + x3 + x + 1	1011011b	101101b	0x2D

度	时期	时期因素	不。这种次数的原始多项式
3	7	7	2
4	15	3, 5	2
5	31	31	6
6	63	3, 3, 7	6
7	127	127	18
8	255	3, 5, 17	16
9	511	7, 73	48
10	1,023	3, 11, 31	60
11	2,047	23, 89	176
12	4,095	3, 3, 5, 7, 13	144
13	8,191	8191	630
14	16,383	3, 43, 127	756
15	32,767	7, 31, 151	1,800
16	65,535	3, 5, 17, 257	2,048
17	131,071	131071	7,710
18	262,143	3, 3, 3, 7, 19, 73	7,776
19	524,287	524287	27,594
20	1,048,575	3, 5, 5, 11, 31, 41	24,000
21	2,097,151	7, 7, 127, 337	84,672
22	4,194,303	3, 23, 89, 683	120,032
23	8,388,607	47, 178481	356,960
24	16,777,215	3, 3, 5, 7, 13, 17, 241	276,480
25	33,554,431	31, 601, 1801	1,296,000
26	67,108,863	3, 2731, 8191	1,719,900
27	134,217,727	7, 73, 262657	4,202,496
28	268,435,455	3, 5 29, 43, 113, 127	4,741,632
29	536,870,911	233, 1103, 2089	18,407,808
30	1,073,741,823	3, 3, 7, 11, 31, 151, 331	17,820,000
31	2,147,483,647	2147483647	69,273,666
32	4,294,967,29	3, 5, 17, 257, 65537	不可用

度	典型面罩	连续班次后LFSR中的前四个值
3	0x5	0x5	0x7	0x6	0x3
4	0x9	0x9	0xD	0xF	0xE
5	0x1D	0x1D	0x13	0x14	0xA
6	0x36	0x36	0x1B	0x3B	0x2B
7	0x69	0x69	0x5D	0x47	0x4A
8	0xA6	0xA6	0x53	0x8F	0xE1
9	0x17C	0x17C	0xBE	0x5F	0x153
10	0x32D	0x32D	0x2BB	0x270	0x138
11	0x4F2	0x4F2	0x279	0x5CE	0x2E7
12	0xD34	0xD34	0x69A	0x34D	0xC92
13	0x1349	0x1349	0x1AED	0x1E3F	0x1C56
14	0x2532	0x2532	0x1299	0x2C7E	0x163F
15	0x6699	0x6699	0x55D5	0x4C73	0x40A0
16	0xD295	0xD295	0xBBDF	0x8F7A	0x47BD
17	0x12933	0x12933	0x1BDAA	0xDED5	0x14659
18	0x2C93E	0x2C93E	0x1649F	0x27B71	0x3F486
19	0x593CA	0x593CA	0x2C9E5	0x4F738	0x27B9C
20	0xAFF95	0xAFF95	0xF805F	0xD3FBA	0x69FDD
21	0x12B6BC	0x12B6BC	0x95B5E	0x4ADAF	0x10E06B
22	0x2E652E	0x2E652E	0x173297	0x25FC65	0x3C9B1C
23	0x5373D6	0x5373D6	0x29B9EB	0x47AF23	0x70A447
24	0x9CCDAE	0x9CCDAE	0x4E66D7	0xBBFEC5	0xC132CC
25	0x12BA74D	0x12BA74D	0x1BE74EB	0x1F49D38	0xFA4E9C
26	0x36CD5A7	0x36CD5A7	0x2DABF74	0x16D5FBA	0xB6AFDD
27	0x4E5D793	0x4E5D793	0x6973C5A	0x34B9E2D	0x5401885
28	0xF5CDE95	0xF5CDE95	0x8F2B1DF	0xB25867A	0x592C33D
29	0x1A4E6FF2	0x1A4E6FF2	0xD2737F9	0x1CDDF40E	0xE6EFA07
30	0x29D1E9EB	0x29D1E9EB	0x3D391D1E	0x1E9C8E8F	0x269FAEAC
31	0x7A5BC2E3	0x7A5BC2E3	0x47762392	0x23BB11C9	0x6B864A07
32	0xB4BCD35C	0xB4BCD35C	0x5A5E69AE	0x2D2F34D7	0xA22B4937

 

审核编辑：郭婷