电容的串并联、充放电电路

电容的串并联

1 并联

将两个或多个电容器同极性的电极连接在一起，接入电路的连接方式为电容器的并联，两个电容器的并联如图所示。

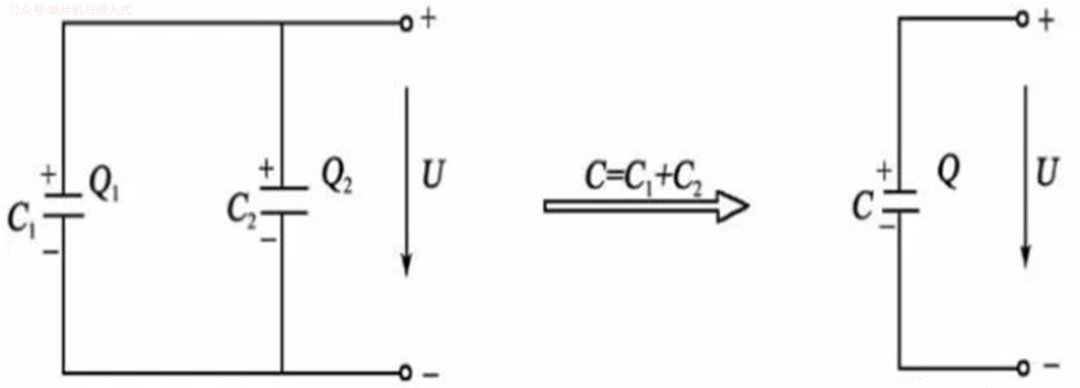
电容并联总电容等于个并联电容之和。

电容器并联，相当于增大电容器极板的正对面积，所以等效电容总是大于其中任何一个电容器的电容。

2 串联

将下一个电容器的正极性端与上一个电容器的负极性端连接，以第一个电容器的正极性端和最后一个电容器的负极性端与电路连接，这样的连接方式称做串联。两个电容器串联如下图所示。

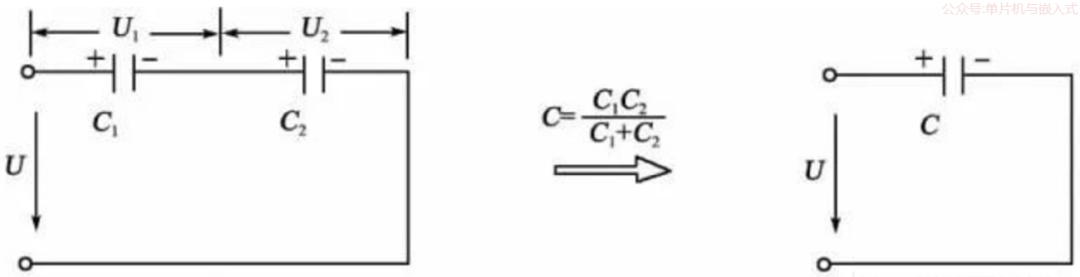
电容器串联时，等效电容的倒数为各电容的倒数之和。

电容器串联后，相当于增大电容器极板之间的距离，等效电容比任何一个电容器的电容都小。电容器串联，可以分担电路的电压。

电容的充放电

1 电容充电

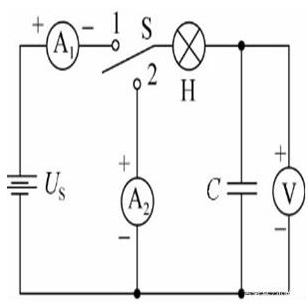
在下图所示的电路中，US为恒压源，C为电容量很大的电容器，S是单刀双掷开关，H是灯泡。先把开关S与接点1闭合，电源对电容器充电。

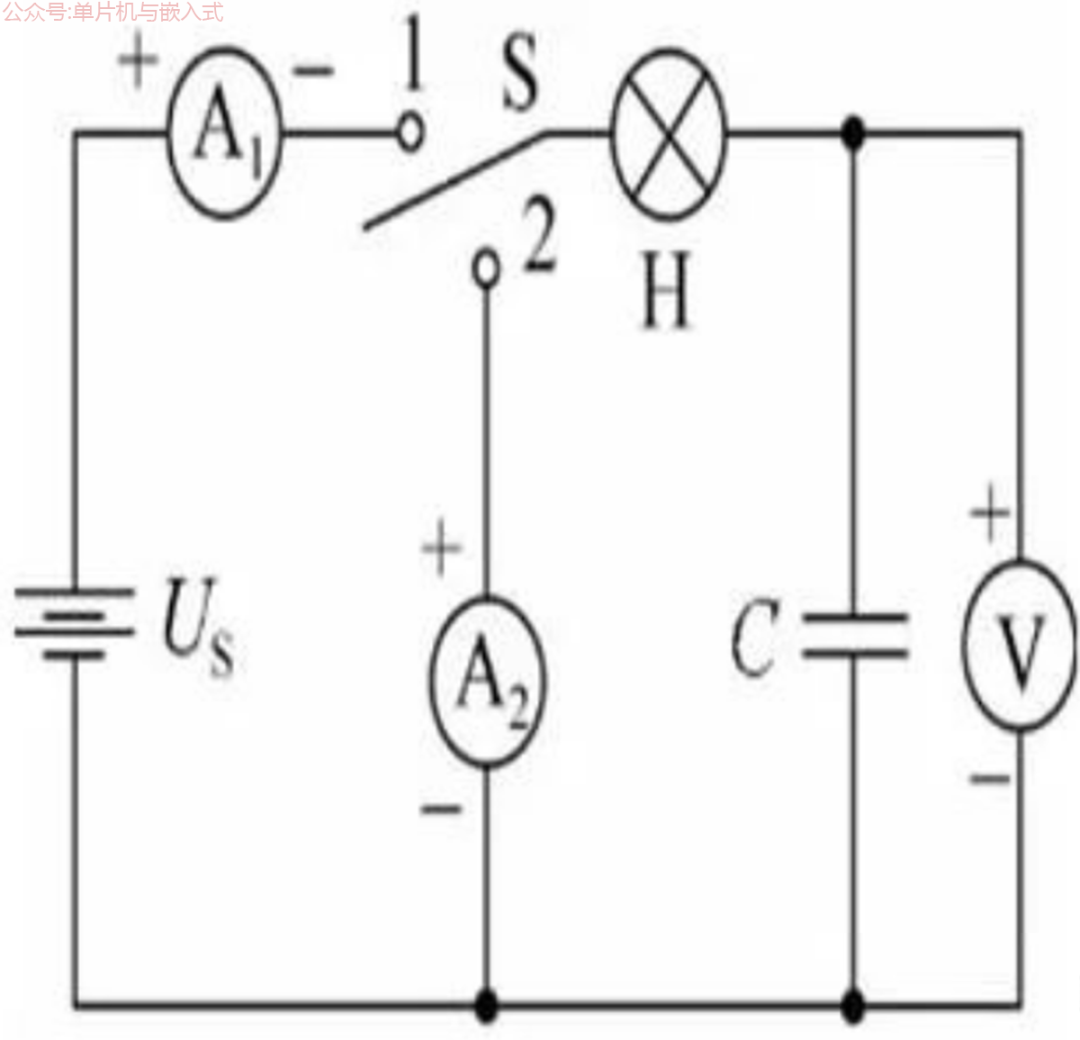
在充电过程中并没有电荷直接通过电容器内部的电介质，而是电子由电容器的正极板→灯泡→电流表→电源正极→电源负极→电容器负极板作定向移动，形成电流的，如下图所示。

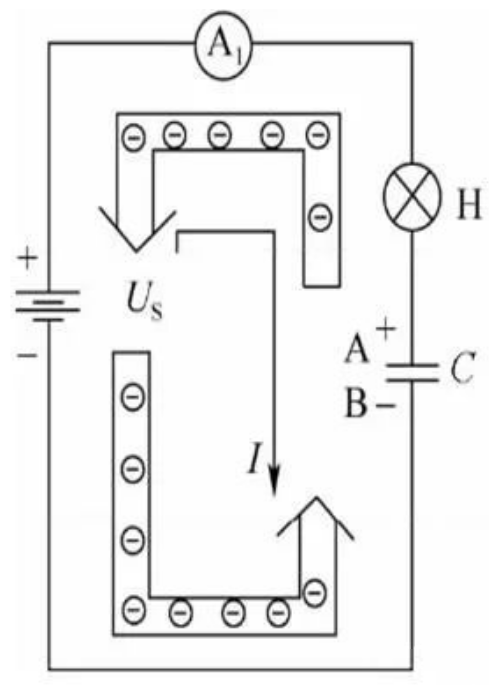
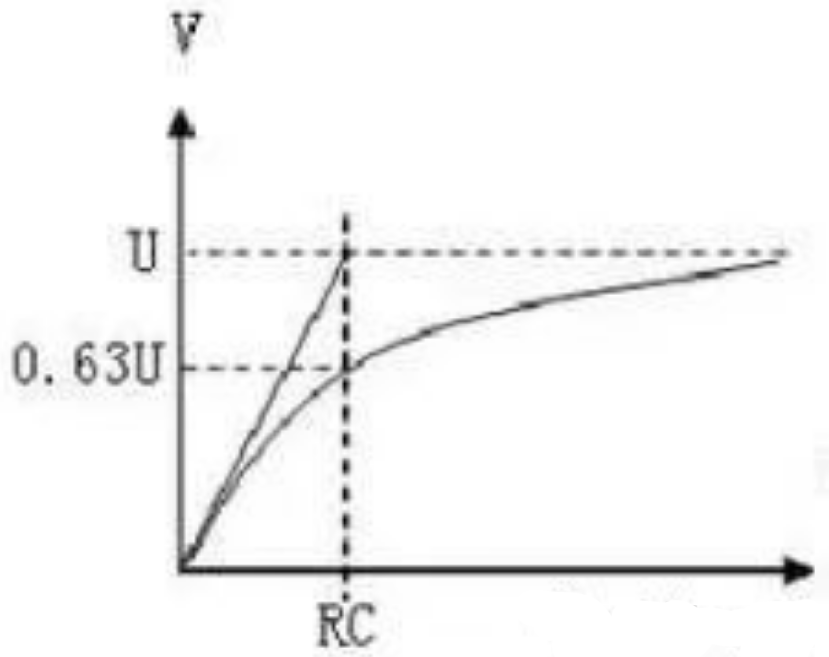
充电过程为充电的开始阶段，充电电流较大，u上升较快，随着的增长，充电电流逐渐减小，且u的上升速度变缓，而向着电源电压E趋近。曲线如下图所示。

在电路上可以观察到灯会由亮到暗，最后熄灭。涉及到的相关公式如下：

充电时间常数：

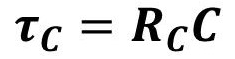
充电电压：

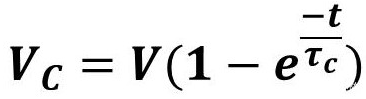
充电电流：

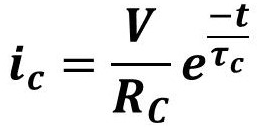
时间常数与充电电压关系如下：

τc--------充电电压Vc(v)

0----------0%

1τc------63.2%

2τc------86.5%

3τc------95%

4τc------98.2%

5τc------100%

2 电容放电

把开关S与接点2闭合，电容对灯H放电。

由图可知，电容器在放电过程中，也没有电荷通过电容器内部电介质。

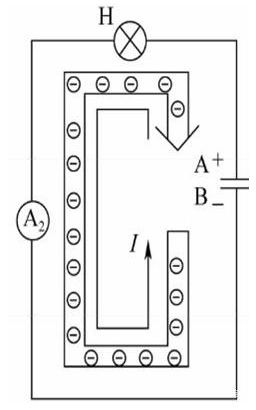
电容的放电过程为刚开始时，电流最大，之后逐渐减小;电容器带电量在放电过程开始时最大，之后也逐渐减少，当带电量减小为零时，放电完毕，电流减小为零。

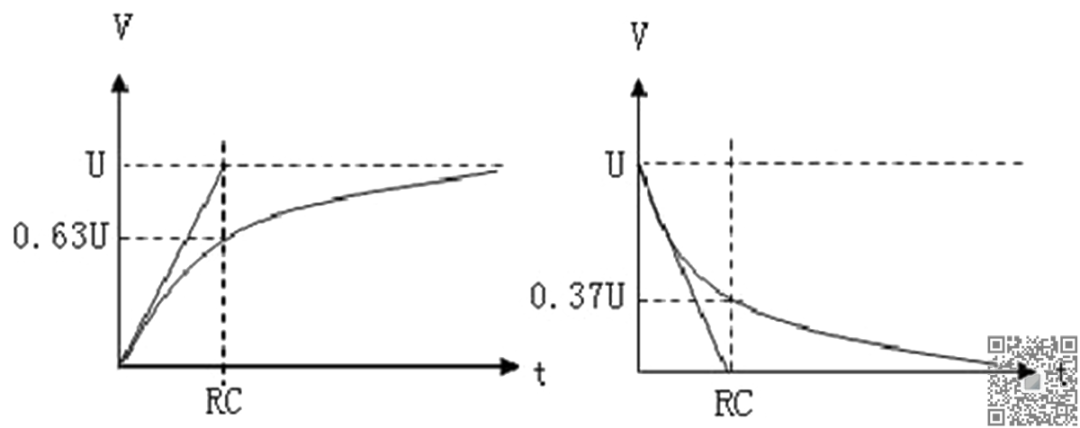
如上图，对于在高频工作下的RC电路，由于寄生参数的影响，很难根据电路中各元器件的标称值来计算出时间常数RC，这时，我们可以根据电容的充放电特性来通过曲线方法计算，前面已经介绍过了，电容充电时，经过一个时间常数RC时，电容上的电压等于充电电源电压的0.63倍，放电时，经过一个时间常数RC时，电容上的电压下降到电源电压的0.37倍。

在电路上可以观察到灯会由亮到暗，最后熄灭。这个现象在生活着常见到，比如有些电子设备你关电源后，设备上的电源指示灯慢慢熄灭就是电容放电现象。有很多电源插板上能看见。

电容放电涉及到的相关公式如下：

电容放电时间常数：

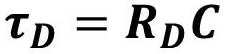
电容放电电压：

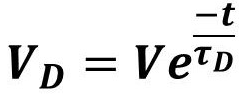
电容放电电流：

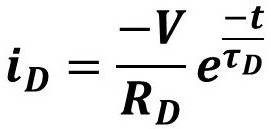
总结

当我们想要的电容值，手上没有时，就可以通过电容的串并联得到。通过电容的充放电就可以得到电容的一个特性，电容两端电压不能发生突变。电容的充电过程记不清没有关系，但是时间常数与充电电压的关系要记住以及电压不能发生突变这个特性也要记住，这两点在你设计和分析电路上会提供很大的帮助。

审核编辑：汤梓红