关于FPGA 脉动阵列的设计方案解析

一：定义

脉动阵列：数据流同步流过相邻的二维阵列单元的处理器结构，一般不同方向流过不同数据。如下图：

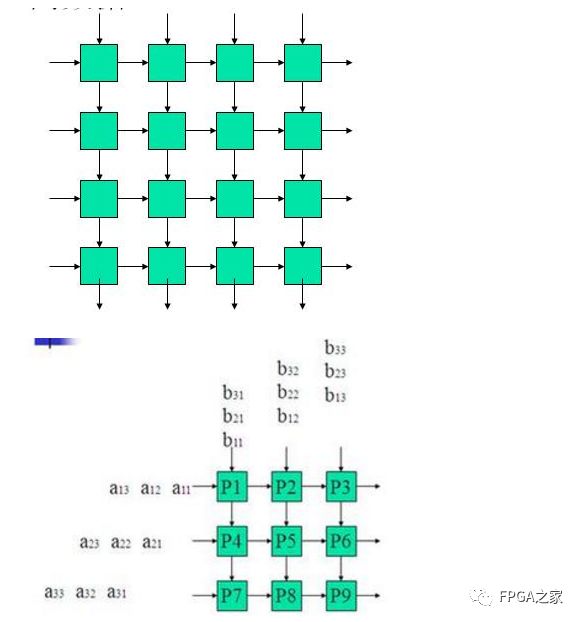
二维不同数据在同一时钟下依次输入每个处理单元，而后完成乘法并存在其寄存器中。

二：举例

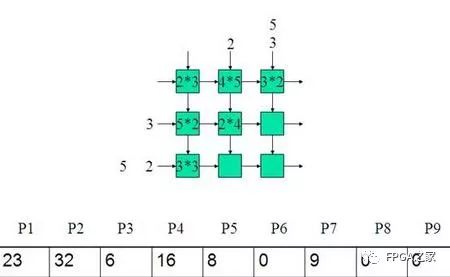
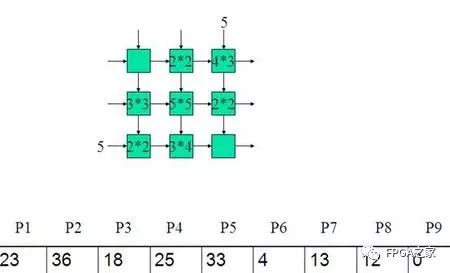
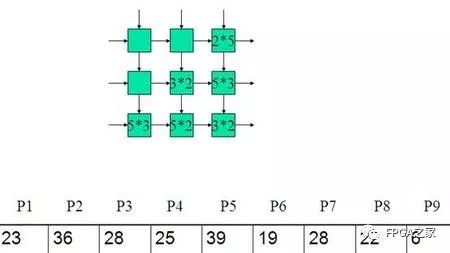
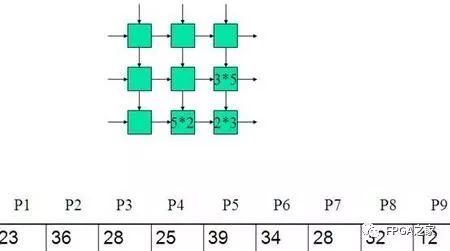
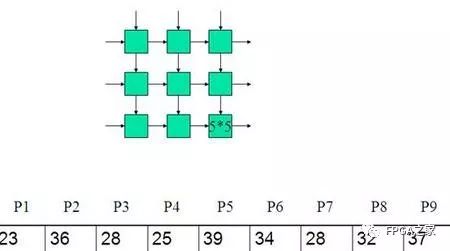
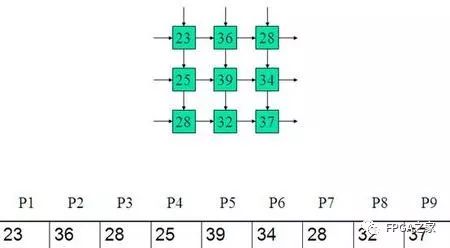
三：设计

结构：

单个PE的代码

module pe(clk, reset, coeff, in_x, in_y, out_x, out_y);

parameter size = 8;

input clk, reset;

input [size-1:0] in_x, coeff;

input [size+size-1:0] in_y;

output [size-1:0] out_x;

output [size+size-1:0] out_y;

reg [size+size-1:0] out_y;

reg [size-1:0] out_x;

always@(posedge clk)

begin

 if(reset) begin

 out_x <= 0;

 out_y <= 0;

 end

 else begin

 out_y <= in_y + (in_x * coeff);

 out_x <= in_x;

 end

end

endmodule

 

四个PE，其余类推

//***** main ****************************

module systolic(clk, reset, input_x, output_y);

parameter size = 8;

input clk, reset;

input [size-1:0] input_x;

output [size+size-1:0] output_y;

wire [size-1:0] pe0_x, pe1_x, pe2_x, pe3_x;

wire [size+size-1:0] pe1_y, pe2_y, pe3_y;

wire [size-1:0] h0 = 8'h01;

wire [size-1:0] h1 = 8'h01;

wire [size-1:0] h2 = 8'h01;

wire [size-1:0] h3 = 8'h01;

wire [size+size-1:0] pe4_y = 16'h0000;

pe pe_0(clk, reset, h0, input_x, pe1_y, pe0_x, output_y);

pe pe_1(clk, reset, h1, pe0_x, pe2_y, pe1_x, pe1_y);

pe pe_2(clk, reset, h2, pe1_x, pe3_y, pe2_x, pe2_y);

pe pe_3(clk, reset, h3, pe2_x, pe4_y, pe3_x, pe3_y);

endmodule

=========================================================================================================

脉动阵列（Systolic Array）计算矩阵乘法（Array Multiplication）

下一个目标是实现流水线输出，提升硬件资源的利用率。

脉动阵列(Systolic Array)：数据流同步流过相邻的二维阵列单元的处理器结构，一般不同方向流过不同数据。

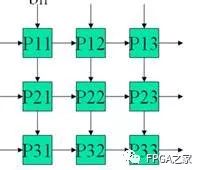
结构：

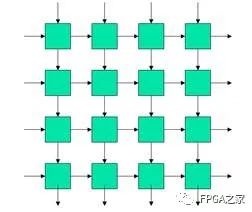
矩阵计算：

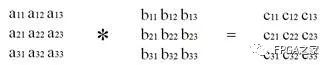
C语言描述每个输出矩阵中的值：

For I = 1 to N

 For J = 1 to N

 For K = 1 to N

 C[I,J] = C[I,J] + A[J,K] * B[K,J];

运用N x N processing units，输入数据呈批次输入：

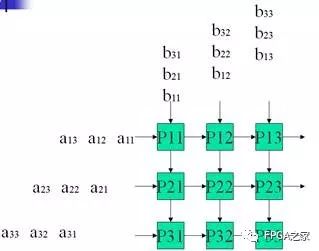
二维不同数据在同一时钟下依次输入每个处理单元，而后完成乘法并存在其寄存器中。

其中每个PE（处理单元）结构如下：

是一个乘加单元 c=c+(a*b)

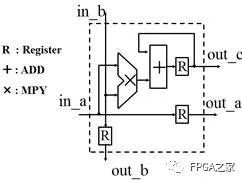
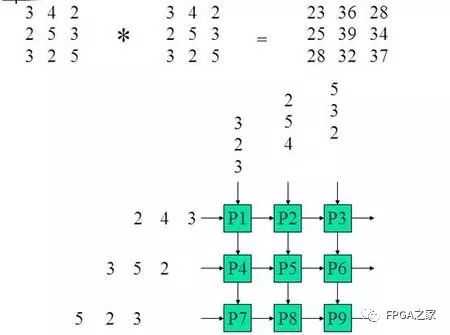
例子：计算两个３×３矩阵的乘积

结构：

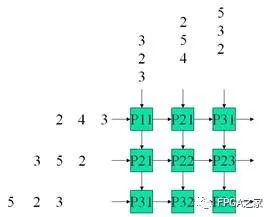
在CLK驱动下的每一个步骤如下:

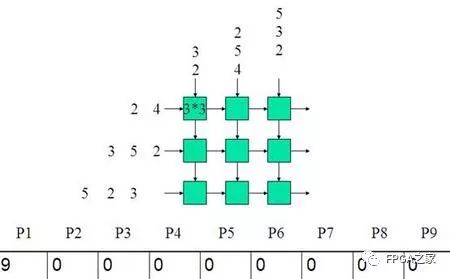
Clk1:

 

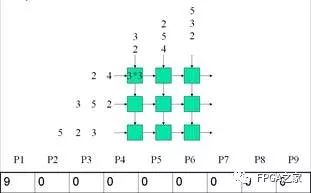
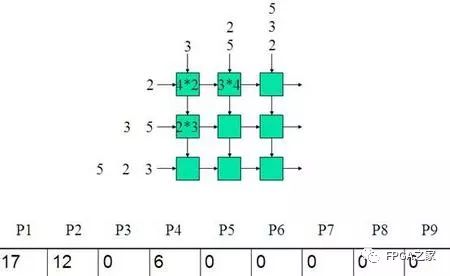
Clk2:

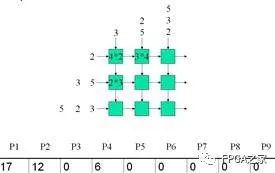
Clk3:

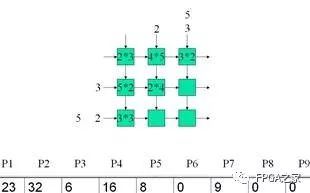
Clk4:

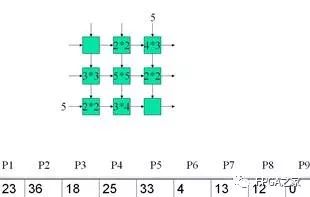
Clk5:

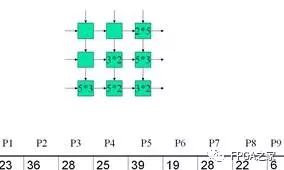
Clk6:

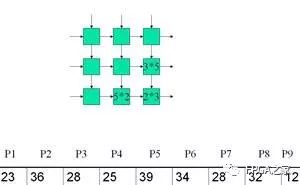
Clk7:

Clk8:输出

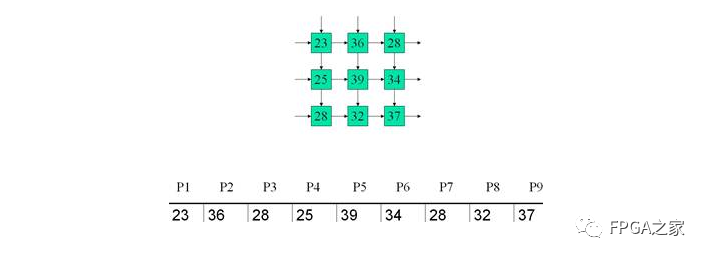
功能仿真图：

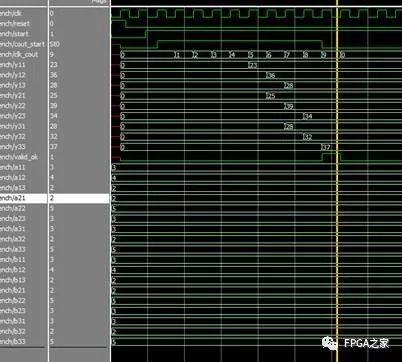
在start 上升沿到来后的第一个CLK上升沿开始计数

Count_start高电平期间

Cout=1时，准备a11和b11;

Cout=2时，将数据打入寄存器，并计数出a11*b11;

Cout=3时，计数a11*b11+a12*b21

Cout=4时，计数a11*b11+a12*b21+a13*b31

Cout=5时，用寄存器打一拍输出Y11。

其他类似。

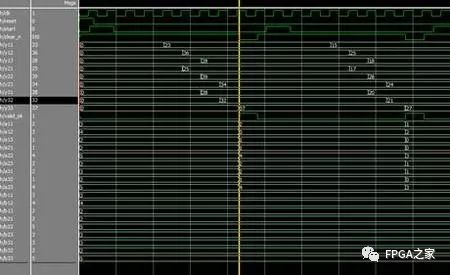
时序仿真图：

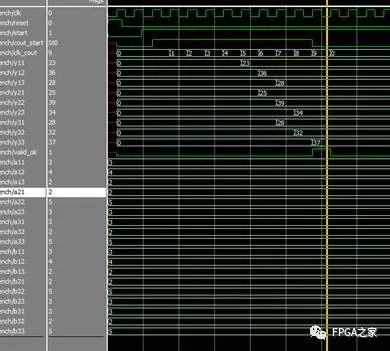
连续运算，中间忘了将乘加单元寄存器清零的情况，功能仿真：

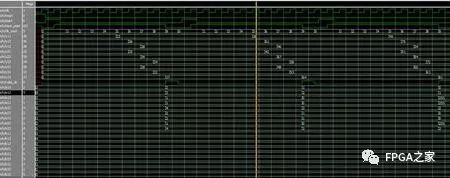
每次计算出结果后清零寄存器，修改后的功能仿真图：

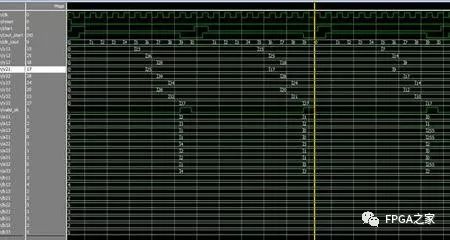
数据在送入运算单元之前，采用寄存器打一拍，功能仿真图：

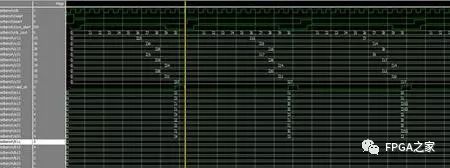
状态机便于实现控制。

状态机控制：功能仿真

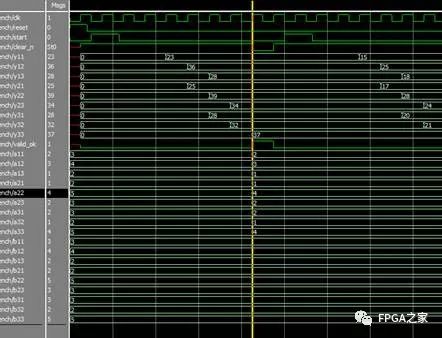
时序仿真图：

二维流水线结构矩阵乘法（Array Multiplication）

上一篇文中建立了矩阵乘法运算的数据路径，从仿真结构中可以看出整个计算方案的可行性，但是存在一个问题，就是硬件运算单元的资源利用率不高。这是什么意思呢？就是说，在每次计算两个3*3矩阵的乘法之前，需要将整个运算单元中的每个寄存器都清零，但是9个输出结果不是在同一个时刻输出，有先有后。当最先出结果的P11计算出第一个结果之后，它就不再输出新值了。其实这时硬件电路是存在的，而且是在不断计算出新值，只是这些值不是我们需要的有效值。那么如果将这些硬件资源完全被利用起来，让它们在最短的时间间隔里都有有效正确数据输出呢。

其实要说的就是流水线设计思想，我们只需要当P11单元计算出新的值，下个CLK将其计算结果输出（只要有另一个机制接收这些值），然后将其清零（如果不清零，那个会累加了上次的计算结果），再然后就可以将下个要计算的两个3*3矩阵对应位置上面的新值输入给P11单元，让其计算两个数的乘积。

其他单元类似，思想就是在输出结果后立即做清零和赋新值，不必等整个计算单元都出结果之后才开始进行下个矩阵乘法的计算。

那么从大局来看，就出现个这样的情况：在上个矩阵计算还没有完全计算出9个值的时候（右下角部分还在计算），左上角的单元就已经开始下个矩阵乘法的计算。关于输出就是，每个CLK都有有效的数据输出，产生了流水输出。而这些输出是从这整个二维矩阵计算单元的某些地方同时输出的，就像水流即向下流也向右流，只是在这里水流对应了数据输出。

回顾一下这样做的目的是什么：为了增加整个运算单元的利用率。做了改进，我们可以看出，每个CLK到来时，每个计算单元中的乘法和加法器的运算都是有效的计算。我们一定要记住FPGA做运算和CPU做计算的不同点。FPGA做运算，那些设计好的运算单元，不管你对这些运算单元操作或者不操作，它们都已经以硬件电路的形式存在了，也就是说，每个CLK到来时，它们都进行了一次计算。那么如何有效的利用这些运算单元，就是不要让它们做无效的计算，让它们每一次的计算都对我们来说是有效的，是一个对整个单元输出有影响的计算。而想实现这样的功能流水线设计方法是必须要采用的。只是有时候单向流水（一维）更容易被我们所理解。其实这二维运算单元也是如此，也可以产生流水。

相对于不采用流水线操作，数据路径不必做太多修改，主要是控制单元更为复杂，要考虑何时对某个单元清零，何时再对其赋值，何时把数据读走等。这些需要比较精准的调度。有人会想，那么这样是不是需要更多状态机状态？答案是肯定的。那么是不是需要更多的硬件资源的开销呢？答案也是肯定的。那么这种流水线的优势在哪呢？其实是速度上面的优势，有时候在不能提高整个系统的工作频率的情况下，再消耗一点资源来提高其它部分（运算单元）的利用率也是一个很好的提高运算速度的办法。（注：这并不等同于面积与速度的法则）其实这也是一个比较好的，硬件算法优化方案。我们可以将其归纳为以优化算法路径的算法优化方法。

下面是仿真结果：

 

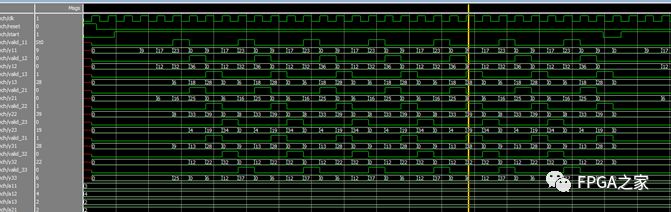
矩阵还是之前的矩阵。可以看出每个CLK都有2-3个有效输出。

增加了Valid信号，当其为高电平时，说明对应运算单元输出是有效值。其实在算法成熟之后，这些Valid信号是可以撤销的，因为我们完全知道了，输出的规律，只需要在特定的时间读走数据即可。而且我们可以将这些数据合并到几根连续有效的总线上面。让每个总线上面每个CLK都是有效值。（笔者将按照此方法，继续优化输出总线）

下面是对输入最大值时的输出仿真，主要是看数据会不会益处：

测试8bits输入最大值255对应的输出值：

时序仿真：

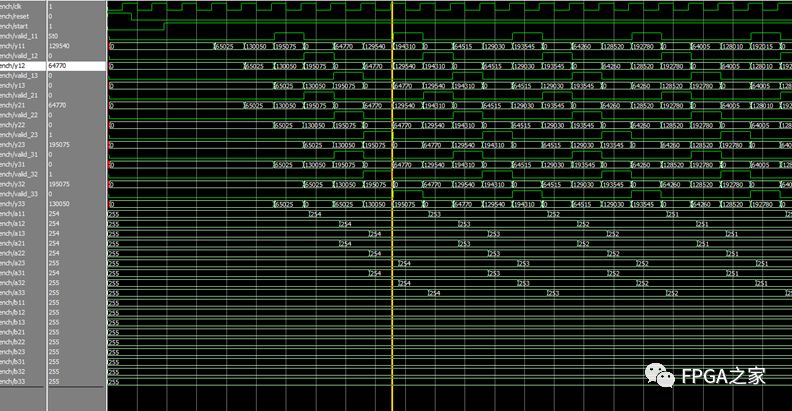
255*255+255*255+255*255=195075

255*254+255*254+255*254=194310

编辑：黄飞