中频压控振荡器所需的设计基础和挑战

本应用笔记探讨了实现无微调、固定频率、中频压控振荡器（VCO）所需的设计基础，并指出了保证电路正常工作的挑战。VCO 是大多数无线系统架构中必不可少的组件。在双变频方法中，需要固定频率的中频VCO来控制从中频到基带和/或基带到中频的频率转换。

本文由两部分组成，第1部分探讨了实现无微调、固定频率、中频压控振荡器（VCO）所需的设计基础，并指出了保证电路正常工作的挑战。VCO 是大多数无线系统架构中必不可少的组件。在双变频方法中，需要固定频率的中频VCO来控制从中频到基带和/或基带到中频的频率转换。

双转换系统需要两个振荡器。通常，第一个（RF VCO）在整个输入通道频率范围内调谐，第二个（IF VCO）以频率规划建立的单个频率工作。RF VCO可用作模块、IC或分立元件电路，模块和IC更为常见。对于中频VCO来说，市场上几乎没有小型、高性价比的模块。可能的原因包括需要许多任意的IF频率，以及需要大值电感器，这些电感器在生产中无法进行激光调整（调整）。因此，IF VCO通常作为分立电路或IC的一部分实现。

Maxim率先推出了一款新型VCO IC，用于其他板级RF/IFIC缺乏该功能的无线系统。本文的第2部分将介绍该IC，讨论其开发，并详细介绍其实现的简单且经济高效的应用。

分立元件VCO提供足够的自由度，以满足大多数系统的性能目标（调谐范围、输出功率、相位噪声、电流消耗、成本等）。然而，对于产量更大、成本敏感的现代产品，生产线调整振荡频率是不可接受的。因此，RF工程师不得不设计一种在组装过程中不需要调整的VCO，即无微调VCO。设计不是微不足道的。除了了解VCO设计基本原理外，还需要大量的RF工程工作，以确保设计正确居中，并且振荡器在元件值、温度和电源电压的所有允许变化中调谐到所需频率。以下讨论在解释无修整中频VCO设计中的相关问题时，试图培养对任务重要性的认识。

VCO 拓扑

虽然几种振荡器拓扑可用于构建实用的RF VCO，但Colpitts共集电极拓扑已被证明在许多商用VCO模块和无数分立VCO电路中取得成功（图1）。这种拓扑结构适用于从IF到RF的宽工作频率范围。

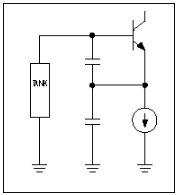
图1.基本的科尔皮茨振荡器。

灵活、低成本和合理的高性能VCO可以采用由低成本表面贴装电感器和变容二极管组成的电感电容（LC）谐振电路构成。振荡器谐振电路是控制振荡频率的并联谐振电路;电感或电容器的任何变化都会改变振荡频率。电感和变容二极管可以将可变谐振实现为并联或串联模式网络。

并行模式网络可用于较低频率，其中大值变容二极管不切实际，电感值可以做得更大。并行模式配置还允许对振荡器进行直接分析。在本文的其余部分，无需微调的中频VCO将使用Colpitts风格的振荡器，使用并联模式LC谐振（图2）。

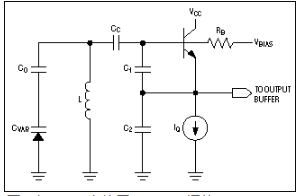
图2.在 VCO 中使用 Colpitts 拓扑。

Colpitts振荡器在几本教科书中进行了讨论，并且已经推导出各种方程来预测振荡器的行为，特别是Colpitts拓扑。振荡器通过电路的反馈放大器模型进行推广。确切振荡频率的表达式可以通过在该模型中等同阻抗来得出，但这些表达式很麻烦，并且无法深入了解设计过程。

或者，可以以更简单但不太准确的方式分析Colpitts振荡器，从而提供一组更清晰，更有洞察力且对一阶振荡器设计有用的设计方程。首先，可以将Colpitts振荡器重新绘制为具有正反馈的LC放大器（图3）。此视图可用于计算环路增益、振荡幅度和相位噪声。为了预测启动行为和振荡频率，还可以将原始电路重新绘制为负阻抗加谐振器结构（图 4）。来自这两个视图的方程被组合为一组用于Colpitts振荡器的控制方程（Meyer 1998）。

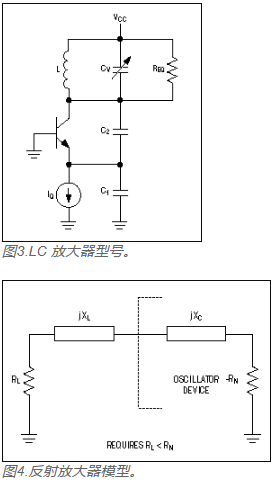
科尔皮茨振荡器的基本设计公式

忽略寄生元素，此分析的基本方程假设CC> C1和 C2和 C1> C π（Cπ 是基极-发射极电容）。计算振荡频率（fO） 如下：

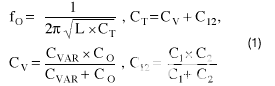
计算谐振电路的品质因数（QT） 如下：

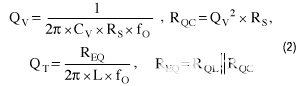
估计振荡幅度如下：

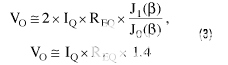
按如下方式计算环路增益和启动标准：

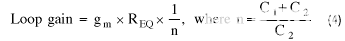
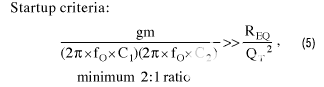
计算失调频率 （f ） 下的科尔皮茨振荡器相位噪声 （PN）m） 从承运人处，如下所示：

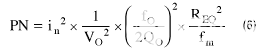
无微调VCO方法

开发无修剪VCO在概念上相对简单。如果振荡器具有足够的额外调谐范围来克服产生频率偏移的所有误差源（例如，元件容差），则可以消除振荡器频率调整。乍一看，它似乎足够直观和简单，只是为了提供大量的振荡器调谐范围并调出所有误差源。然而，对于给定的调谐电压范围，有限的可变电容对频率调谐范围施加了基本限制，并且VCO的电气性能要求通常会在达到该限制之前限制调谐范围。

不幸的是，调谐范围过大的振荡器会带来一些负面影响。非常宽的范围需要变容二极管与谐振二极管的重电容耦合，这大大降低了谐振二极管电路的Q值。其结果是相位噪声更大（谐振幅与晶体管噪声相比减小），对调谐线噪声的灵敏度更高（直接转化为频率调制），变容二极管两端电压摆幅过大的可能性，潜在的启动问题，以及设计环路滤波器的更大挑战。这些因素导致的结论是，过度的调谐范围是不可取的。实际上，它不应大于吸收所有错误源所需的最小值。

 

词汇表

CO= 变容二极管耦合电容

CT= 总电箱电容

C增值= 变容二极管电容

fm= PN 的偏移频率（以 Hz 为单位）

fO= 振荡频率

gm= 双极晶体管（振荡器）跨导

我n= 收集器散粒噪声

我Q= 振荡器晶体管偏置电流

QL= 电感 Q

QT= 油箱 Q

QV= 有效变容二极管 Q

R情 商= 等效罐并联电阻

RS= 变容二极管串联电阻

VO= 有效值储罐电压

 

更宽的调谐范围通过两个众所周知的现象导致更大的振荡器相位噪声：谐振电路Q值的降低和调谐线上的噪声。为了实现更宽的调谐范围，变容二极管必须更多地耦合到谐振电路中。这种耦合降低了C的Q值V（有效可变电容）如公式2所示。C 的较低 Q 值V根据公式6，降低电箱的净Q值，从而增加相位噪声。

降低相位噪声的第二个因素是调谐输入端的热噪声，它会产生FM边带噪声。该噪声随着调谐范围的增加而增加，并且可能超过振荡器的固有相位噪声。由热噪声引起的相位噪声由下式给出：

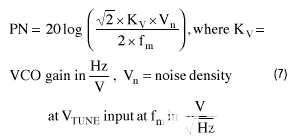
在这两种情况下，很明显，相位噪声会随着调谐范围的增加而降低。因此，为了在无微调VCO中保持低相位噪声，提供足够的调谐范围以满足保证带宽并适应预期的误差源至关重要。

随着变容二极管耦合得更频繁，变容二极管两端会出现更多的谐振电路电压摆幅，必须限制变容二极管的电压摆幅，以避免变容二极管正向偏置。这限制了谐振电路中的信号功率，从而限制了振荡器的相位噪声。最后，如果谐振电路等效串联电阻（ESR）过高，则可能会出现启动问题（参见公式）。具有非常宽频率调谐范围的VCO可能无法正常启动，尤其是在极端温度下。为了提供足够的调谐范围，问题是 - 多少？

振荡频率中的误差源

无微调VCO的频率调谐范围增加，以适应振荡频率中的误差源。这些误差源分为两类：元件值误差和设计居中误差。当然，设置振荡频率的LC元件并不理想。他们贡献了以下内容：

零件间差异（公差）

非理想性能（电感引起的频率响应有限， 引线中的电容和串联电阻）

电路中的寄生电容和电感引起的误差 布局

另一方面，设计居中误差是由于设计过程中VCO调谐范围的居中不确定性造成的。

元件公差误差

影响LC振荡器振荡频率的每个电容和电感元件的器件间精度有限，这种容差误差会导致振荡频率误差。表1列出了振荡器中频率设置元件的典型容差。

表 1.振荡器频率设置元件公差

 

元件	宽容
变容二极管	±15%在V调整= 0.4V， V 时为 ±10%调整= 2.4V
感应器	±5%
电容器	±5%
寄生电容	±10%
寄生电感	±6%
振荡器-器件阻抗	±15%

 

 

设计居中错误

设计居中经常被忽视，这是确定振荡频率的误差来源。为了最大限度地利用可用的频率调谐范围，调谐限值必须相对于所需的振荡频率对称。由于组件初始值或平均值建模不准确而导致的建立此中心点的任何错误都会减小可用于吸收误差源的调谐范围。为了保证温度、电源电压、元件容差等所有条件下的振荡频率，调谐范围必须足够宽以容纳该误差。

您可以使用振荡频率公式计算总频率误差，方法是将每个元素乘以变化比例因子：

计算由于各种误差引起的净频率偏差的最快方法是利用电子表格程序，该程序包含基于电路中的L和C值的振荡频率的详细公式。

频移和调谐范围

频率调谐范围，通过改变调谐电压从V获得调（低）到 V调（高），具有高频和低频端点 （f高和 f低） 具有“中心”频率 （f中心） 定义为 f 之间的中点高和 f低 （图5）。理想情况下，调谐范围应定位为 f中心在所需的振荡频率下（图5a）。但是，元件误差和以设计为中心的误差可能会改变频率调谐限制。

如果系统在最坏情况下提供的调谐电压不足，则无法达到所需的振荡频率，从而导致频率范围不足（图 5b）。显然，必须仔细确定所需的调谐范围。这是通过计算所有误差源引起的频率偏差并验证f低《 f理学学士。和 f高》 f理学学士。在最坏的情况下（图5c）。

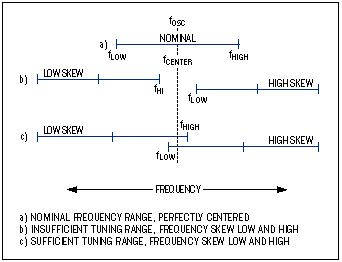
图5.调谐范围和频移。

设计验证

一旦电路板布局和元件值选择完成，设计就需要验证和测量（甚至比大多数RF电路还要多）。通常，您必须检查调谐范围、启动行为、相位噪声等是否符合设计目标。此外，必须在具有统计意义的制造运行次数上进行测量，以确定调谐范围和平均中心频率，以及其相对于所需振荡频率的位置。

所有这些工作对于生产具有所需电气性能的坚固、可重复的设计都是必要的。由于任务通常需要多次迭代，因此您可以轻松地花费数月时间才能实现可接受且值得生产的离散组件设计。开发无微调中频VCO需要详细的电路设计，包括所有误差源，在电路板上进行验证，并对生产进行监控，以确保可行的结果。Maxim推出了一款新型IC（将在第2部分介绍），解决了VCO设计问题，同时大幅缩短了实现免微调IFVCO所需的时间。