LVDT解调：整流器型与同步解调

　　了解两种解调方法的比较：同步解调和整流器型解调。在这里，我们将讨论每种方法的优点、缺点和适当的应用。

　　在上一篇文章中，我们讨论了

二极管整流解调器的工作原理和挑战。在本文中，我们将首先介绍整流器类型解调器的局限性。然后，我们将看到同步解调器可以解决其中的一些问题。最后，我们将探讨LVDT应用中同步解调的缺点。

　　整流型解调器的局限性

　　虽然精密整流器可以解决简单二极管整流器的挑战，但整流器型解调器通常有几个缺点。使用整流器型解调器时，我们需要访问LVDT次级的中心抽头，以整流每个次级绕组上的电压。因此，这种类型的解调仅适用于5线LVDT（图1（b））。

　　

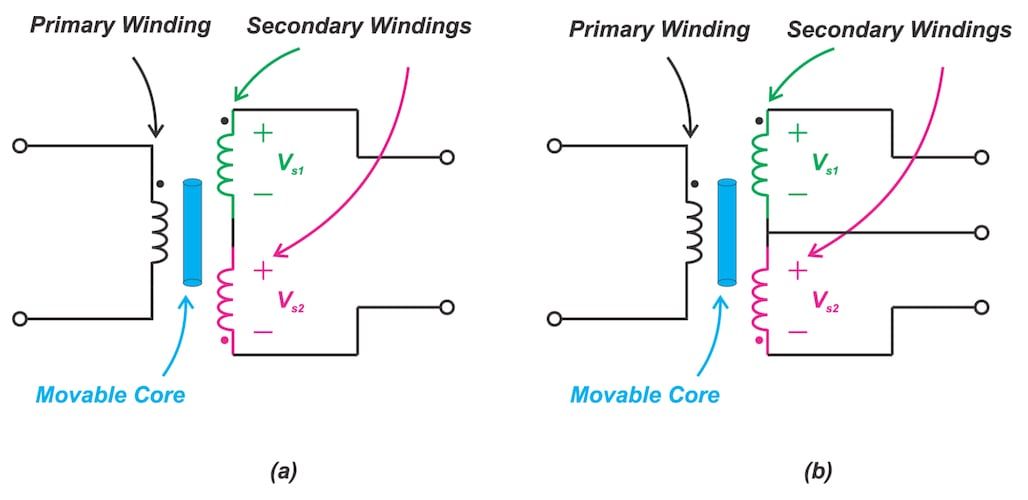
　　图1.（一） 4 线和 （二） 5 线 LVDT。

　　还有其他解调方法不需要访问中心抽头，可以通过处理两个次级之间的电压差来确定内核位置。这些解调器允许我们使用图1（a）所示的4线LVDT。

　　拥有最少数量的电气连接真的重要吗？

　　在许多应用中，调节电路距离传感器很远。一个很好的例子是在放射性应用的恶劣环境中进行测量，其中调节电路应放置在安全区域，甚至距离LVDT数百米。在这些情况下，通过5线配置长距离传输两个次级电压可能具有挑战性。由于调节模块远离LVDT，因此必须具有低分布电容的均衡布线。这意味着布线成本的大幅增加。

　　整流器型解调器的另一个缺点是噪声抑制有限。考虑一个LVDT传感器，其磁芯位移跟随250 Hz的正弦波形。图 2 中的红色曲线显示 该LVDT的解调输出

使用典型的二极管整流器获得。

　　

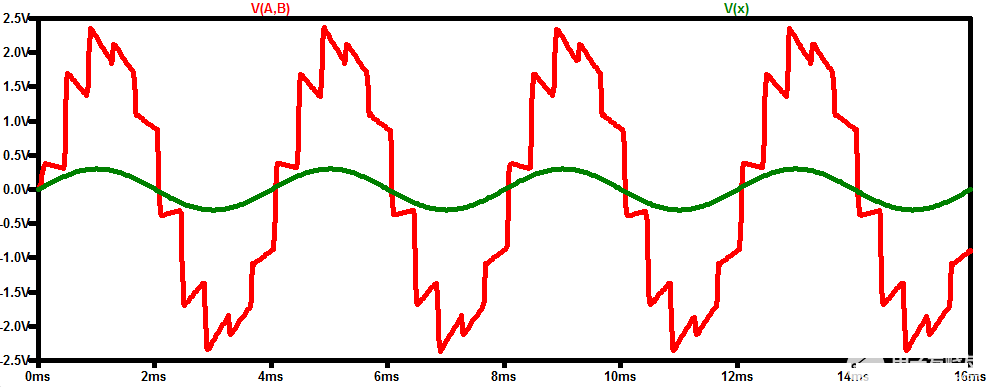
　　图2.

　　在此图中，绿色曲线显示了核心位移 x。如您所见，输出信号看起来像x的放大版本，只是它有一些与某些高频分量相对应的突然变化。

　　为了摆脱这些不需要的高频成分，我们可以使用截止频率略高于系统机械带宽（250 Hz）的低通滤波器。 因此，即使使用理想的低通滤波器，高达250
Hz的所有频率分量也将通过滤波器而不会衰减。 因此，耦合到传感器输出的任何低于250 Hz的噪声分量也将出现在解调器输出端。

　　噪声性能差是整流型解调器的一大缺点。 对于长电缆，这种限制变得更加明显。 噪声性能以及5线配置要求使该电路不适合长电缆敷设到偏远位置。 下面讨论的同步解调可以解决这两个问题。

　　同步解调

　　考虑图3所示的LVDT。 假设我们有 VEXC=Apcos（2π×fp×t）VEXC=Apcos（2π×fp×t）。

　　

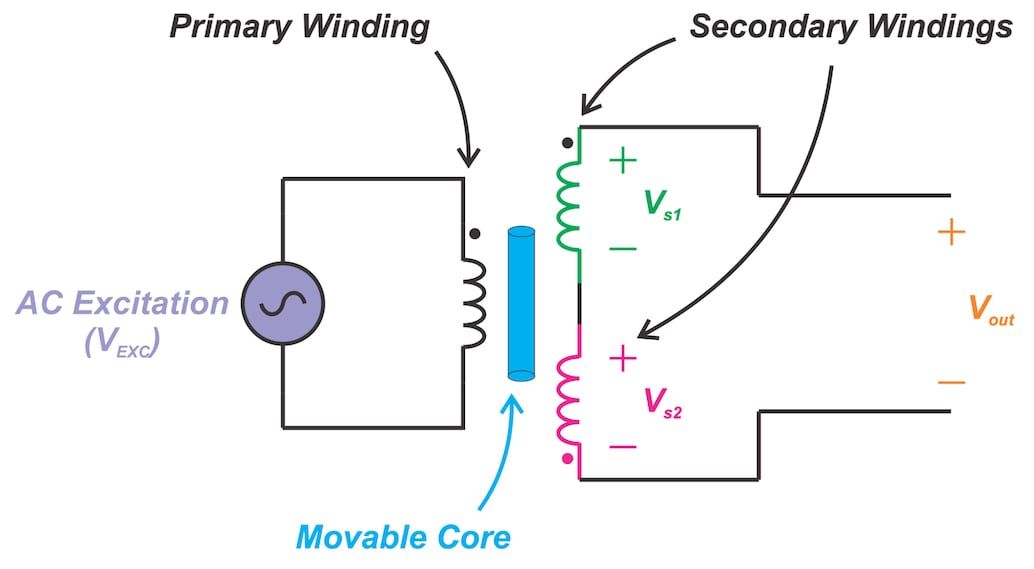
　　图3. LVDT 示例

　　差分输出（VoutVout）是调幅信号，可以表示为：

　　Vout=As×x×cos（2π×fp×t+φ）Vout=As×x×cos（2π×fp×t+φ）

等式 1.

　　其中 x 是核心位移，AsAs 是给出给定 x 的总输出幅度的比例因子。 相位项 ϕϕ 是由初级和次级电压之间的 LVDT
引起的相位差。 理想情况下，这种相移应该非常小，尤其是在制造商给出的特定频率附近。 但是，我们通常需要考虑这种相移。

　　同步解调技术将LVDT差分输出乘以激励信号（或一般与激励信号同步的信号）。 这给出了：

　　Vdemod=Vout×VEXC=As×x×cos（2π×fp×t+φ）×Apcos（2π×fp×t）Vdemod=Vout×VEXC=As×x×cos（2π×fp×t+φ）×Apcos（2π×fp×t）

等式2.

　　简化为：

　　Vdemod=12×As×x×Ap[cos（φ）+cos（2π×2fp×t+φ）]Vdemod=12×As×x×Ap[cos（φ）+cos（2π×2fp×t+φ）]

　　括号内的第一个项是直流，但是，第二项的激励频率是两倍。 因此，窄低通滤波器可以去除第二项，我们有：

　　Vfiltered=12×As×x×Apcos（φ）Vfiltered=12×As×x×Apcos（φ）

等式 3.

　　这为我们提供了与磁芯位移x成比例的直流电压。

　　通过乘以方波实现同步解调

　　我们可以使用模拟乘法器将LVDT输出乘以激励正弦波（公式2）; 然而，模拟乘法器价格昂贵，并且具有线性度限制。 我们可以将信号乘以与激励输入同步的方波，而不是乘以正弦波。

　　您可能想知道如何使用方波代替正弦波？ 在±1之间切换的方波可以表示为方波频率奇次谐波处的正弦波的无限和。 因此，频率 fpfp 的方波可以表示为：

　　vsquarewave（t）=∞∑n=1，3，54nπsin（2π×nfp×t）vsquarewave（t）=∑n=1，3，5∞4nπsin（2π×nfp×t）

　　当LVDT输出（fpfp处的正弦）乘以方波时，方波的基本分量（4πsin（2π×fp×t））（4πsin（2π×fp×t））产生直流分量和2fp2fp处的高频分量。 如上一节所述，高频分量将由低通滤波器抑制，所需的直流分量将出现在输出端。

　　乘以方波的高次谐波将产生
fpfp偶数倍的高频分量。 因此，直流分量是唯一出现在滤波器输出端的分量，就像将信号乘以正弦一样。 乘以方波的主要优点是可以显著简化解调器的电路实现。

　　同步解调器的电路实现

　　基于方波的同步解调器如图4所示。

　　

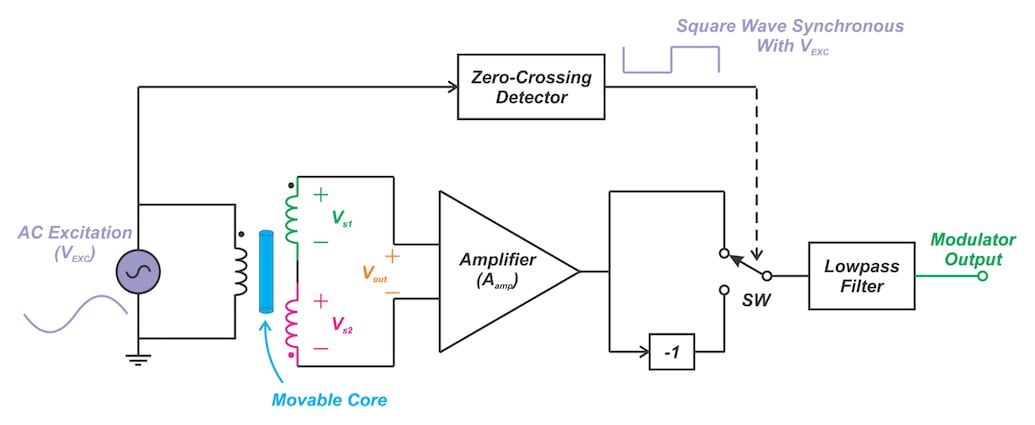
　　图4. 一种基于方波的同步解调器

　　在这种情况下，LVDT输出的放大版本乘以方波而不是激励正弦波。 方波与激励输入同步，通过“过零检测器”获得，如上框图所示。

　　为了执行方波乘法，信号链的增益在±Aamp±Aamp（AampAamp是放大器增益）之间周期性地变化。 请注意，较低的路径包含-1的增益。 这是通过使用方波驱动开关SW来实现的，该开关SW改变了上部和下部路径之间的信号路径。 这实际上相当于将放大器输出乘以方波。

　　最后，使用低通滤波器来保持输出的直流项并抑制高频分量。

　　LVDT同步解调器的优点

　　同步解调的主要优点是其噪声性能。 如上所述，同步解调频率将LVDT输出转换为DC，并使用低通滤波器来保持该DC分量。 低通滤波器将抑制其通带之外的所有噪声分量。

　　由于我们所需的信号在直流电，因此我们可以使用窄低通滤波器。 这将限制系统带宽，并允许解调器显著抑制耦合到LVDT输出的大部分噪声。 此外，通过同步解调，我们可以使用4线LVDT。

　　LVDT同步解调器的缺点

　　虽然与整流型解调器相比，同步解调可以提供更高的抗扰度，但其输出取决于激励电压的幅度（公式3中的ApAp）。 因此，对于同步解调，激励输入的幅度稳定性至关重要。

　　另一个问题是解调器输出取决于LVDT传递函数的相移（公式3中的cos（ϕ）cos（ϕ））。 理想情况下，这种相移应该非常小; 但是，它不是恒定的，可以随工作点而变化。 实用的解调器电路通常采用
相位补偿网络 调整产生的方波的相位。 补偿网络会增加解调器的复杂性。

　　然而，与整流器型解调器相比，这种增加的复杂性使得该电路适用于相对较长的电缆。 这是因为相移项ϕϕ可用于考虑接线引起的延迟。 因此，相位补偿电路也可用于补偿电缆延迟，并使电路适用于较长的电线。

　　其他解调技术

　　同步解调提供更高的抗噪性，只需要四个电气连接; 然而，它有其自身的局限性，例如依赖于激励输入的幅度以及相移问题。 为了解决这些问题，还有其他几种解调技术。 这些技术通常采用比率测量概念和基于DSP的方法来规避同步解调器的限制。