数控维恩桥振荡器的分析

在所有低频振荡器配置中，维也纳电桥是最容易使用的。它可靠，使用标准元件，提供良好的正弦波，并且相当不受设计所围绕的运算放大器类型的影响。然而，维也纳桥可能会被误解和过度简化，导致设计师感到沮丧。本文介绍了使用维恩桥振荡器的理论和实用性，以及如何使电路更稳定，更灵活。

维也纳桥振荡器电路

标准维恩桥振荡器的电路如图1所示。

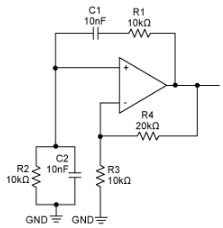
图1.标准维恩桥振荡器电路。

当振荡频率处的环路增益为单位，并且振荡频率处反馈信号的相移为零或2π的倍数时，电路保持振荡。

首先，需要考虑相移。在图1中，R1和C1相对于输出电压产生正相移电流。当该移相电流与R2和C2相遇时，后一种成分会产生负相移电压。在特定频率下，R1和C1引起的相移被R2和C2引起的相移抵消，因此净相移为零。发生这种情况时，电路有振荡的危险。

接下来，我们考虑由 R1、C1、R2 和 C2 组成的网络的传递函数。由于运算放大器的输出阻抗较低，且两个输入端的阻抗都非常高，因此确定Wien网络的传递函数（即，由顶部的R1和C1组成，底部由R2和C2组成的电阻分压器）相对简单。因此，传递函数为：

传递函数为：

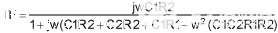
其中 j 表示传递函数中的 90 度相移（正或负）。其他（非“j”）项表示传递函数中的零相移。随着项的大小变化，由此产生的相移也会发生变化。等式1显示分母中的“非j”项等于零，分子和分母中仅剩j项。

将分子和分母除以 JW 不会留下 j 项，因此不会产生相移。因此，公式2计算了给定频率下零相移的条件。

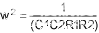
接下来，必须考虑收益。一旦解析了公式1中的项并确定了谐振频率，传递函数为：

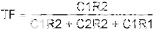
为了简化这一点，明智的做法是将 R1 等同于 R2，将 C1 等同于 C2。由此可见，在谐振时，从输出到输入的传递函数为：

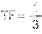
为了满足振荡要求（即零相移和单位增益），运算放大器电路需要具有3的增益，以克服Wien桥网络引起的衰减。从另一个角度来看，为了使两个运算放大器输入保持相同的电压，从输出到反相输入的电阻网络需要提供3的衰减，以匹配Wien网络的衰减。

从理论上讲，这种技术非常方便，但不实用。低容差电阻可轻松包含在设计中。然而，找到精确的电容器更加困难，并且包括精度大于20%的电容器可能成本高昂。因此，明智的做法是考虑不同电容值对电路性能的影响。

图2显示了一个简单的电子表格，说明了Wien桥网络的值及其对增益的影响。单元格B7是公式3中表示的传递函数，单元格B12由公式2确定（答案以kHz为单位），单元格B9是单元格B7的倒数。如果C1 = C2 = 10nF且R1 = R2 = 10kΩ，则电路振荡频率为1.59kHz，运算放大器增益等于3。该电路的实际测量支持这种计算。

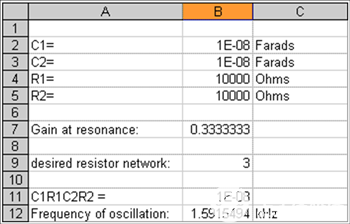
图2.维也纳桥组件值示例。

然而，上述结果是在容限为±10%的电容器上实现的。快速检查元件目录会发现，设计用于去耦的电容器非常相似，其容差为 -20%/+80%。在这种情况下，当C1 = 8nF （10nF -20%）和C2 = 18nF （10nF + 80%）时，电路需要4.25的增益。将这些元件插入设计会导致电路增益不足（仅提供3的增益）。因此，电路不会振荡。或者，如果C1为高电平，C2为低电平，则电路增益过大并振荡，但失真显著。此外，一旦电路振荡，由于电容值的容差很宽，频率就会不正确。理想的电路是偏置到振荡点的电路。增益越小，电路就会停止振荡;任何更多的收益，它开始扭曲。

如图3所示，反馈网络中的JFET解决了这个问题。使用JFET时，增益可以在很小的范围内变化，以确保一致的振荡。启动时，JFET 栅极电压为零;因此，漏源阻抗非常低。这种设计产生的增益大于3（以使电路正常工作）。一旦振荡累积，输出的整流负转换将为JFET的栅极提供关断电压。这会降低增益，电路稳定下来稳定振荡。输出幅度取决于两个二极管两端的压降，以及JFET的关断电压。遗憾的是，JFET的栅极关断电压变化很大，这导致电路的输出电压因批次而异。之所以选择TR1，是因为它的栅极关断电压变化非常小，从而保证了电路之间输出电压的微小变化。但该TR1电路通常不会产生失真最低的振荡器。事实上，电路振荡，但失真明显;无论失真如何，JFET 都能保持这种振荡。因此，JFET只能用作保持电路运行的辅助工具，而不是补偿不良的电路设计。

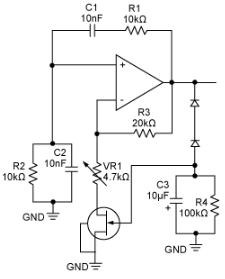
图3.在反馈网络中带有结栅场效应晶体管（JFET）的维也纳桥振荡器。

除非可以容忍复杂的电路设计，否则确保电路启动并继续振荡而不会失真（由于增益过大）的最简单方法是在反馈路径中插入一个可变电阻。然后将电阻调整到电路刚开始振荡的点。这提供了失真最低的干净正弦波。

尽管一些工程师认为可变电阻器是一种简单的设计解决方案，但制造工程师认为这是一个耗时的生产难题。调整可变电阻需要时间和人力，使电路复杂且生产成本高昂。

解决这一困境的理想解决方案是插入一个电子可变电阻器或数字电位器（digipot）。在图3中，用数字电位器代替可变电阻VR1提供了一种低成本、小型、简单的解决方案，可以在生产过程中调整电路，以确保最小的失真。该数字电位器可以单独使用，也可以与其他电阻串联或并联使用，以微调增益。一旦电路振荡，JFET就会提供精细的增益修改，使电路保持运行。

在图3所示电路中，MAX5467 10kΩ数字电位器可以代替可变电阻VR1。由于该部件具有两个浮动端子，因此不必以地面为参考。插入额外的MAX5467器件与R1和R2串联，使用户能够调整电路的频率。数字电位器具有简单的数字接口，这意味着无需微控制器即可手动调整电路。

将两个10kΩ数字电位器与电阻R1和R2串联插入，电路的工作频率可在833Hz至1.6kHz范围内调节。此外，一旦插入10kΩ数字电位器代替VR1，电路的输出就可以随着电路增益的变化从直流到纯正弦波和失真正弦波进行电子调节。

图4所示为最终电路，包括MAX5467数字电位器。图5所示为交流接地和JEFT偏置电路。图6和图7分别显示了频率和增益调整电路。数字电位器由符号IC2，IC3和IC4表示。IC2和IC3共享相同的数字接口，因此可以同时递增和递减。IC4提供独立的增益调整电路。

为了进一步线性化JFET的特性，在栅极周围增加了两个100kΩ电阻。这些电阻为JFET提供一些负反馈，从而平滑JFET性能的非线性。

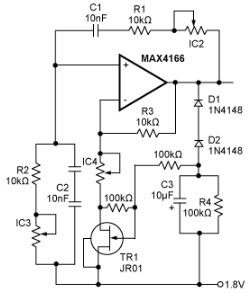
图4.在反馈网络中带有JFET和数字电位器的维恩桥振荡器。

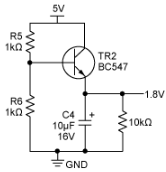
图5.交流接地和JFET偏置电路。

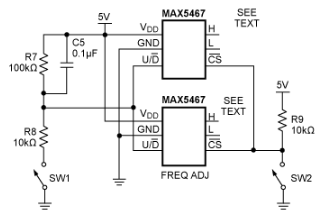
图6.采用MAX5467的频率调整电路。

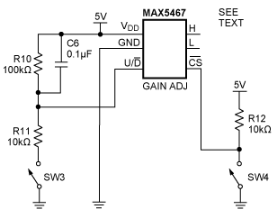
图7.采用MAX5467的增益调节电路

进一步实验

本文分析了维恩桥振荡器的要点以及许多振荡器设计的基础知识。如果没有正确掌握基础知识，在维也纳桥周围添加的任何电路都只会掩盖错误。

但是，可以通过更仔细地检查电路并添加额外的电路来进一步提高性能来进行改进。

反馈环路会导致失真。二极管正向电压随温度漂移（2.1mV/°C）。这直接影响输出电压。此外，JFET偏置电压随温度变化。这些电压漂移可以通过在输出端增加RMS-DC转换器或峰值电平检波器来克服。这种电路需要产生与正弦波输出成比例的精确直流输出电压。如果该直流信号反相（使用简单的运算放大器电路）并直接馈送到JFET输入端，则可以使正弦波输出更加稳定。

结论

维恩桥振荡器在理论上很容易理解，但电路的实用性可能会使设计人员感到沮丧。在电路的三个关键区域插入数字电位器可确保更稳定的操作和工厂/用户的可调节性。

审核编辑：郭婷