均衡技术使DAC频率响应趋平化

数模转换器（DAC）在仪器仪表和无线通信等应用中将数字数据转换为模拟电压或电流。DAC的输出频率范围一般为直流至小于fS/2，其中 fS是输入更新频率。然而，大多数DAC的输出频率响应根据sin（x）/x （sinc）频率响应包络滚降。

在图1的通用示例中，数字基带信号由DAC采样。DAC的频率响应不平坦，在较高频率下会衰减模拟输出。在 f 的 80%奈奎斯特，例如（f奈奎斯特= fS/2），频率响应衰减2.42dB。对于一些需要平坦频率响应的宽带应用来说，这种损耗是不可接受的。然而，幸运的是，有几种技术可用于应对DAC的非平坦频率响应。这些措施包括提高DAC的更新速率，以及使用插值技术、前均衡滤波和后均衡滤波，所有这些都会降低或消除sinc滚降的影响。

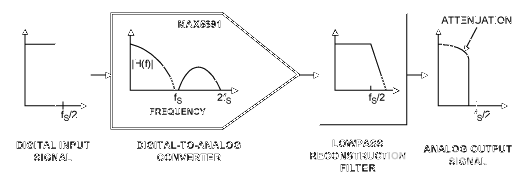
图1.DAC的非平坦频率响应会衰减输出信号，尤其是在高频时。

了解DAC频率响应

要了解DAC的非平坦频率响应，请将DAC输入视为时域中的一系列脉冲（图2a）和频域中的相应频谱（图2b）。实际DAC输出为“零阶保持”（图2c），可在1/f的更新周期内保持电压恒定S.在频域中，这种零阶保持会引入sin（x）/x失真（也称为孔径失真）[1].如图2d所示，输出信号频谱的幅度乘以|sin（x）/x|（sinc包络），其中x = πf / fS.得到的频率响应如公式1所示，并绘制于图3中。因此，孔径失真的作用类似于LPF，它衰减了镜像频率，但也衰减了所需的带内信号。

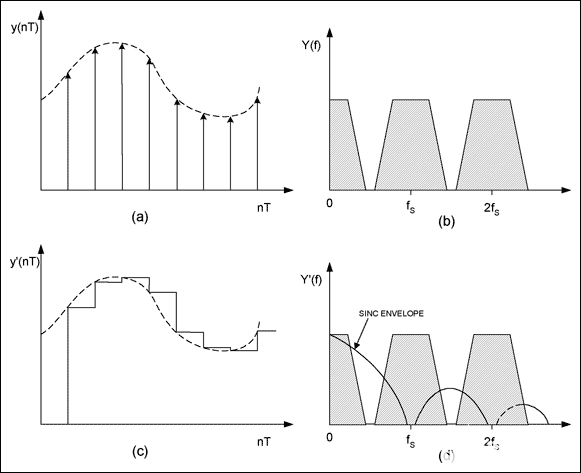
图2.DAC的理想输出是时域（a）中的一系列电压脉冲和频域（b）中的一系列图像光谱。实际DAC使用零阶保持将输出电压保持一个更新周期（c），这会导致sinc包络（d）的输出信号衰减。

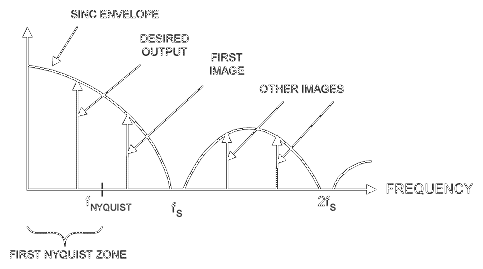
图3.DAC输出在频域中的这种表示表明，所需信号通常在第一奈奎斯特区内，但许多图像信号存在于更高的频率下。

sin（x）/x （sinc） 函数在数字信号处理中是众所周知的。对于DAC，输入为脉冲，输出为恒压脉冲，更新周期为1/f。S（脉冲响应），其幅度会根据输入端的下一个脉冲而突然变化。DAC的频率响应是通过脉冲响应（电压脉冲）的傅里叶变换获得的。脉冲的傅里叶变换采用 H（f） = sin（pf/f 的一般形式S）/（pf/fS)[2]:

如图3所示，第一奈奎斯特区中所需的信号频率作为镜像反射到f之间的第二奈奎斯特区S/2和 fS，但其幅度被sinc函数衰减。图像信号也出现在较高的奈奎斯特区。通常，这些镜像频率必须通过低通（LPF）或带通滤波器（BPF）（通常称为重建滤波器）来消除或衰减。这种滤波器类似于模数转换器通常需要的抗混叠滤波器。

当DAC输出频率接近其更新频率fS，频率响应接近零或零（图 3）。因此，DAC的输出衰减取决于其更新速率（参见公式1）。0.1dB频率平坦度约为0.17f奈奎斯特，其中 f奈奎斯特= fS/2.当输出频率接近fS/2，第一个镜像频率也是如此（图3）。因此，最大可用DAC输出频率（对于通过滤波去除镜像频率的系统）约为f的80%奈奎斯特.

第一个图像频率为 f图像= fS， G外.在 f外= 0.8f奈奎斯特， f图像= 1.2f奈奎斯特，只剩下0.4f奈奎斯特在频率音调之间，滤波器删除图像。输出频率高于 f 的 80%奈奎斯特使滤波器难以去除镜像，但可用频率输出的降低允许实现重建滤波器的设计。

提高更新率？

在 f 的 80%奈奎斯特，输出幅度衰减2.42dB。对于需要平坦频率响应的宽带应用，这种衰减是不可接受的。由于DAC的输出衰减取决于其更新速率，因此只需提高转换器的更新速率并保持输入信号带宽不变，即可将sinc滚降的影响降至最低，并将0.1dB平坦度推至更高的频率。

提高DAC的更新速率不仅可以降低非平坦频率响应的影响，还可以降低量化本底噪声（大多数DAC数据手册的噪声频谱密度表示），并放宽对重建滤波器的要求。缺点包括DAC成本较高，功耗较高，以及需要更快的数据处理。然而，更高更新率的好处是如此重要，以至于制造商不得不引入插值技术。插值DAC具有更高更新速率的所有优点，同时将输入数据速率保持在较低的频率。

插话？

插值DAC包括一个或多个数字滤波器，它们在每个现有数据样本之后插入一个样本。在时域中，插值器为输入的每个数据样本填充一个额外的数据样本，并在每对连续的数据样本值之间插值。数据样本总数增加两倍，因此DAC的更新速度必须快两倍。

The MAX5895[3]例如，包含三个插值级以实现8倍插值（DAC的更新速率是数据速率的8倍）。这种技术提高了更新速率，同时保持了较低的频率。在频域中，sinc频率响应也移出8倍，有效镜像频率移出8倍，这放宽了对重建滤波器的要求。

预均衡？

提高更新速率会降低但不能消除频率滚降的影响。如果您已经在使用最快的DAC，则必须选择其他技术来减少DAC的频率滚降。例如，可以设计一个数字滤波器，其频率响应是sinc函数的倒数，即1/sinc（x）。理论上，这种预均衡滤波器消除了sinc频率响应的影响，从而产生完全平坦的整体频率响应。预均衡滤波器首先滤除数字输入数据以均衡基带信号，然后将数据发送到DAC。通过消除DAC输出端的同步衰减，可以在不衰减的情况下重建原始信号（图4a）。

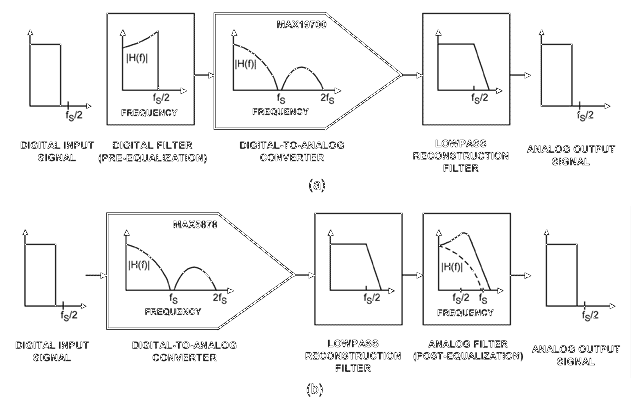
图4.预均衡数字滤波器用于消除DAC （a）中sinc滚降的影响。作为替代方案，您可以使用后均衡模拟滤波器来实现相同的目的（b）。

频率响应与sinc函数相反的任何数字滤波器都将均衡DAC固有的sinc频率响应。但是，由于sinc频率响应不是一阶，因此首选有限脉冲响应（FIR）数字滤波器[1].频率采样技术用于设计FIR滤波器。假设信号位于第一奈奎斯特区，则频率响应（H（f））从直流采样至0.5fS（图5）。使用傅里叶逆变换，然后将频率采样点（H（k））转换为时域中的脉冲响应。脉冲响应系数为：

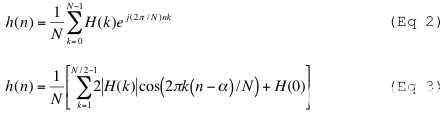
其中 H（k） 和 k = 0， 1， ...N-1代表理想或目标频率响应。数量 h（n） 和 n = 0， 1， ...N-1是H（k）在时域中的脉冲响应，= 

（N-1）/2。对于具有正对称性和偶数N的线性相位FIR滤波器，可以使用公式3简化h（n）[1].对于奇数值 N，求和中的上限为 （N-1）/2。

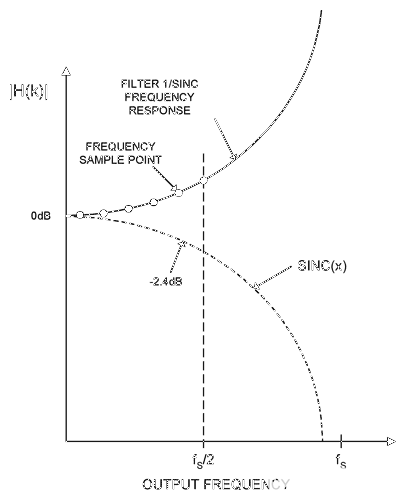
图5.通过对从直流到f的反sinc频率响应进行采样来设计数字预均衡滤波器S/2.

增加H（k）的频率采样点（N）的数量会产生更接近目标响应的频率响应。采样点太少的滤波器会降低均衡器的有效性，因为它会产生与目标频率响应的较大偏差。另一方面，具有太多采样点的滤波器需要更多的数字处理能力。一个好的技术是使用大N计算h（n），将h（n）截断为少量点，然后应用窗口平滑h（n）并产生准确的频率响应。

图 6 所示的滤波器使用 N = 800 来计算 h（n）。然后，将 h（n） 截断为仅 100 磅，并将 Blackman 窗口应用于 h（n）。结合FIR滤波器和DAC sinc响应的频率响应（图6中的顶部曲线）表现出0.1dB的平坦度，接近奈奎斯特频率（即，约96%的f）奈奎斯特，其中fNYQUIST= fS/2)).相比之下，未补偿的DAC响应（底部曲线）仅将0.1dB平坦度保持在f的17%奈奎斯特.由于滤波器增益大于单位增益，因此必须确保滤波器的输出幅度不超过DAC允许的最大输入电平。

图6.图5中设计的FIR滤波器可均衡DAC的sinc响应，并实现0.1dB平坦度，高达96%f。奈奎斯特.

使用公式3获得脉冲响应系数后，可以使用标准数字处理技术实现FIR滤波器。也就是说，h（n） 滤除输入信号数据 x（n），如公式 4 所示：

补偿DAC的动态性能低于未补偿DAC，因为在较高输入频率下获得更高的增益要求您有意降低信号电平以避免削波输入。假设输入是 DC 和 f 之间的单音.MAX（< fS/2），衰减取决于f.MAX:

其中 V集成电路是补偿DAC的输入电压，V裁判是基准电压。例如，如果最大预期输入频率为 f.MAX= 0.8f奈奎斯特，DAC输入必须被噪声和热噪声衰减。补偿DAC的最大SNR是恒定的，与频率无关，但取决于最大预期输出频率：

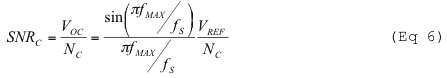
其中 V超频是输出振幅。

对于未补偿DAC，输出信号由sinc包络衰减：

未补偿DAC的噪声功率与补偿DAC相同。因此，最大未补偿DAC SNR为：

补偿DAC SNR的退化是通过对SNR进行除法来发现的：

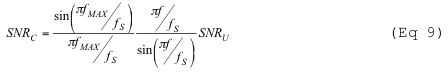
与未补偿DAC不同，补偿DAC SNR的退化与频率有关。在较低频率下比在f频率下退化更严重.MAX.

后均衡？

在目标输出频带上均衡DAC的sinc频率响应的另一种方法是添加一个模拟滤波器，其频率响应近似等于sinc函数的倒数。许多这样的模拟均衡滤波器被设计用于均衡传输线和放大器。这些技术可以用于减少DAC不需要的sinc响应的影响。后均衡滤波器插入DAC的重建滤波器之后（图4b）。

本应用采用图7a所示的简单有源均衡器。对于给定带宽，选择R1、R2和C1，以便模拟均衡器的频率响应抵消DAC的sinc频率响应。SPICE仿真软件可以帮助优化给定应用的频率平坦度。典型模拟均衡器的频率响应（图7b）显示，0.1dB平坦度扩展到f的50%以上奈奎斯特.如果没有后均衡滤波器，0.1dB平坦度仅扩展到f的17%fNYQUIST.注意，图7a中的最大电路增益为（1+R1/R2）。

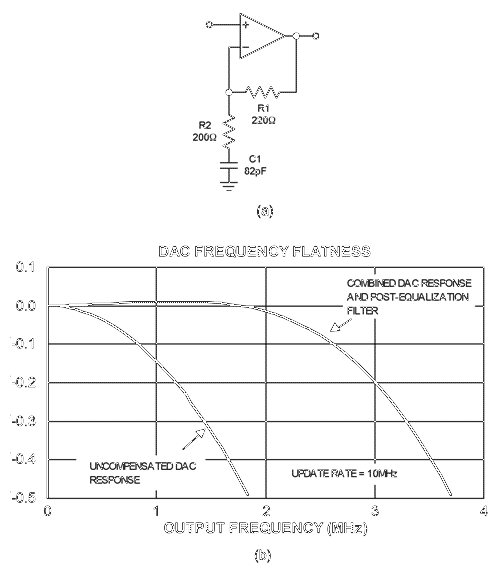
图7.用于降低DAC sinc滚降的影响，这种简单的有源模拟均衡器（a）将0.1dB平坦度从17%提高到50% f奈奎斯特 (b）。

后均衡滤波器会影响DAC的SNR，因为它会在较高频率下放大噪声。假设未补偿DAC中的噪声受到量化噪声的限制，则输出信号和噪声一起被sinx/x包络衰减。然而，使用后均衡滤波器时，输出信号幅度和噪声密度在整个频率范围内是恒定的（假设补偿完美）。补偿和未补偿DAC的输出噪声是通过将近直流至f的噪声功率积分来获得的奈奎斯特:

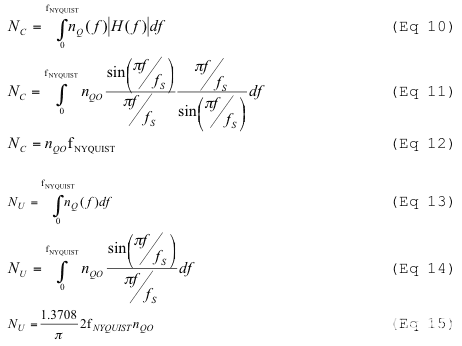
其中H（f）是后均衡滤波器的频率响应，nQ（f）是噪声功率密度，n质量质量是直流附近的未衰减量化噪声密度，NC和NU分别是补偿和未补偿DAC的总噪声功率。最大SNR归一化为基准电压V裁判.请记住，fNYQUIST等于 fS/2.然后，信噪比为：

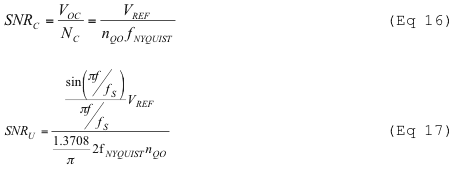
同样，将两个SNR相除以未补偿SNR得到补偿SNR。最大信噪比C在较低频率下会降低，但在较高频率下会改善：

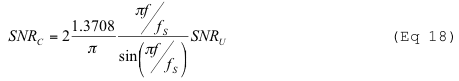
到目前为止，DAC的重建滤波器被认为是理想的LPF：其频率响应平坦到f奈奎斯特，然后突然下降到零。实际上，重建滤波器还会在其截止频率附近增加滚降。因此，前面讨论的均衡前和后均衡技术可以用于另一个目的，即均衡重建滤波器中的任何滚降。

总结

DAC固有的sinc频率响应的影响会衰减输出信号，特别是在较高频率下，由此产生的非平坦频率响应会降低宽带应用中的最大有用带宽。较高的更新速率会使频率响应趋于平缓，但较高的更新速率也会增加DAC的成本和复杂性。

预均衡技术采用数字滤波器在将数据发送到DAC之前对其进行处理，提供0.1dB频率平坦度至96%f。fNYQUIST（fNYQUIST= fS/2），但需要额外的数字处理。（相比之下，未补偿DAC仅提供0.1dB平坦度至f的17%fNYQUIST.)另一种技术增加了一个后均衡模拟滤波器来均衡DAC的输出，并在f的50%下实现0.1dB平坦度奈奎斯特，但需要额外的硬件。两种补偿技术均可在低输出频率下降低SNR。

审核编辑：郭婷