

决策规划,全局路径规划常用算法
描述
正菜之前,我们先来了解一下图(包括有向图和无向图)的概念。图是图论中的基本概念,用于表示物体与物体之间存在某种关系的结构。在图中,物体被称为节点或顶点,并用一组点或小圆圈表示。节点间的关系称作边,可以用直线或曲线来表示节点间的边。
如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边,如图10所示。在有向图中,与一个节点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。相反,边没有方向的图称为无向图。
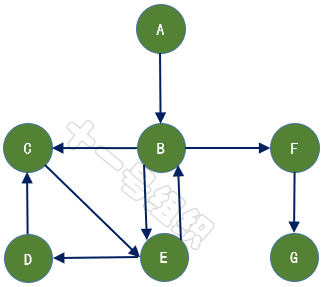
图10 有向图示例
数学上,常用二元组G =(V,E)来表示其数据结构,其中集合V称为点集,E称为边集。对于图6所示的有向图,V可以表示为{A,B,C,D,E,F,G},E可以表示为{,,,,,,}。表示从顶点A发向顶点B的边,A为始点,B为终点。
在图的边中给出相关的数,称为权。权可以代表一个顶点到另一个顶点的距离、耗费等,带权图一般称为网。
在全局路径规划时,通常将图11所示道路和道路之间的连接情况,通行规则,道路的路宽等各种信息处理成有向图,其中每一个有向边都是带权重的,也被称为路网(Route Network Graph)。
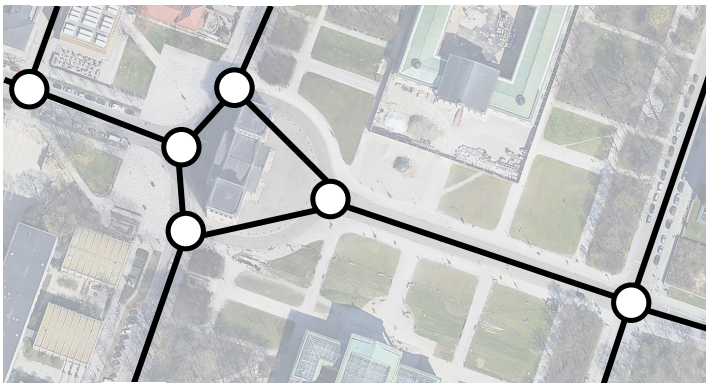
图11 道路连接情况
那么,全局路径的规划问题就变成了在路网中,搜索到一条最优的路径,以便可以尽快见到那个心心念念的她,这也是全局路径规划算法最朴素的愿望。而为了实现这个愿望,诞生了Dijkstra和A*两种最为广泛使用的全局路径搜索算法。
Dijkstra算法
戴克斯特拉算法(Dijkstra’s algorithm)是由荷兰计算机科学家Edsger W. Dijkstra在1956年提出,解决的是有向图中起点到其他顶点的最短路径问题。
假设有A、B、C、D、E、F五个城市,用有向图表示如图12,边上的权重代表两座城市之间的距离,现在我们要做的就是求出起点A城市到其它城市的最短距离。
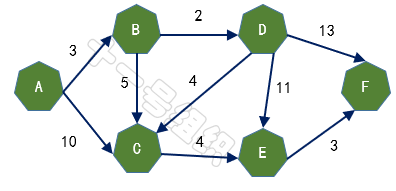
图12 五个城市构建的有向图
用Dijkstra算法求解步骤如下:
(1)创建一个二维数组E来描述顶点之间的距离关系,如图13所示。E[B][C]表示顶点B到顶点C的距离。自身之间的距离设为0,无法到达的顶点之间设为无穷大。
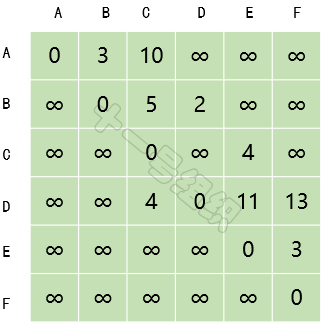
图13 顶点之间的距离关系
(2)创建一个一维数组Dis来存储起点A到其余顶点的最短距离。一开始我们并不知道起点A到其它顶点的最短距离,一维数组Dis中所有值均赋值为无穷大。接着我们遍历起点A的相邻顶点,并将与相邻顶点B和C的距离3(E[A][B])和10(E[A][C])更新到Dis[B]和Dis[C]中,如图14所示。这样我们就可以得出起点A到其余顶点最短距离的一个估计值。
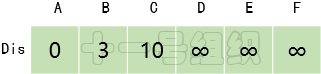
图14 Dis经过一次遍历后得到的值
(3)接着我们寻找一个离起点A距离最短的顶点,由数组Dis可知为顶点B。顶点B有两条出边,分别连接顶点C和D。因起点A经过顶点B到达顶点C的距离8(E[A][B] + E[B][C] = 3 + 5)小于起点A直接到达顶点C的距离10,因此Dis[C]的值由10更新为8。同理起点A经过B到达D的距离5(E[A][B] + E[B][D] = 3 + 2)小于初始值无穷大,因此Dis[D]更新为5,如图15所示。
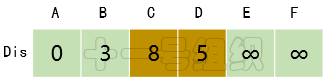
图15 Dis经过第二次遍历后得到的值
(4)接着在剩下的顶点C、D、E、F中,选出里面离起点A最近的顶点D,继续按照上面的方式对顶点D的所有出边进行计算,得到Dis[E]和Dis[F]的更新值,如图16所示。
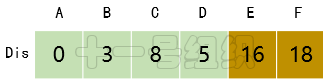
图16 Dis经过第三次遍历后得到的值
(5)继续在剩下的顶点C、E、F中,选出里面离起点A最近的顶点C,继续按照上面的方式对顶点C的所有出边进行计算,得到Dis[E]的更新值,如图17所示。
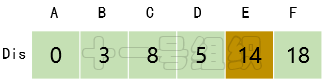
图17 Dis经过第四次遍历后得到的值
(6)继续在剩下的顶点E、F中,选出里面离起点A最近的顶点E,继续按照上面的方式对顶点E的所有出边进行计算,得到Dis[F]的更新值,如图18所示。
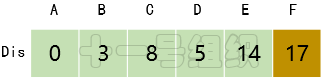
图18 Dis经过第五次遍历后得到的值
(6)最后对顶点F所有点出边进行计算,此例中顶点F没有出边,因此不用处理。至此,数组Dis中距离起点A的值都已经从“估计值”变为了“确定值”。
基于上述形象的过程,Dijkstra算法实现过程可以归纳为如下步骤:
(1)将有向图中所有的顶点分成两个集合P和Q,P用来存放已知距离起点最短距离的顶点,Q用来存放剩余未知顶点。可以想象,一开始,P中只有起点A。同时我们创建一个数组Flag[N]来记录顶点是在P中还是Q中。对于某个顶点N,如果Flag[N]为1则表示这个顶点在集合P中,为1则表示在集合Q中。
(2)起点A到自己的最短距离设置为0,起点能直接到达的顶点N,Dis[N]设为E[A][N],起点不能直接到达的顶点的最短路径为设为∞。
(3)在集合Q中选择一个离起点最近的顶点U(即Dis[U]最小)加入到集合P。并计算所有以顶点U为起点的边,到其它顶点的距离。例如存在一条从顶点U到顶点V的边,那么可以通过将边U->V添加到尾部来拓展一条从A到V的路径,这条路径的长度是Dis[U]+e[U][V]。如果这个值比目前已知的Dis[V]的值要小,我们可以用新值来替代当前Dis[V]中的值。
(4)重复第三步,如果最终集合Q结束,算法结束。最终Dis数组中的值就是起点到所有顶点的最短路径。
A*算法
1968年,斯坦福国际研究院的Peter E. Hart, Nils Nilsson以及Bertram Raphael共同发明了A*算法。A*算法通过借助一个启发函数来引导搜索的过程,可以明显地提高路径搜索效率。
下文仍以一个实例来简单介绍A*算法的实现过程。如图19所示,假设小马要从A点前往B点大榕树底下去约会,但是A点和B点之间隔着一个池塘。为了能尽快提到达约会地点,给姑娘留下了一个守时踏实的好印象,我们需要给小马搜索出一条时间最短的可行路径。
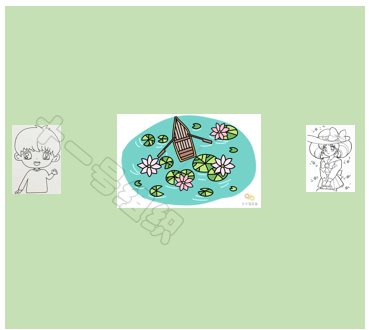
图19 约会场景示意图
A*算法的第一步就是简化搜索区域,将搜索区域划分为若干栅格。并有选择地标识出障碍物不可通行与空白可通行区域。一般地,栅格划分越细密,搜索点数越多,搜索过程越慢,计算量也越大;栅格划分越稀疏,搜索点数越少,相应的搜索精确性就越低。
如图20所示,我们在这里将要搜索的区域划分成了正方形(当然也可以划分为矩形、六边形等)的格子,图中蓝色格子代表A点(小马当前的位置),紫色格子代表B点(大榕树的位置),灰色格子代表池塘。同时我们可以用一个二维数组S来表示搜素区域,数组中的每一项代表一个格子,状态代表可通行和不可通行。
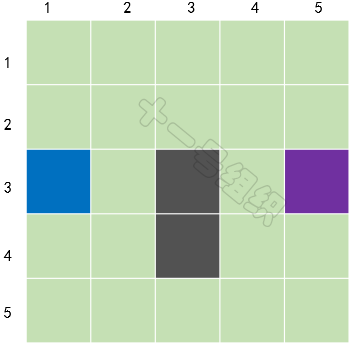
图20 经过简化后的搜索区域
接着我们引入两个集合OpenList和CloseList,以及一个估价函数F = G + H。OpenList用来存储可到达的格子,CloseList用来存储已到达的格子。G代表从起点到当前格子的距离,H表示在不考虑障碍物的情况下,从当前格子到目标格子的距离。F是起点经由当前格子到达目标格子的总代价,值越小,综合优先级越高。
G和H也是A*算法的精髓所在,通过考虑当前格子与起始点的距离,以及当前格子与目标格子的距离来实现启发式搜索。对于H的计算,又有两种方式,一种是欧式距离,一种是曼哈顿距离。
欧式距离用公式表示如下,物理上表示从当前格子出发,支持以8个方向向四周格子移动(横纵向移动+对角移动)。
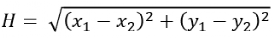
曼哈顿距离用公式表示如下,物理上表示从当前格子出发,支持以4个方向向四周格子移动(横纵向移动)。这是A*算法最常用的计算H值方法,本文H值的计算也采用这种方法。
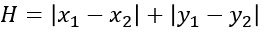
现在我们开始搜索,查找最短路径。首先将起点A放入到OpenList中,并计算出此时OpenList中F值最小的格子作为当前方格移入到CloseList中。由于当前OpenList中只有起点A这个格子,所以将起点A移入CloseList,代表这个格子已经检查过了。
接着我们找出当前格子A上下左右所有可通行的格子,看它们是否在OpenList当中。如果不在,加入到OpenList中计算出相应的G、H、F值,并把当前格子A作为它们的父节点。本例子,我们假设横纵向移动代价为10,对角线移动代价为14。
我们在每个格子上标出计算出来的F、G、H值,如图21所示,左上角是F,左下角是G,右下角是H。通过计算可知S[3][2]格子的F值最小,我们把它从OpenList中取出,放到CloseList中。
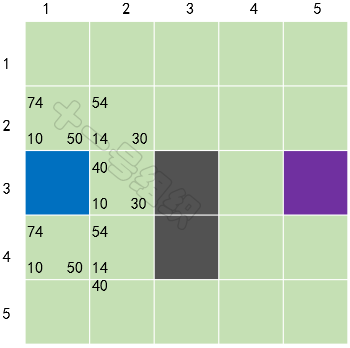
图21 第一轮计算后的结果
接着将S[3][2]作为当前格子,检查所有与它相邻的格子,忽略已经在CloseList或是不可通行的格子。如果相邻的格子不在OpenList中,则加入到OpenList,并将当前方格子S[3][2]作为父节点。
已经在OpenList中的格子,则检查这条路径是否最优,如果非最优,不做任何操作。如果G值更小,则意味着经由当前格子到达OpenList中这个格子距离更短,此时我们将OpenList中这个格子的父节点更新为当前节点。
对于当前格子S[3][2]来说,它的相邻5个格子中有4个已经在OpenList,一个未在。对于已经在OpenList中的4个格子,我们以它上面的格子S[2][2]举例,从起点A经由格子S[3][2]到达格子S[2][2]的G值为20(10+10)大于从起点A直接沿对角线到达格子S[2][2]的G值14。显然A经由格子S[3][2]到达格子S[2][2]不是最优的路径。当把4个已经在OpenList 中的相邻格子都检查后,没有发现经由当前方格的更好路径,因此我们不做任何改变。
对于未在OpenList的格子S[2][3](假设小马可以斜穿墙脚),加入OpenList中,并计算它的F、G、H值,并将当前格子S[3][2]设置为其父节点。经历这一波骚操作后,OpenList中有5个格子,我们需要从中选择F值最小的那个格子S[2][3],放入CloseList中,并设置为当前格子,如图22所示。
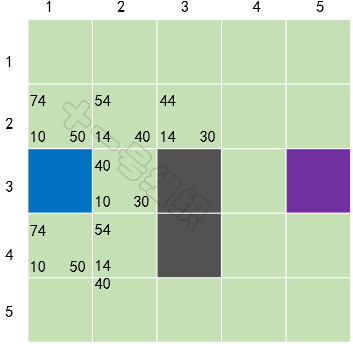
图22 第二轮计算后的结果
重复上面的故事,直到终点也加入到OpenList中。此时我们以当前格子倒推,找到其父节点,父节点的父节点……,如此便可搜索出一条最优的路径,如图23中红色圆圈标识。
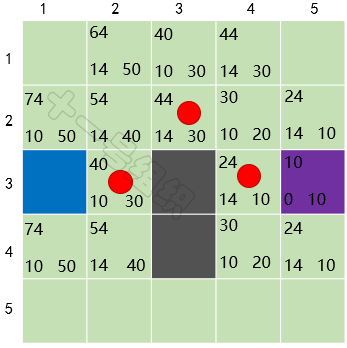
图23 最后计算得到的结果
基于上述形象的过程,A*算法实现过程可以归纳为如下步骤:
(1)将搜索区域按一定规则划分,把起点加入OpenList。
(2)在OpenList中查找F值最小的格子,将其移入CloseList,并设置为当前格子。
(3)查找当前格子相邻的可通行的格子,如果它已经在OpenList中,用G值衡量这条路径是否更好。如果更好,将该格子的父节点设置为当前格子,重新计算F、G值,如果非更好,不做任何处理;如果不在OpenList中,将它加入OpenList中,并以当前格子为父节点计算F、G、H值。
(4)重复步骤(2)和步骤(3),直到终点加入到OpenList中。
两种算法比较
Dijkstra算法的基本思想是“贪心”,主要特点是以起点为中心向周围层层扩展,直至扩展到终点为止。通过Dijkstra算法得出的最短路径是最优的,但是由于遍历没有明确的方向,计算的复杂度比较高,路径搜索的效率比较低。且无法处理有向图中权值为负的路径最优问题。
A*算法将Dijkstra算法与广度优先搜索(Breadth-First-Search,BFS)算法相结合,并引入启发函数(估价函数),大大减少了搜索节点的数量,提高了搜索效率。但是A*先入为主的将最早遍历路径当成最短路径,不适用于动态环境且不太适合高维空间,且在终点不可达时会造成大量性能消耗。
图24是两种算法路径搜索效率示意图,左图为Dijkstra算法示意图,右图为A*算法示意图,带颜色的格子表示算法搜索过的格子。由图24可以看出,A*算法更有效率,手术的格子更少。
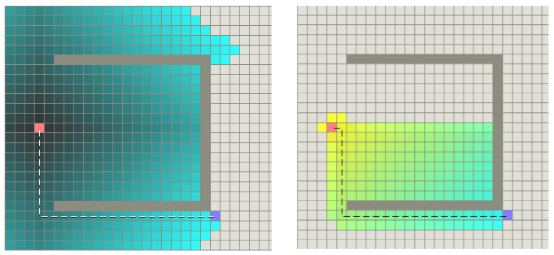
图24 Dijkstra算法和A*算法搜索效率对比图(图片来源:https://mp.weixin.qq.com/s/myU204Uq3tfuIKHGD3oEfw)
审核编辑 :李倩
-
多台仓储AGV协作全局路径规划算法的研究2024-10-28 1226
-
全局路径规划RRT算法原理2023-11-24 2010
-
无人驾驶汽车的路径规划与跟随控制算法案例2023-07-19 1187
-
自动驾驶轨迹规划之路径规划总结2023-06-07 820
-
决策规划系列:运动规划常用算法2023-04-17 2101
-
为ROS navigation功能包添加自定义的全局路径规划器(Global Path Planner)2021-05-16 4828
-
机器人路径规划算法,全局路径规划与局部路径规划究竟有哪些区别2020-12-26 6200
-
解析自动驾驶汽车路径规划算法2020-07-28 5565
-
机器人路径规划技术解读2019-09-06 3177
-
基于路径跟踪方法的路径规划算法2017-12-04 1523
-
基于游戏中NPC路径规划的混合算法2017-11-14 1067
-
路径规划 人工势场2017-05-15 4248
-
基于势场栅格法的机器人全局路径规划2015-11-30 534
-
遗传算法在水下机器人路径规划中的应用2010-03-03 685
全部0条评论

快来发表一下你的评论吧 !

