使用Python分析拉普拉斯空间中的二阶电路

　　了解如何使用拉普拉斯变换、Python 和 SymPy 以串联 RLC 电路为例简化电路分析的数学运算。

　　研究电路可能是一个非常滑坡。 在不知不觉中，你已经深入微分方程了。 对于那些对微积分感到不舒服的人来说，这可能是可怕的。 然而，我经常告诉我的EE学生，成为一名工程师并不是要善于以困难的方式解决难题; 相反，它主要是关于找到更简单的方法来解决这些问题。 当我教授电路分析课程并需要激励他们学习
拉普拉斯变换。

　　将随时间变化的微分方程转换为拉普拉斯空间可确保将这些微分方程的解简化为代数练习; 不需要微积分！ 然而，有时确定解决方案所涉及的代数量可能会抵消该方法的好处，使学生希望他们正在做更高级的数学。 然而，一种解决方案是
蟒。 利用Python可以大大减少确定解决方案所需的代数量。

　　在本文中，我们将首先通过一个例子，展示拉普拉斯空间是如何发挥作用的，以及 Python 如何帮助更轻松地完成数学。

　　示例：查找串联RLC电路中的电流

　　在进入拉普拉斯空间和Python如何在电路分析中发挥作用之前，让我们将示例设置到拉普拉斯变换进入的位置。

　　首先，考虑电流如何流过 电容器 与该电容器两端的电压与时间有关的导数成正比。 同样，两端的电压 感应器
与流过该电感器的电流与时间有关的导数成正比：

v_L = L\\frac{di_L}{dt}

等式 1a.

i_C = C \\frac{dv_C}{dt}

等式 1b.

　　这些差分关系对于描述和分析电路中的电流和电压行为至关重要，如图1所示。

　　

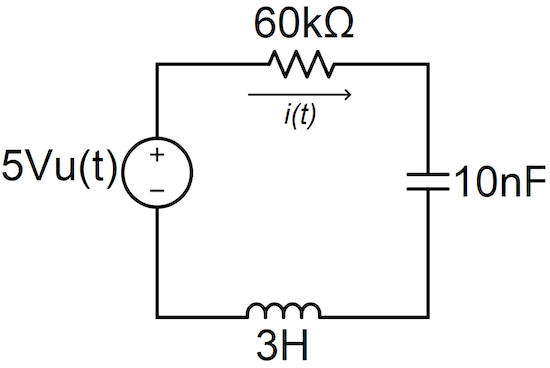
　　图1. RLC电路示例。

　　在 RLC电路 在图 1 中，我们看到流过元件的电流都是相等的，因为这些元件都是串联的。 此外，在t ≥ 0时，该电路无源元件两端的电压等于5V（直流电源电压）。 我们可以将这些关系写成等式 2 和 3。

　　iL=iC=iRiL=iC=iR等式 2.

　　vR+vL+vC=VdcvR+vL+vC=Vdca3.

　　将等式1a和1b与等式2和3相结合，得到等式4，这是一个积分微分方程，描述了流过图1所示电路的电流的时间行为。

u(t)5V=(3H)\\frac{di}{dt}+(60k\\Omega)i+\\bigg(\\frac{1}{10nF}\\bigg)\\int{idt}

　
等式4.

　　取公式4中关于时间的两边的导数，并重新排列微分项的系数，得到公式5，即描述图1电路中电流瞬态行为的微分方程。

\\frac{5V\\delta(t)}{3H}=\\frac{d^2i}{dt^2}+\\bigg(\\frac{60k\\Omega}{3H}\\bigg)\\frac{di}{dt}+\\bigg(\\frac{1}{3H\\cdot10nF}\\bigg)i

等式5.

　　让我们停下来反思一下我们刚刚做了什么。 到目前为止，我们还没有真正需要做太多的微积分。 基本上，我们已经描述了该电路中随时间推移的电流演变，但我们还没有解决该电流的功能形式。 如果我们要在时域中进行，我们需要确定该电路是过阻尼、欠阻尼还是临界阻尼。 然后，为我们的解选择了一个一般形式，我们需要将该一般解及其导数应用边界条件，以确定解的一般形式的几个常数值。

　　如果我们停留在时域中，这是求解二阶电路中电流的最简单、最直接的方法。 但是，如果我们将方程6转换为拉普拉斯空间，我们可以避免时域的混乱（即大部分实际微积分）。

　　L{f（t）}=F（s）=∫∞0−f（t）e−stdtL{f（t）}=F（s）=∫0−∞f（t）e−stdt等式 6.

　　现在我们已经在示例中达到了这一点，让我们简要概述一下拉普拉斯空间。

　　拉普拉斯空间 - 拉普拉斯变换属性和对

　　在这一点上，根据您的教育背景（或您对大学课程的褪色记忆），您可能想知道，“什么是拉普拉斯空间？ 我将把更完整的描述留给数学家，但出于我们的目的，你可以把拉普拉斯空间想象成一个复杂的频域。 拉普拉斯空间中的函数包含有关随时间变化的丰富信息，可以使用简单的代数来操作这些信息来提取该时间信息。

　　单侧拉普拉斯变换通常根据公式6通过积分进行。 该方程定义了f（t），F（s）的拉普拉斯变换，作为f（t）和e乘积积分的结果-圣从 t = 0-到无穷大。 此外，根据公式7进行从s空间到时域的逆变换。

　　L−1{F（s）}=f（t）=12πj∫ε+j∞ε−j∞F（s）estdsL−1{F（s）}=f（t）=12πj∫ε−j∞ε+j∞F（s）estds等式7.

　　你总是可以执行这些积分从 s 空间变换到 t 空间，然后再变换回来，但积分是一种痛苦，逆拉普拉斯变换积分要求我们确保 ϵϵ
的值位于该积分的收敛区域内; 我们真的应该掸去我们复杂的分析技能，以正确执行这个积分。 幸运的是，拉普拉斯变换和逆变换通常可以使用拉普拉斯空间的线性属性表和引用变换对表来执行，而无需完全积分。

　　图2a和2b显示了这些的最小版本，尽管可以通过互联网搜索找到更完整的拉普拉斯表。

　　

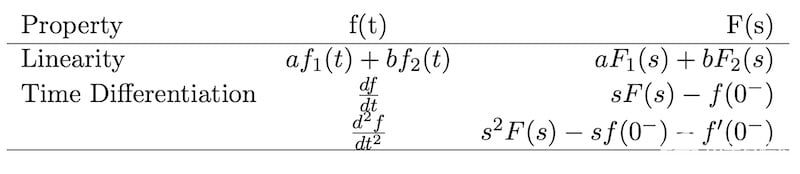
　　图 2a. 拉普拉斯变换属性。

　　

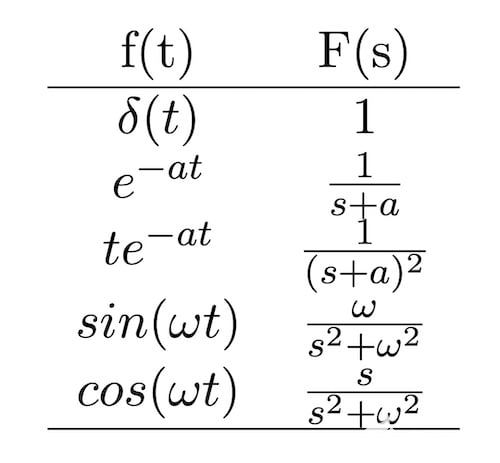
　　图 2b. 拉普拉斯变换对。

　　现在我们已经有了复习，让我们回到我们的示例。

　　求解拉普拉斯空间中的电流

　　将拉普拉斯变换属性应用于时间相关方程 6 的每个项，可得出 s 空间方程 8。 重要的是要注意，我在这里假设t =
0之前的电流是0A，并且已经有一段时间了。

s^2I(s)+\\bigg(\\frac{60k\\Omega}{3H}\\bigg)sI(s)+\\bigg(\\frac{1}{3H\\cdot10nF}\\bigg)I(s)=\\frac{5V}{3H}

等式8.

　　考虑到这一点，我们可以轻松地代数操作方程9以找到I（s）。 然后，确定 i（t） 就像逆变换 I（s）一样简单。 这种简单性是我们在拉普拉斯空间中进行电路分析的原因; 这是解决难题的一种非常快速的方法。

I(s) = \\bigg(\\frac{5V}{3H}\\bigg)\\bigg(\\frac{1}{s^2+\\big(\\frac{60k\\Omega}{3H}\\big)s+\\big(\\frac{1}{3H\\cdot10nF}\\big)}\\bigg)

等式9.

　　从这里开始，事情可能会变得有点混乱。 的确，我们可以通过反转用于使用图 2 中的表从时域转换到 s 空间的过程来执行逆变换。 但是，我们需要代数操作I（s） 的表达式，直到它符合图 2b中变换对表中的一个或许多函数的总和。 如果手工完成，这个过程可能涉及如此繁琐的代数，以至于它完全否定了在拉普拉斯空间中求解电路而不是求解时域微分方程的好处。

　　使用 Python 和 SymPy 执行逆拉普拉斯变换

　　在我们的示例中，我们已经手动完成了所有实际电路工作。 是时候拿出 Python 的计算能力了 SymPy 为我们做逆变换。

　　首先，我们需要打开一个 Python 环境。 我使用 谷歌合作实验室为了解决这些问题，因为它是基于Web的，我需要的所有库都可用，并且它会在命令旁边呈现任何可视输出。 该程序类似于 木星笔记本，但它是由谷歌维护的。

　　第 1 步，我们将导入 SymPy 库并定义我们的符号 — s 和 t：

　from sympy import *

s,t = symbols(‘s,t’)

　　考虑等式 9，我们可以用符号 ‘s’ 来定义 I（s）：

　i = 5/(3*(s**2 + 20000*s + 33333333))

　　最后，我们将I（s）逆变换到时域，并使用以下命令将结果打印到笔记本上：

inverse_laplace_transform(i, s, t).simplify()

　　然后生成公式 10：

\\frac{5\\sqrt{66666667}(e^{2\\sqrt{66666667}t}-1)e^{-t(\\sqrt{66666667}+10000)}\\theta(t)}{400000002}

等式10.

　　请注意，Heaviside 阶跃函数在此表达式中表示为 θ（t）。 等式 10 不是我们想要的形式，因为 SymPy试图保持分数表示而不是四舍五入无理数。 但是，只需在纸上稍作操作，我们可以将 i（t） 重写为等式 11：

　　
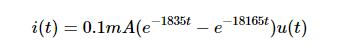
等式 11.

　　其中 u（t） 表示阶跃函数。

　　完成所有这些操作后，我们就完成了。 使用这个例子，这就是如何在 Python 和 SymPy 库的帮助下，使用 Laplace空间在二阶电路中求解未知的、随时间变化的量。

　　Python 还能如何帮助电路分析？

　　虽然本文的范围仅限于使用 Python 在分析二阶电路时执行逆拉普拉斯变换，但 Python 中的 SymPy库可用于帮助解决许多类型的电路分析问题。 每当涉及代数时，您都可以使用Python来减轻乏味。 我认为，最好的方法是应用所有必要的电路原理（基尔霍夫定律，欧姆定律等）用手。 然后，当您将问题简化为纸上的方程或方程组时，使用 Python完成该过程。 拉普拉斯空间中的电路分析是一个充分展示这种方法优势的舞台。 通过使用计算机执行逆变换，我们可以大大减少获得解决方案所需的手动代数操作量，并保留拉普拉斯空间的美丽和好处。