了解精密数模转换器中的温度漂移

本应用笔记分析了给精密数模转换器（DAC）带来误差的外部影响。重点将放在温度漂移上。此错误被识别为DAC误差预算的一部分。本文讨论了数据转换器和基准电压源引入的误差因素。在了解误差来源后，它提供了指定数据转换器所需的计算，这将补偿误差并满足系统的目标规格。

      本应用笔记重点介绍Maxim的3端基准电压源和精密DAC。基准电压源和DAC有许多规格，但仅讨论与误差预算相关的规格。

概述

理想的数模转换器（DAC）产生的模拟输出电压或电流完全线性，不受温度等许多外部影响的影响。也就是说，DAC当然会受到许多外部因素（特别是温度）引起的误差的影响。随着温度的变化，DAC可能会漂移。当使用精密DAC设置精确的偏置值时，这一点尤为重要。任何误差都可以在室温下校准。然而，随温度的变化更难补偿。随温度漂移最大的误差主要由失调误差和增益误差决定。

本应用笔记描述了DAC失调和增益误差如何随温度变化。它展示了设计人员如何预测设计过程中的错误。一旦理解了这些知识，这些知识可用于确保系统在整个温度范围内满足其所需的规格。

失调和增益误差

如上所述，DAC性能受到许多误差源的影响，包括失调误差和增益误差。这些因素在DAC数据手册的“静态精度”部分指定。图1所示为MAX5134 16位、四通道DAC的示例。

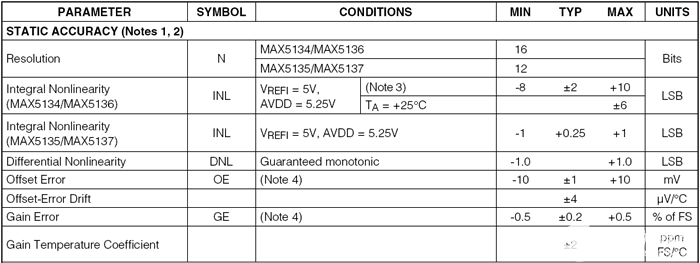
注4：增益和失调测试电压在GND和AVDD的100mV范围内。

       图1.MAX5134失调和增益误差

这些规格对DAC性能意味着什么？

失调误差定义了DAC的实际传递函数与单个点的理想值的匹配程度。对于单极性输出，这是代码零。此错误通常称为零代码错误。对于双极性输出，这是DAC输出应通过零点。

增益误差是传递函数斜率的量度。在示例设备中，斜率可以介于理想值的 99.5% 和 100.5% 之间。

理想的失调和增益误差如图2所示。请注意，失调和增益误差可以是正误差，也可以是负误差。

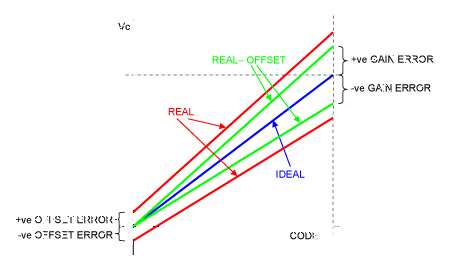
图2.失调和增益误差。

失调和增益误差通常不直接测量。如果单极性器件出现负失调误差，则在代码零处进行测量将产生错误的结果。对此的解释其实很简单。理论上，对于负失调误差，输出在代码零处应为负。单极性DAC无法做到这一点，因为它通常只有一个正电源。因此，测量两点并计算失调和增益误差。一个点接近代码零，而另一个点接近或可能达到最大代码。例如，MAX5134在100mV接地和AVDD范围内进行测试;模拟电源电压如图1注4所述。

现在考虑温度的影响。失调和增益误差均随温度漂移。当DAC用于设置精确的偏置值时，这一点尤为重要。固定失调和增益误差可以使用各种技术进行校准。（参见应用笔记4494：“数据转换器系统中增益误差的校准方法”，了解一些想法。然而，校准温度漂移要复杂得多，因为必须首先测量温度，并根据温度应用可变补偿。

示例计算和典型结果

以MAX5134为例，我们可以计算出在大量器件上看到的最大静态误差。首先，我们需要定义一些方程，使我们能够计算误差的程度。

VOUT = N × G × (GE + GET) + OE + OET

 

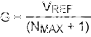
其中	V外= 输出电压
	N = DAC 代码
	G = DAC 增益
	GE = DAC 增益误差
	GET= 温度效应带来的额外增益误差
	OE = DAC 失调误差
	OET= 温度效应带来的额外失调误差
	VREF= 参考电压
	NMAX= 最大 DAC 代码

 

失调误差漂移的规格值为 ±4μV/°C。 这是使用 box 方法指定的。（参见应用笔记4300：“计算精密数模转换器（DAC）应用中的误差预算”，进一步说明。为了确定温度范围内的失调，我们将漂移乘以指定的温度范围。请注意，这是器件的指定工作范围，而不是应用的工作范围。在这种情况下，该范围为 -40°C 至 +105°C。 因此，温度范围内的失调漂移为±0.58mV。同样，增益温度系数指定为2ppm/°C，相当于总±0.029%FS（满量程）。

我们使用V裁判第一个例子是2.5V。在这种情况下，我们有一个 16 位 DAC，因此 N.MAX= 65535。

现在我们有一个小问题。失调和增益误差指定为“最小值/最大值”，这很有帮助。但是，温度效应仅指定为典型（典型）值。我们可以使用这些典型值，或者根据经验估计它们在所有批次中的变化。目前，我们只使用典型值。

如果我们绘制输出电压，包括初始误差与代码的关系，我们得到如图3所示的曲线。由于这是实际DAC的曲线，因此这些线之间的距离比图2中的要近得多。因此，最好绘制与理想的偏差。如图 4 所示。图4还显示了总误差，包括温度效应。

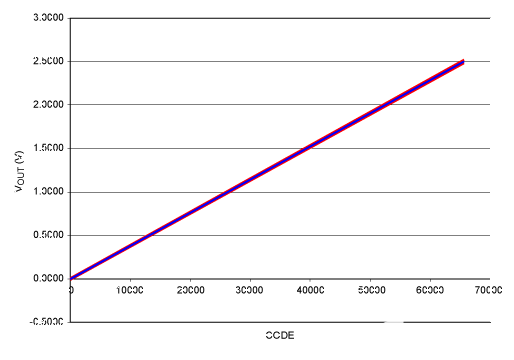
图3.DAC输出与代码的关系示例，显示增益和失调误差的范围，V裁判= 2.5V。

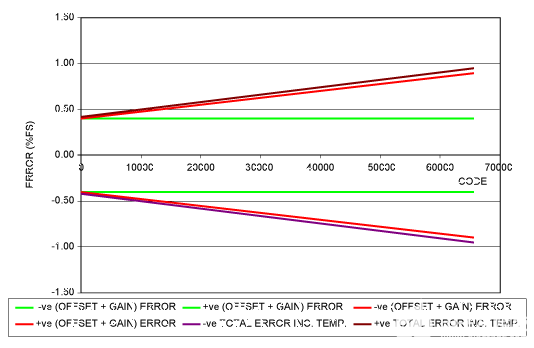
图4.DAC输出误差与DAC代码的关系示例，VREF= 2.5V。

我们立即看到温度效应比初始误差小得多。因此，即使数据手册仅规定了温度效应的典型值，总误差也不会因此而受到显著影响。代码零时的总误差为±0.423%FS （±10.6mV），最大代码时的总误差为±0.952%FS （±23.8mV）。

可能需要进行一些改进。如果基准电压增加，增益误差的绝对值将增加，因为它们被指定为%FS。但是，偏移误差在绝对值上将保持不变。因此，增加基准电压的效果是增加满量程电压。然后，我们可以在外部将DAC输出分压到所需的电压。这将有效地将增益误差分频回其原始值。但是，失调误差也会被划分。图 5 显示了这种方案的效果。

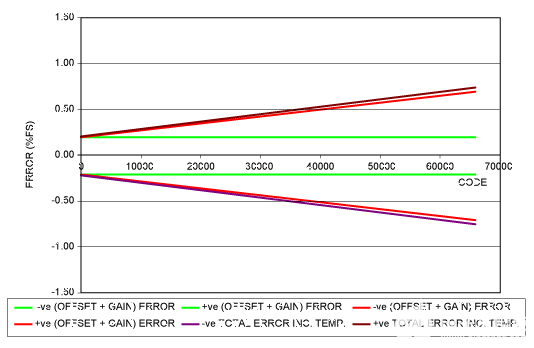
图5.DAC输出误差与DAC代码的关系示例，VREF= 2.5V。

代码零时的总误差为±0.212%FS （±5.3mV），最大代码时的总误差为±0.740%FS （±18.5mV）。

当然，我们忽略了输出分频器中涉及的任何错误。但是，这种方法是合理的，因为可以使用精密分压器。例如，MAX5490分压器在整个温度范围内可实现±0.05%的比率精度。当然，分割DAC输出的缺点是会失去驱动能力。这可以使用放大器恢复，但这会增加误差本身。关于这种策略的讨论超出了本应用说明的范围。

结论

我们定义了影响DAC的失调和增益误差。我们通过示例展示了如何计算将存在的最坏情况误差，并给出了一个典型示例。我们还提出了一种改善总误差的可能方法。

审核编辑：郭婷